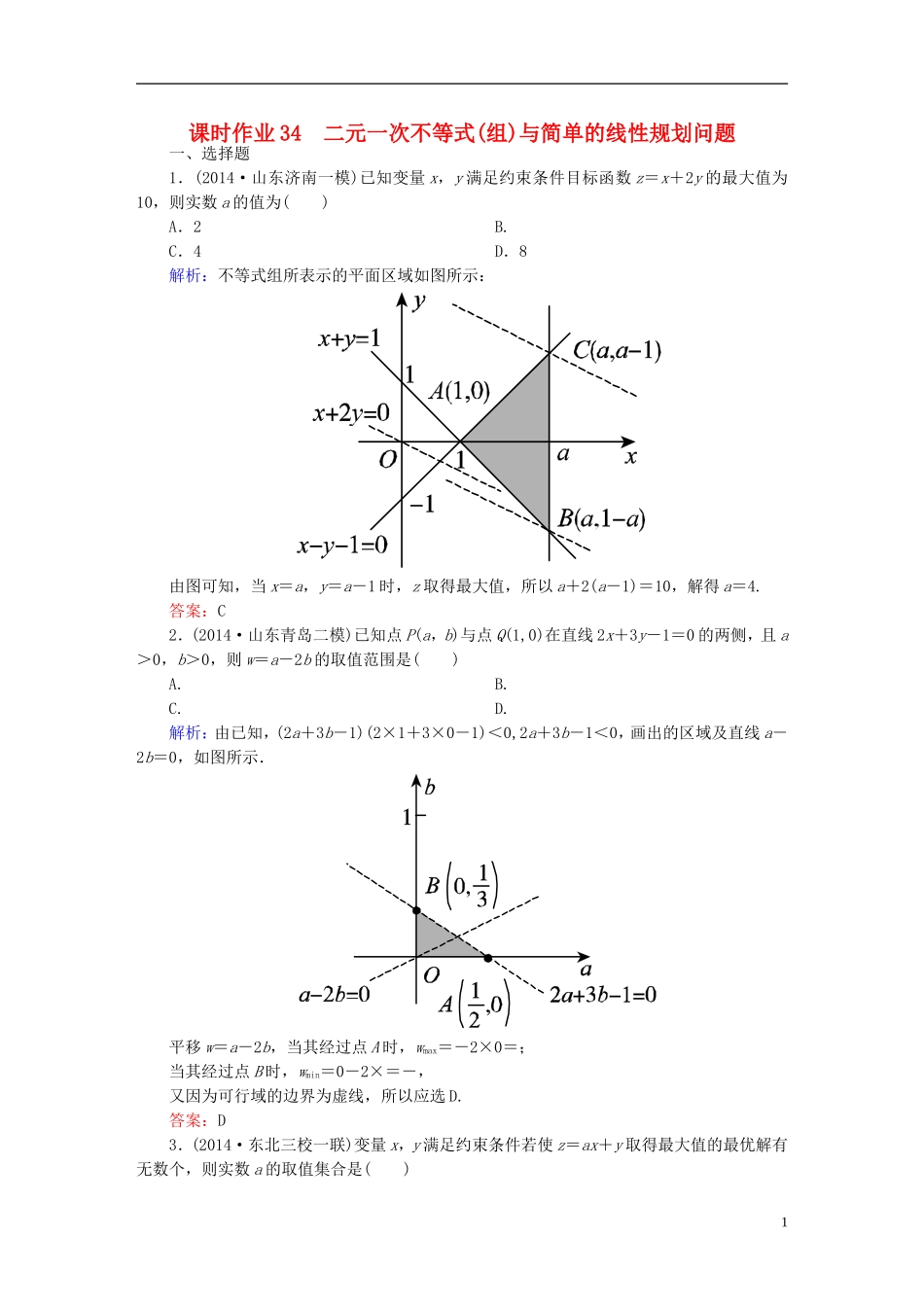
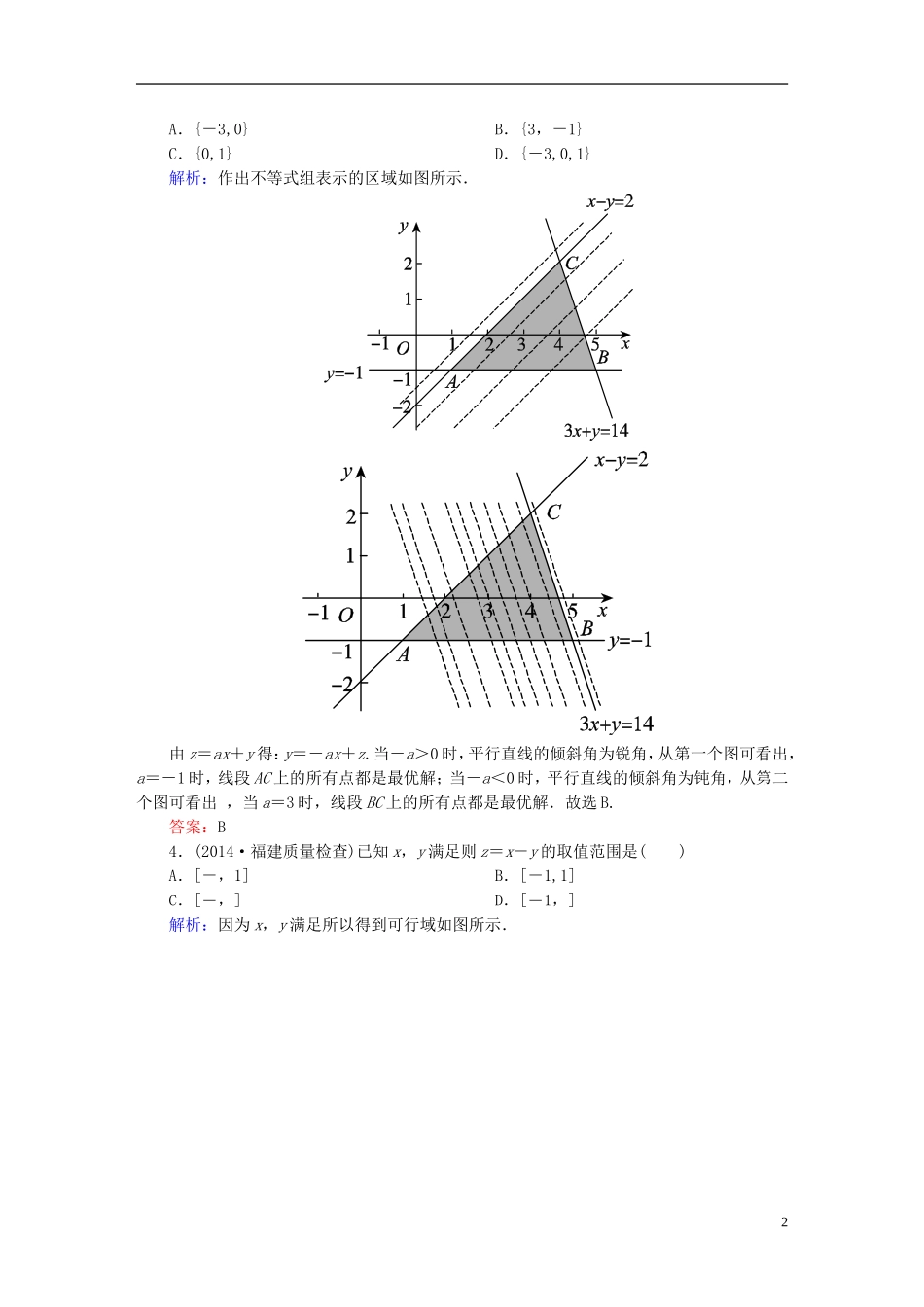
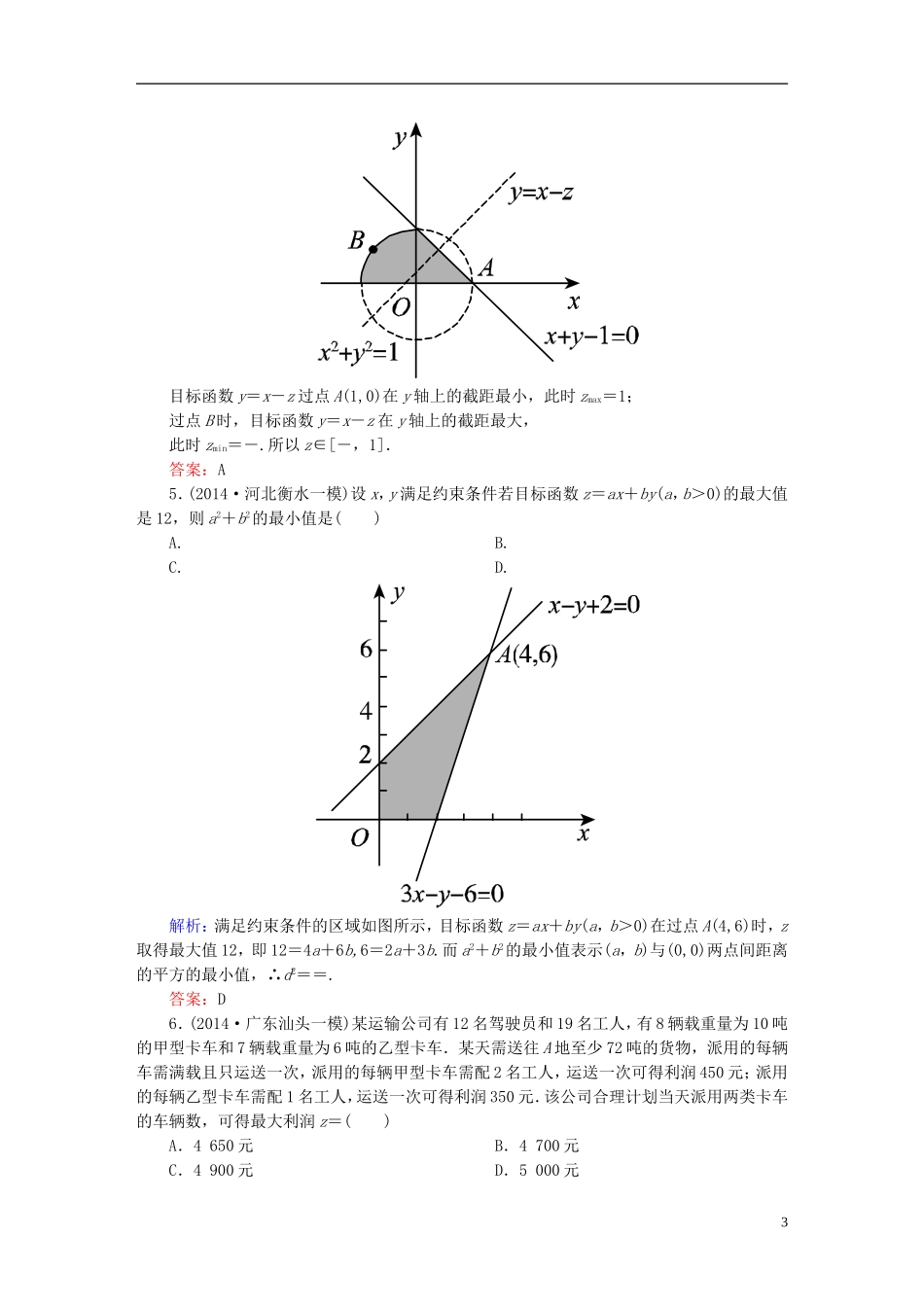
课时作业34二元一次不等式(组)与简单的线性规划问题一、选择题1.(2014·山东济南一模)已知变量x,y满足约束条件目标函数z=x+2y的最大值为10,则实数a的值为()A.2B.C.4D.8解析:不等式组所表示的平面区域如图所示:由图可知,当x=a,y=a-1时,z取得最大值,所以a+2(a-1)=10,解得a=4.答案:C2.(2014·山东青岛二模)已知点P(a,b)与点Q(1,0)在直线2x+3y-1=0的两侧,且a>0,b>0,则w=a-2b的取值范围是()A.B.C.D.解析:由已知,(2a+3b-1)(2×1+3×0-1)<0,2a+3b-1<0,画出的区域及直线a-2b=0,如图所示.平移w=a-2b,当其经过点A时,wmax=-2×0=;当其经过点B时,wmin=0-2×=-,又因为可行域的边界为虚线,所以应选D.答案:D3.(2014·东北三校一联)变量x,y满足约束条件若使z=ax+y取得最大值的最优解有无数个,则实数a的取值集合是()1A.{-3,0}B.{3,-1}C.{0,1}D.{-3,0,1}解析:作出不等式组表示的区域如图所示.由z=ax+y得:y=-ax+z.当-a>0时,平行直线的倾斜角为锐角,从第一个图可看出,a=-1时,线段AC上的所有点都是最优解;当-a<0时,平行直线的倾斜角为钝角,从第二个图可看出,当a=3时,线段BC上的所有点都是最优解.故选B.答案:B4.(2014·福建质量检查)已知x,y满足则z=x-y的取值范围是()A.[-,1]B.[-1,1]C.[-,]D.[-1,]解析:因为x,y满足所以得到可行域如图所示.2目标函数y=x-z过点A(1,0)在y轴上的截距最小,此时zmax=1;过点B时,目标函数y=x-z在y轴上的截距最大,此时zmin=-.所以z∈[-,1].答案:A5.(2014·河北衡水一模)设x,y满足约束条件若目标函数z=ax+by(a,b>0)的最大值是12,则a2+b2的最小值是()A.B.C.D.解析:满足约束条件的区域如图所示,目标函数z=ax+by(a,b>0)在过点A(4,6)时,z取得最大值12,即12=4a+6b,6=2a+3b.而a2+b2的最小值表示(a,b)与(0,0)两点间距离的平方的最小值,∴d2==.答案:D6.(2014·广东汕头一模)某运输公司有12名驾驶员和19名工人,有8辆载重量为10吨的甲型卡车和7辆载重量为6吨的乙型卡车.某天需送往A地至少72吨的货物,派用的每辆车需满载且只运送一次,派用的每辆甲型卡车需配2名工人,运送一次可得利润450元;派用的每辆乙型卡车需配1名工人,运送一次可得利润350元.该公司合理计划当天派用两类卡车的车辆数,可得最大利润z=()A.4650元B.4700元C.4900元D.5000元3解析:设派用甲型卡车x辆,乙型卡车y辆,则,目标函数z=450x+350y,画出可行域如图,当目标函数经过A(7,5)时,利润z最大,为4900元.答案:C二、填空题7.(2014·北京西城一模)若不等式组表示的平面区域是一个四边形,则实数a的取值范围是__________.解析:平面区域如图中的阴影部分,直线2x+y=6交x轴于点A(3,0),交直线x=1于点B(1,4),当直线x+y=a与直线2x+y=6在线段AB(不包括线段端点)时,此时不等式组所表示的区域是一个四边形.将点A的坐标代入直线x+y=a的方程得3+0=a,即a=3,将点B的坐标代入直线x+y=a的方程得a=1+4=5,故实数a的取值范围是(3,5).答案:(3,5)8.(2014·河北唐山一模)设变量x,y满足约束条件则目标函数z=3x-2y的最大值为__________.4解析:约束条件满足的区域如图所示,z=3x-2y,y=x-,要求z的最大值,即将直线y=x平移到B点处-最小,所以z最大,所以目标函数在点B(2,0)处取得最大值为6.答案:69.(2014·北京顺义一模)设x,y满足约束条件则目标函数z=的最小值为__________.解析:画出可行域,如图所示,z=表示可行域内的点到原点(0,0)的距离,由图得,距离的最小值为原点(0,0)到直线2x+y-2=0的距离d==.答案:三、解答题10.(2014·合肥模拟)画出不等式组表示的平面区域,并回答下列问题:(1)指出x,y的取值范围;(2)平面区域内有多少个整点?解析:(1)不等式x-y+5≥0表示直线x-y+5=0上及其右下方的点的集合,x+y≥0表示直线x+y=0上及其右上方的点的集合,x≤3表示直线x=3上及其左方的点的集合.5所以,不等式组表示的平面区域如图所示.结合图中可行域得x∈,y∈[-3,8].(2)由图形及不等...