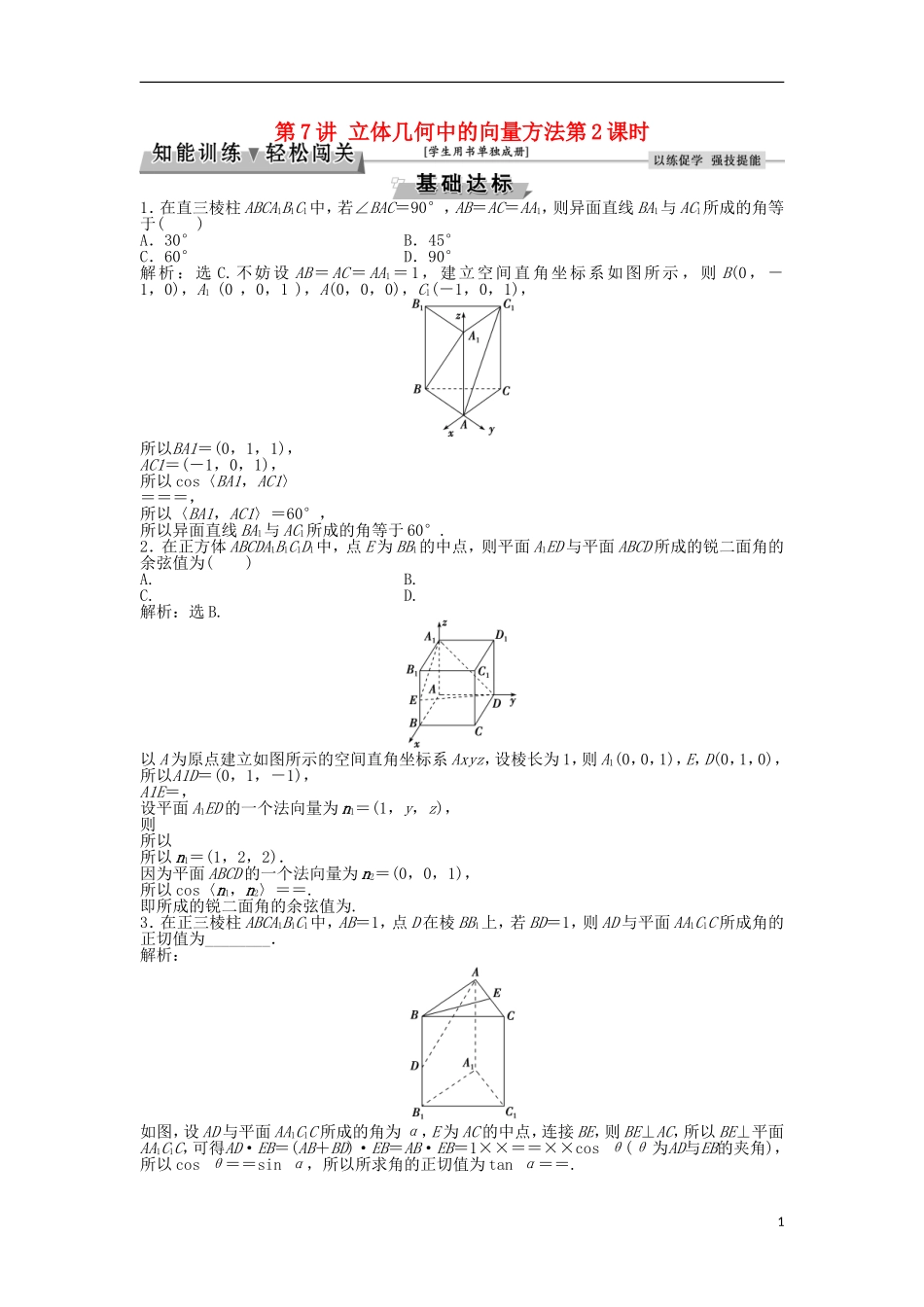
第7讲立体几何中的向量方法第2课时1.在直三棱柱ABCA1B1C1中,若∠BAC=90°,AB=AC=AA1,则异面直线BA1与AC1所成的角等于()A.30°B.45°C.60°D.90°解析:选C.不妨设AB=AC=AA1=1,建立空间直角坐标系如图所示,则B(0,-1,0),A1(0,0,1),A(0,0,0),C1(-1,0,1),所以BA1=(0,1,1),AC1=(-1,0,1),所以cos〈BA1,AC1〉===,所以〈BA1,AC1〉=60°,所以异面直线BA1与AC1所成的角等于60°.2.在正方体ABCDA1B1C1D1中,点E为BB1的中点,则平面A1ED与平面ABCD所成的锐二面角的余弦值为()A.B.C.D.解析:选B.以A为原点建立如图所示的空间直角坐标系Axyz,设棱长为1,则A1(0,0,1),E,D(0,1,0),所以A1D=(0,1,-1),A1E=,设平面A1ED的一个法向量为n1=(1,y,z),则所以所以n1=(1,2,2).因为平面ABCD的一个法向量为n2=(0,0,1),所以cos〈n1,n2〉==.即所成的锐二面角的余弦值为.3.在正三棱柱ABCA1B1C1中,AB=1,点D在棱BB1上,若BD=1,则AD与平面AA1C1C所成角的正切值为________.解析:如图,设AD与平面AA1C1C所成的角为α,E为AC的中点,连接BE,则BE⊥AC,所以BE⊥平面AA1C1C,可得AD·EB=(AB+BD)·EB=AB·EB=1××==××cosθ(θ为AD与EB的夹角),所以cosθ==sinα,所以所求角的正切值为tanα==.1答案:4.如图所示,在空间直角坐标系中有直三棱柱ABCA1B1C1,CA=CC1=2CB,则直线BC1与直线AB1夹角的余弦值为________.解析:不妨令CB=1,则CA=CC1=2,可得O(0,0,0),B(0,0,1),C1(0,2,0),A(2,0,0),B1(0,2,1),所以BC1=(0,2,-1),AB1=(-2,2,1),所以cos〈BC1,AB1〉====>0.所以BC1与AB1的夹角即为直线BC1与直线AB1的夹角,所以直线BC1与直线AB1夹角的余弦值为.答案:5.已知单位正方体ABCDA1B1C1D1,E,F分别是棱B1C1,C1D1的中点.试求:(1)AD1与EF所成角的大小;(2)AF与平面BEB1所成角的余弦值.解:建立如图所示的空间直角坐标系,得A(1,0,1),B(0,0,1),D1(1,1,0),E,F.(1)因为AD1=(0,1,-1),EF=,所以cos〈AD1,EF〉==,即AD1与EF所成的角为60°.(2)FA=,由图可得,BA=(1,0,0)为平面BEB1的一个法向量,设AF与平面BEB1所成的角为θ,则sinθ=|cos〈BA,FA〉|==,所以cosθ=.即AF与平面BEB1所成角的余弦值为.6.(2015·高考重庆卷)如图,三棱锥PABC中,PC⊥平面ABC,PC=3,∠ACB=.D,E分别为线段AB,BC上的点,且CD=DE=,CE=2EB=2.(1)证明:DE⊥平面PCD;(2)求二面角APDC的余弦值.解:(1)证明:由PC⊥平面ABC,DE平面ABC,得PC⊥DE.由CE=2,CD=DE=,得△CDE为等腰直角三角形,故CD⊥DE.由PC∩CD=C,DE垂直于平面PCD内两条相交直线,故DE⊥平面PCD.(2)由(1)知,△CDE为等腰直角三角形,∠DCE=.如图,过D作DF垂直CE于F,易知DF=FC2=FE=1.又已知EB=1,故FB=2.由∠ACB=,得DF∥AC,==,故AC=DF=.以C为坐标原点,分别以CA,CB,CP的方向为x轴,y轴,z轴的正方向建立空间直角坐标系,则C(0,0,0),P(0,0,3),A,E(0,2,0),D(1,1,0),ED=(1,-1,0),DP=(-1,-1,3),DA=.设平面PAD的法向量为n1=(x1,y1,z1),由n1·DP=0,n1·DA=0,得故可取n1=(2,1,1).由(1)可知DE⊥平面PCD,故平面PCD的法向量n2可取为ED,即n2=(1,-1,0),从而法向量n1,n2的夹角的余弦值为cos〈n1,n2〉==,故所求二面角APDC的余弦值为.1.(2016·山西省考前质量检测)如图,四棱锥PABCD中,底面ABCD为梯形,PD⊥底面ABCD,AB∥CD,AD⊥CD,AD=AB=1,BC=.(1)求证:平面PBD⊥平面PBC;(2)设H为CD上一点,满足CH=2HD,若直线PC与平面PBD所成的角的正切值为,求二面角HPBC的余弦值.解:(1)证明:由AD⊥CD,AB∥CD,AD=AB=1,可得BD=.又BC=,所以CD=2,所以BC⊥BD.因为PD⊥底面ABCD,所以PD⊥BC,又PD∩BD=D,所以BC⊥平面PBD,又BC平面PBC,所以平面PBD⊥平面PBC.(2)由(1)可知∠BPC为PC与平面PBD所成的角,所以tan∠BPC=,所以PB=,PD=1.由CH=2HD及CD=2,可得CH=,DH=.以点D为坐标原点,DA,DC,DP所在直线分别为x轴,y轴,z轴建立空间...