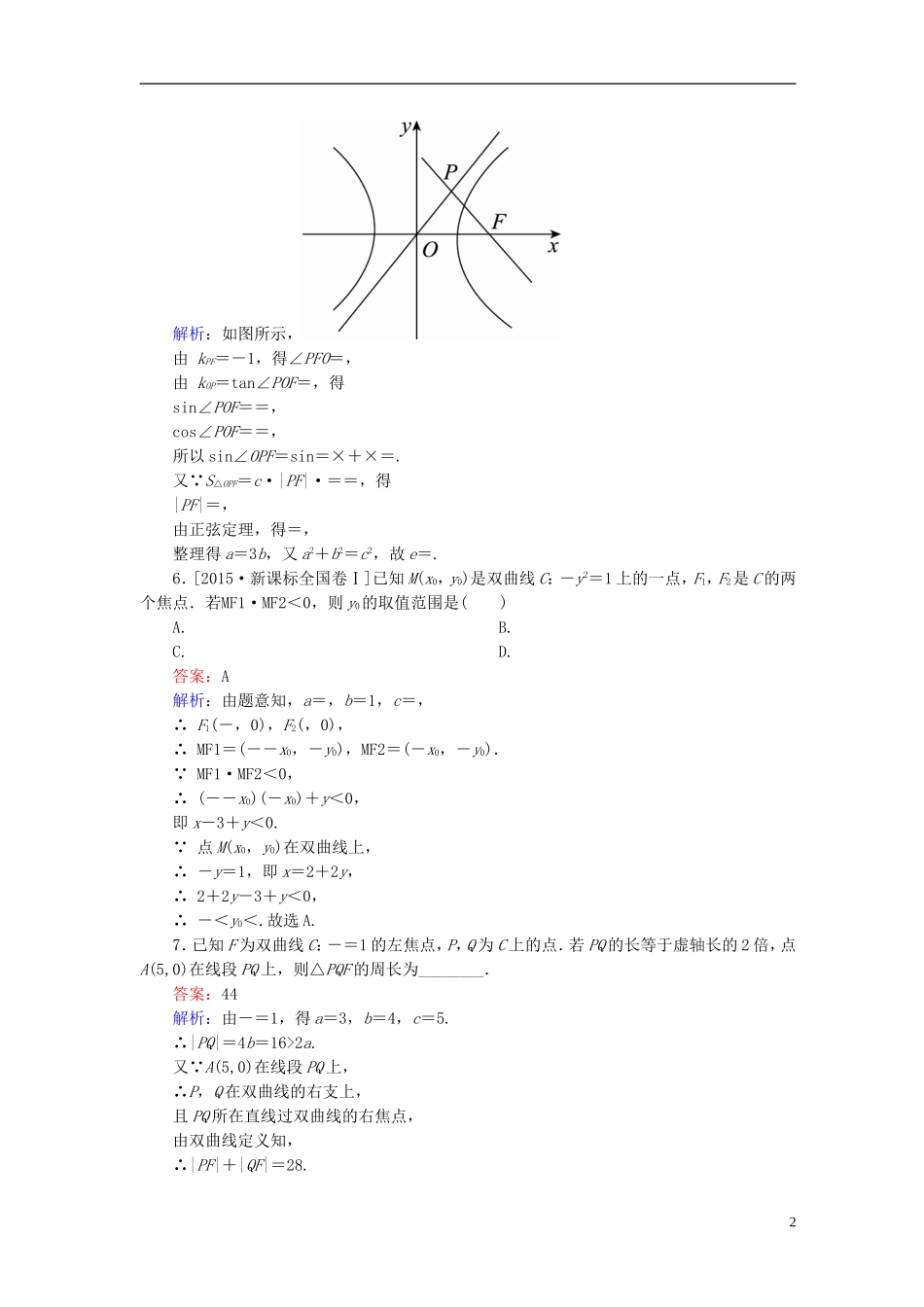
课时跟踪检测(五十二)[高考基础题型得分练]1.双曲线x2-my2=1的实轴长是虚轴长的2倍,则m=()A.B.C.2D.4答案:D解析:双曲线的方程可化为x2-=1,∴实轴长为2,虚轴长为2,∴2=2×2,解得m=4.2.已知双曲线C的渐近线方程为y=±2x,且经过点(2,2),则C的方程为()A.-=1B.-=1C.-=1D.-=1答案:A解析:由题意,设双曲线C的方程为-x2=λ(λ≠0),因为双曲线C过点(2,2),则-22=λ,解得λ=-3,所以双曲线C的方程为-x2=-3,即-=1.3.[2017·吉林长春模拟]已知F1,F2是双曲线-=1(a>0,b>0)的两个焦点,以F1F2为直径的圆与双曲线的一个交点是P,且△F1PF2的三条边长成等差数列,则此双曲线的离心率是()A.B.C.2D.5答案:D解析:不妨设点P位于第一象限,F1为左焦点,|PF2|=m-d,|PF1|=m,|F1F2|=m+d,其中m>d>0,则有(m-d)2+m2=(m+d)2,解得m=4d,故双曲线的离心率e==5.4.若双曲线x2+=1的一条渐近线的倾斜角α∈,则m的取值范围是()A.(-3,0)B.(-,0)C.(0,3)D.答案:A解析:由题意可知m<0,双曲线的标准方程为x2-=1,经过第一、三象限的渐近线方程为y=x,因为其倾斜角α∈,所以=tanα∈(0,),故m∈(-3,0).5.[2017·河南郑州模拟]已知双曲线-=1(a>0,b>0)的右焦点为F,过F作斜率为-1的直线交双曲线的渐近线于点P,点P在第一象限,O为坐标原点,若△OFP的面积为,则该双曲线的离心率为()A.B.C.D.答案:C1解析:如图所示,由kPF=-1,得∠PFO=,由kOP=tan∠POF=,得sin∠POF==,cos∠POF==,所以sin∠OPF=sin=×+×=.又 S△OPF=c·|PF|·==,得|PF|=,由正弦定理,得=,整理得a=3b,又a2+b2=c2,故e=.6.[2015·新课标全国卷Ⅰ]已知M(x0,y0)是双曲线C:-y2=1上的一点,F1,F2是C的两个焦点.若MF1·MF2<0,则y0的取值范围是()A.B.C.D.答案:A解析:由题意知,a=,b=1,c=,∴F1(-,0),F2(,0),∴MF1=(--x0,-y0),MF2=(-x0,-y0). MF1·MF2<0,∴(--x0)(-x0)+y<0,即x-3+y<0. 点M(x0,y0)在双曲线上,∴-y=1,即x=2+2y,∴2+2y-3+y<0,∴-<y0<.故选A.7.已知F为双曲线C:-=1的左焦点,P,Q为C上的点.若PQ的长等于虚轴长的2倍,点A(5,0)在线段PQ上,则△PQF的周长为________.答案:44解析:由-=1,得a=3,b=4,c=5.∴|PQ|=4b=16>2a.又 A(5,0)在线段PQ上,∴P,Q在双曲线的右支上,且PQ所在直线过双曲线的右焦点,由双曲线定义知,∴|PF|+|QF|=28.2∴△PQF的周长是|PF|+|QF|+|PQ|=28+16=44.8.已知F1,F2是双曲线-=1(a>0,b>0)的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点P在双曲线上,则双曲线的离心率是________.答案:+1解析:因为MF1的中点P在双曲线上,|PF2|-|PF1|=2a,△MF1F2为正三角形,边长都是2c,所以c-c=2a,所以e===+1.9.过双曲线C:-=1(a>0,b>0)的右焦点作一条与其渐近线平行的直线,交C于点P.若点P的横坐标为2a,则C的离心率为________.答案:2+解析:如图,F1,F2为双曲线C的左,右焦点,将点P的横坐标2a代入-=1中,得y2=3b2,不妨令点P的坐标为(2a,-b),此时kPF2==,得到c=(2+)a,即双曲线C的离心率e==2+.10.[2017·江南十校联考]已知双曲线的中心在原点,焦点F1,F2在坐标轴上,离心率为,且过点P(4,-).(1)求双曲线的方程;(2)若点M(3,m)在双曲线上,求证:MF1·MF2=0.(1)解: e=,∴可设双曲线的方程为x2-y2=λ(λ≠0). 双曲线过点(4,-),∴16-10=λ,即λ=6.∴双曲线的方程为x2-y2=6.(2)证明:证法一:由(1)可知,a=b=,∴c=2,∴F1(-2,0),F2(2,0),∴kMF1=,kMF2=,kMF1·kMF2==-. 点M(3,m)在双曲线上,∴9-m2=6,m2=3,故kMF1·kMF2=-1,∴MF1⊥MF2.∴MF1·MF2=0.证法二:由(1)可知,a=b=,∴c=2,∴F1(-2,0),F2(2,0),MF1=(-2-3,-m),MF2=(2-3,-m),3∴MF1·MF2=(3+2)×(3-2)+m2=-3+m2, 点M(3,0)在双曲线上,∴9-m2=6,即m2-3=0,∴MF1·MF2=0.[冲刺名校能力提升练]1.如图,F1,F2是椭圆C1:+y...