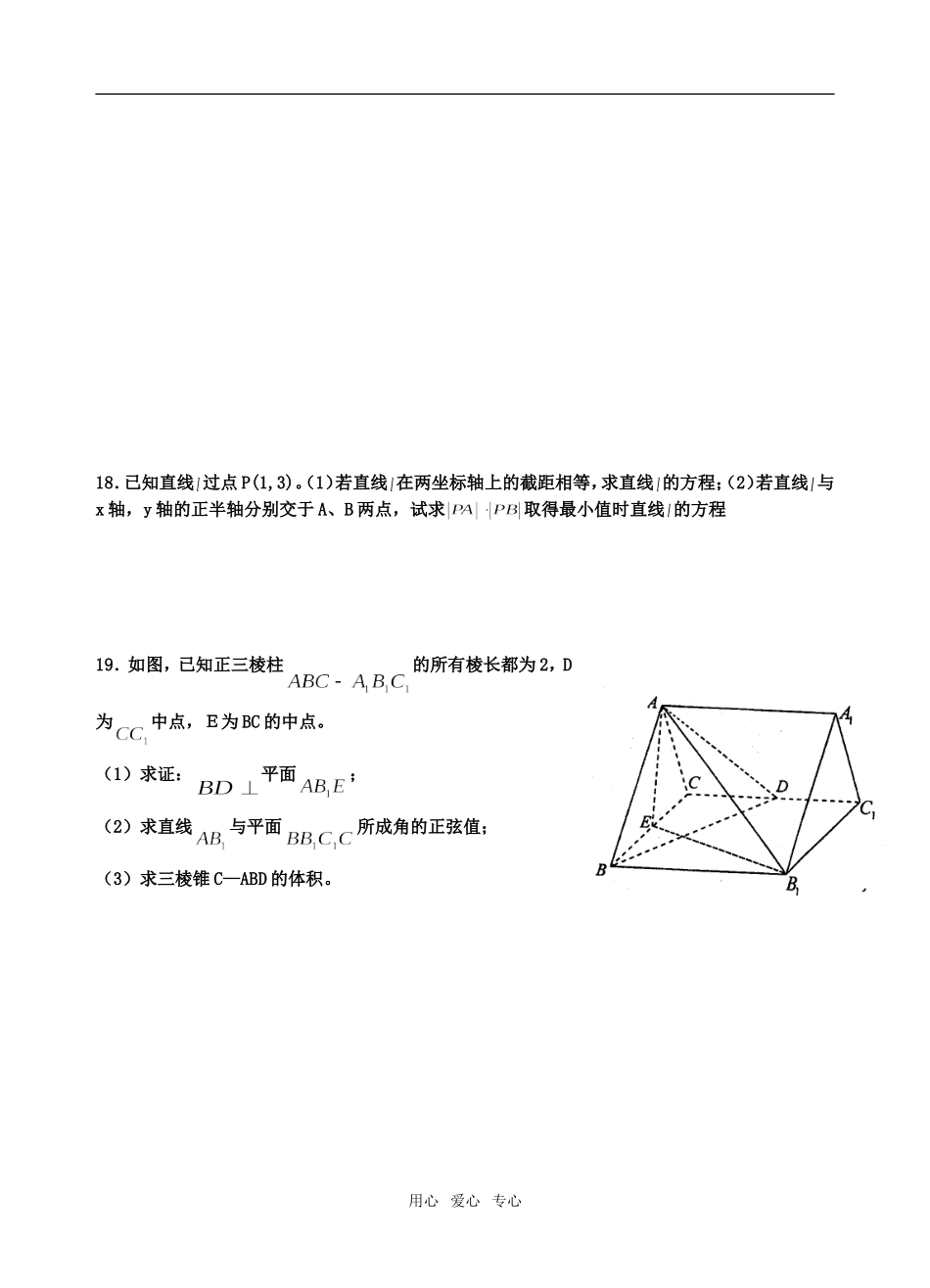
2-①2-②a震川中学高二数学练习71.已知正三棱锥P—ABC中,侧棱,D、E分别是侧棱PB、PC上的点,则的周长的最小值是;2.若过点和的直线与直线平行,则=.3.一个长方体的各顶点均在同一个球的球面上,且过同一个顶点的三条棱的长分别为1,2,3,则此球的表面积是;4.直线经过一定点,则此点是5.已知正四棱锥P—ABCD的主视图和左视图均为边长是2的正三角形,俯视图是边长为2的正方形,则此正四棱锥的体积是;6.已知为两条不同的直线,为两个不同的平面,给出如下命题:(1)若,则;(2)若,则;(3)若,则;(4)若则。其中正确命题的序号是;7.如图所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为.8.已知两个球的表面积之比为1∶,则这两个球的半径之比为.9.直线与平行,则的值为;10.若圆锥的高是底面半径和母线的等比中项,则称此圆锥为“黄金圆锥”,已知某黄金圆锥的侧面积为,则这个圆锥的高为_________________。11.如图为一几何体的展开图,其中四边形ABCD是边长为6的正方形,SD=PD=6,CR=CS,AQ=AP,点S、D、A、Q及P、D、C、R分别共线,沿图中虚线将它们折叠起来,使P、Q、R、S四点重合,则需要________个这样的几何体可以拼成一个棱长为6的正方体。12.直线:关于直线:对称的直线的方程为。13.点是直线上的动点,则代数式的最小值为______________。14.如图,一个圆锥形容器的高为,内装有一定量的水.用心爱心专心主视图左视图俯视图CAPRBDSQDBCAO1xy如果将容器倒置,这时所形成的圆锥的高恰为(如图2-②),则图2-①中的水面高度为.15.如图,在平行四边形中,点.(1)求所在直线的斜率;(2)过点C做CD⊥AB于点D,求所在直线的方程.16.已知直线与,则当为何值时,直线:(1)平行?(2)垂直?(3)相交且交点在轴上方?17.如图,三棱锥中,是边长为4的正三角形,,E为AB的中点,.(Ⅰ)求证:平面;(Ⅱ)求直线和平面CDE所成的角的正切;(Ⅲ)求点A到平面BCD的距离.用心爱心专心18.已知直线过点P(1,3)。(1)若直线在两坐标轴上的截距相等,求直线的方程;(2)若直线与x轴,y轴的正半轴分别交于A、B两点,试求取得最小值时直线的方程19.如图,已知正三棱柱的所有棱长都为2,D为中点,E为BC的中点。(1)求证:平面;(2)求直线与平面所成角的正弦值;(3)求三棱锥C—ABD的体积。用心爱心专心20.如图,已知四棱锥P-ABCD的底面ABCD为等腰梯形,AB∥DC,AC⊥BD,AC与BD相交于点O,且顶点P在底面上的射影恰为O点,又BO=2,PO=,PB⊥PD.(Ⅰ)求异面直线PD与BC所成角的余弦值;(Ⅱ)求二面角P-AB-C的大小;(Ⅲ)设点M在棱PC上,且为何值时,PC⊥平面BMD.震川中学高二数学练习7一、填空题(本大题共14小题,每小题5分,共70分).1.2.3.244.5.6.7.8.1:39.或10.。11.12.13.614.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)15.(本题满分14分)解:(1)点O(0,0),点C(1,3),OC所在直线的斜率为.(2)在中,,CD⊥AB,CD⊥OC.CD所在直线的斜率为.CD所在直线方程为.用心爱心专心DBCAO1xy16.(Ⅰ)由,得(Ⅱ)由得(Ⅲ)由,消去得即,∴17.((1)略证:;(2)作AF⊥DE于F点,可证AF长即为所求,AD=3,AE=2,,,;(3)等体积法:BD=DC=5,BC=4,,,,。18.设截距相等的直线方程为或,……………………………………3∵直线过点P(1,3),得a=4,k=3…………………………………………..6所求直线方程为,或……………………………………….8(若只考虑一种情况,得4分)(2)根据题意得直线的斜率存在∴可设直线的方程为y-3=k(x-1)(k<0),可求得A(o,3-k),;等号当且仅当时等号成立,此时k=-1,直线的方程为y-3=-(x-1)即y=-x+419.(Ⅰ)∵棱柱是正三棱柱,且E为BC的中点,∴平面平面,又,∴,而用心爱心专心为中点,且,∴由棱长全相等知,即,故又,∴;(Ⅱ)由知是直线与平面所成的角,设为θ∵正三棱柱的所有棱长都为∴在中(Ⅲ)20.(1),DO=1,取AB中点E,连DE,故DE//BC,连PE,故(或其补角)为异面直线PD与BC所成角,,。(2)连OE,PE,可证得为二面角P-AB-C的平面角,,。(3),。若面BMD,则,,,。用心爱心专心