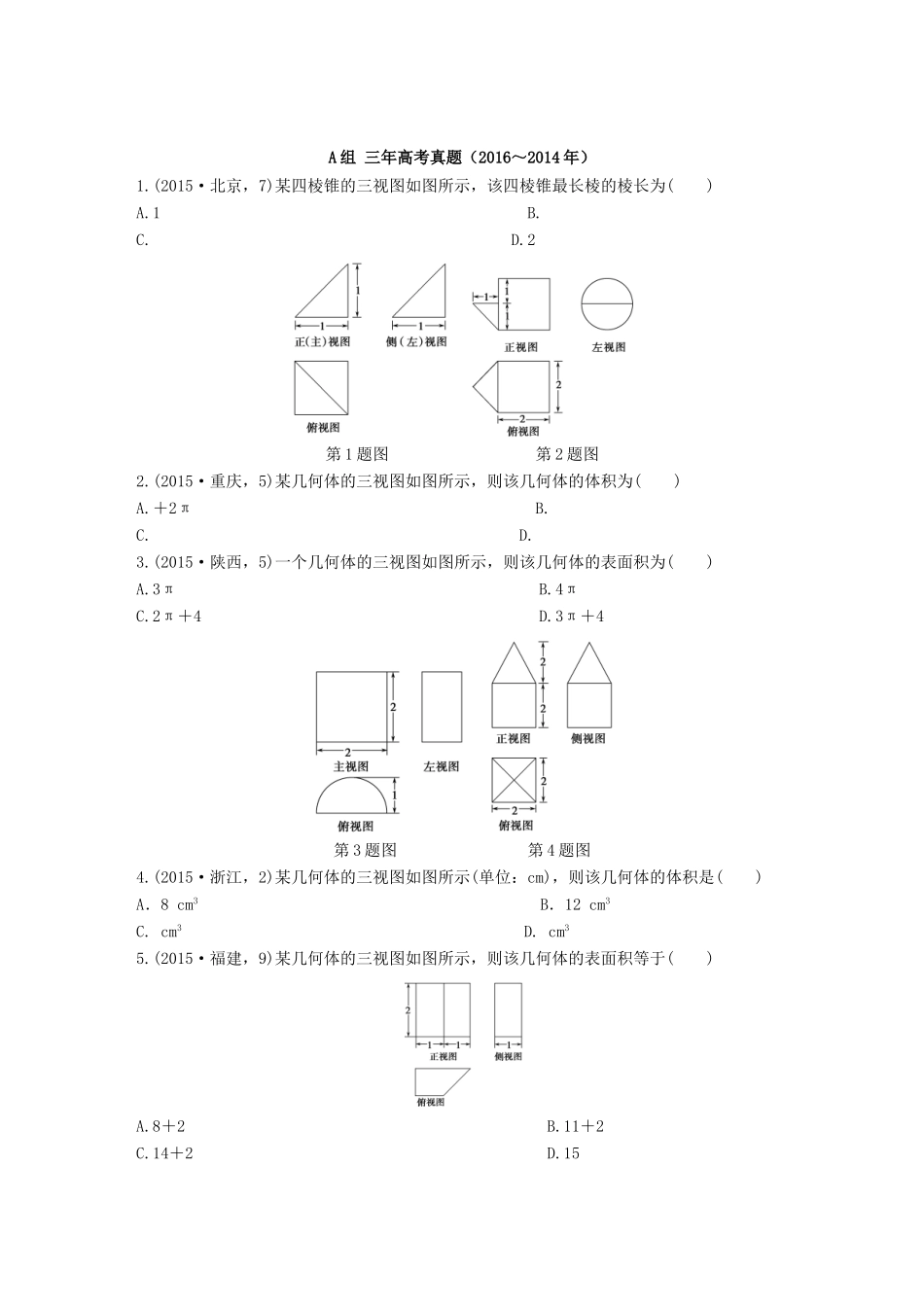
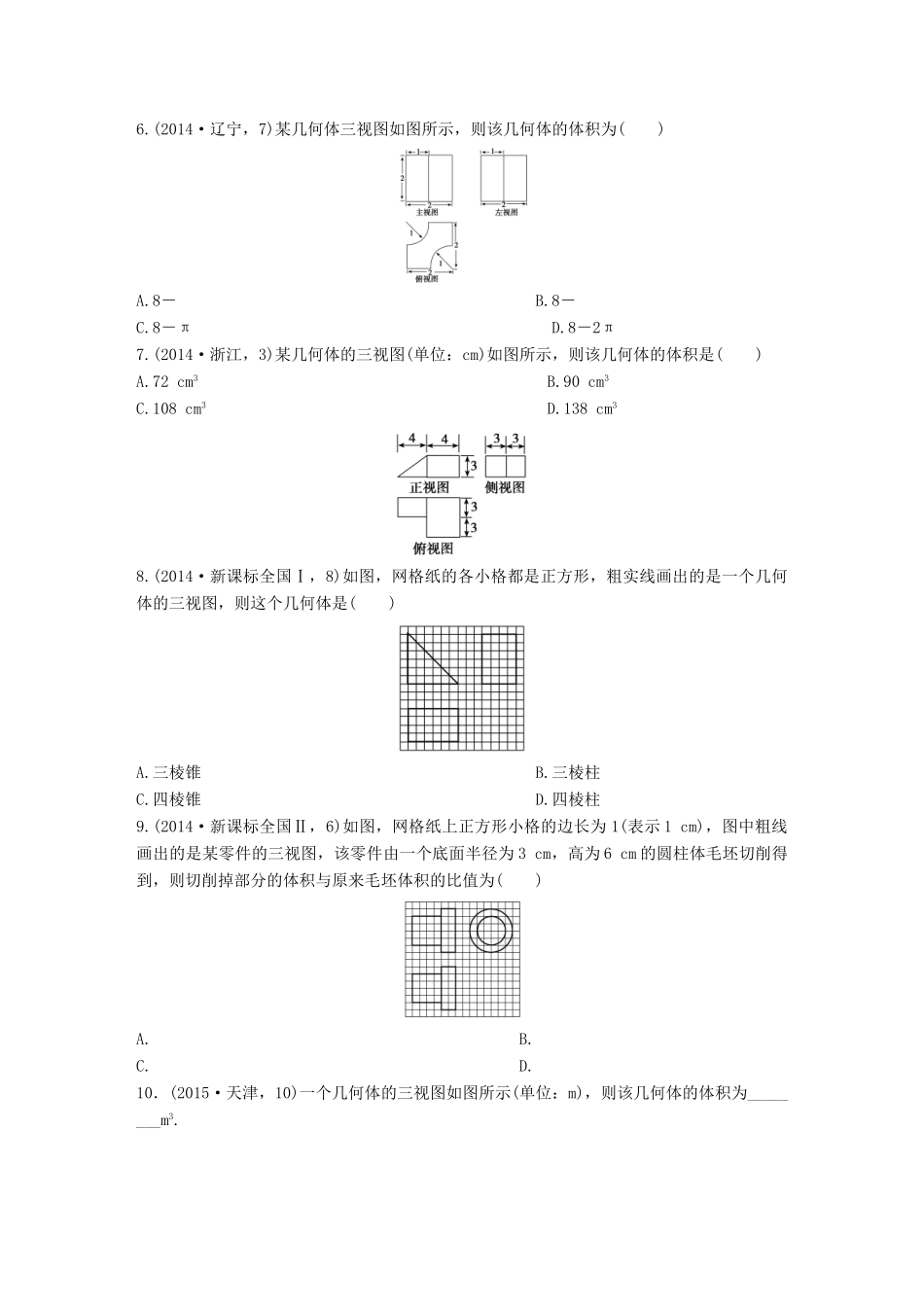
A组三年高考真题(2016~2014年)1.(2015·北京,7)某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为()A.1B.C.D.2第1题图第2题图2.(2015·重庆,5)某几何体的三视图如图所示,则该几何体的体积为()A.+2πB.C.D.3.(2015·陕西,5)一个几何体的三视图如图所示,则该几何体的表面积为()A.3πB.4πC.2π+4D.3π+4第3题图第4题图4.(2015·浙江,2)某几何体的三视图如图所示(单位:cm),则该几何体的体积是()A.8cm3B.12cm3C.cm3D.cm35.(2015·福建,9)某几何体的三视图如图所示,则该几何体的表面积等于()A.8+2B.11+2C.14+2D.156.(2014·辽宁,7)某几何体三视图如图所示,则该几何体的体积为()A.8-B.8-C.8-πD.8-2π7.(2014·浙江,3)某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.72cm3B.90cm3C.108cm3D.138cm38.(2014·新课标全国Ⅰ,8)如图,网格纸的各小格都是正方形,粗实线画出的是一个几何体的三视图,则这个几何体是()A.三棱锥B.三棱柱C.四棱锥D.四棱柱9.(2014·新课标全国Ⅱ,6)如图,网格纸上正方形小格的边长为1(表示1cm),图中粗线画出的是某零件的三视图,该零件由一个底面半径为3cm,高为6cm的圆柱体毛坯切削得到,则切削掉部分的体积与原来毛坯体积的比值为()A.B.C.D.10.(2015·天津,10)一个几何体的三视图如图所示(单位:m),则该几何体的体积为________m3.11.(2014·北京,11)某三棱锥的三视图如图所示,则该三棱锥最长棱的棱长为________.B组两年模拟精选(2016~2015年)1.(2016·成都市一诊)若一个几何体的正视图和侧视图是两个全等的正方形,则这个几何体的俯视图不可能是()2.(2016·湖南衡阳大联考)如图是一个几何体的三视图,在该几何体的各个面中,面积最小的面的面积为()A.4B.4C.4D.83.(2016·桂林市一调)已知底面为正方形的四棱锥,其一条侧棱垂直于底面,那么该四棱锥的三视图可能是下列各图中的()4.(2016·石家庄二中一模)如图是一个几何体的三视图,则该几何体任意两个顶点间距离的最大值为()A.4B.5C.3D.35.(2015·北京朝阳区期末)一个四棱锥的三视图如图所示,则该四棱锥的侧面中,直角三角形的个数为()A.1B.2C.3D.46.(2015·山西质量监测)某几何体的正视图与俯视图如图所示,若俯视图中的多边形为正六边形,则该几何体的侧视图的面积为()A.B.6+C.+3D.47.(2015·江西师大附中、宜春中学联考)某几何体的直观图如图所示,该几何体的正视图和侧视图可能正确的是()8.(2015·辽宁沈阳质量监测)如图,网格纸上小正方形的边长为1,粗线画出的是某多面体的三视图,则该几何体的各个面中最大面的面积为()A.1B.C.D.2答案精析A组三年高考真题(2016~2014年)1.解析四棱锥的直观图如图所示,PC⊥平面ABCD,PC=1,底面四边形ABCD为正方形且边长为1,最长棱长PA==.答案C2.解析该几何体由一个圆柱和一个从轴截面截开的“半圆锥”组成,其体积为V=π×12×2+×π×12×1=2π+=.答案B3.解析由三视图可知原几何体为半圆柱,底面半径为1,高为2,则表面积为:S=2×π×12+×2π×1×2+2×2=π+2π+4=4+3π.答案D4.解析由三视图可知该几何体是由棱长为2cm的正方体与底面为边长为2cm正方形、高为2cm的四棱锥组成,V=V正方体+V四棱锥=8cm3+cm3=cm3.故选C.答案C5.解析该几何体为底面是直角梯形的直四棱柱.S表=2×(1+2)×1+2×1+2×1+2×2+2×=11+2,故选B.答案B6.解析该几何体是一个正方体截去两个四分之一圆柱形成的组合体,其体积V=23-×π×12×2×2=8-π,故选C.答案C7.解析由三视图可知,该几何体的直观图如图所示,则该几何体的体积V=V四棱柱+V三棱柱=4×6×3+×4×3×3=90(cm3).答案B8.解析由题知,该几何体的三视图为一个三角形,两个四边形,分析可知该几何体为三棱柱,答案B9.解析由三视图可知该零件是一个底面半径为2、高为4的圆柱和一个底面半径为3、高为2的圆柱的组合体,所以该组合体的体积V1=π·22·4+π·32·2=34π,原来的圆柱体毛坯的体积为V=π·32·6=54π,则切削掉部分的体积为V2=54π-34π=20π,所以切削掉部分的体积与原来的圆柱体毛坯体积的比值为=.故选C.答案C10...