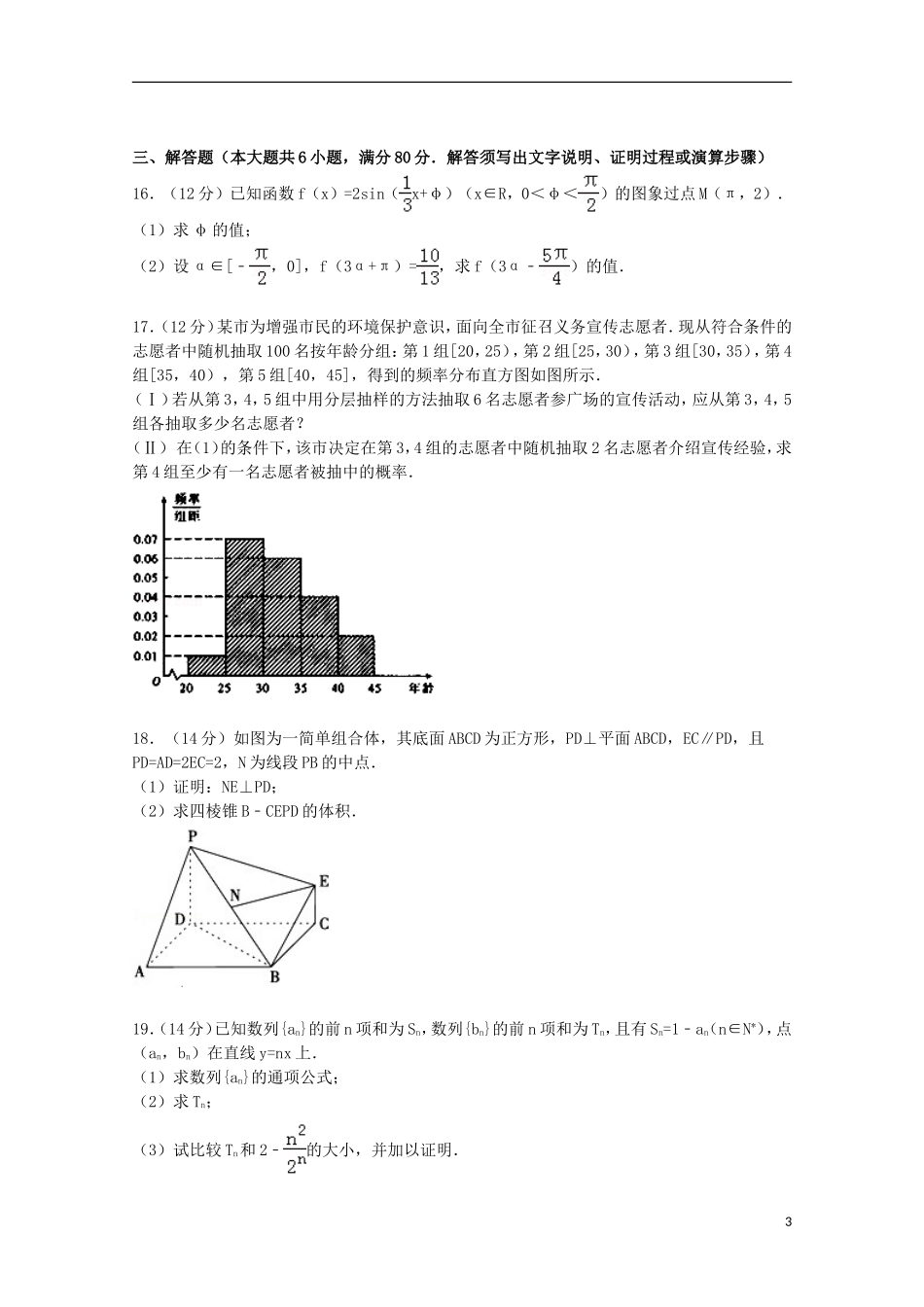
广东省茂名市2015届高考数学二模试卷(文科)一、选择题:(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1.(5分)已知集合A={1,2},B={﹣2,1,2},则A∩B等于()A.{﹣2}B.{1}C.{1,2}D.{﹣1,1,2}2.(5分)复数1﹣(i为虚数单位)在复平面上对应的点的坐标是()A.(1,1)B.(1,﹣1)C.(﹣1,1)D.(﹣1,﹣1)3.(5分)等差数列{an}的前n项和为Sn,已知a3=3,S3=6,则a10的值是()A.1B.3C.10D.554.(5分)已知向量=(2,1),=(x,﹣2),若∥,则+等于()A.(﹣2,﹣1)B.(2,1)C.(3,﹣1)D.(﹣3,1)5.(5分)若x,y满足不等式,则2x+y的最小值为()A.0B.﹣4C.4D.36.(5分)命题“∃x0∈R,x02+2x0+2≤0”的否定是()A.∀x∈R,x2+2x+2>0B.∀x∈R,x2+2x+2≥0C.∃x0∈R,x02+2x0+2<0D.∃x∈R,x02+2x0+2>07.(5分)已知平面α⊥平面β,α∩β=l,点A∈α,A∉l,作直线AC⊥l,现给出下列四个判断:(1)AC与l相交,(2)AC⊥α,(3)AC⊥β,(4)AC∥β.则可能成立的个数为()A.1B.2C.3D.48.(5分)如图所示,程序框图的输出结果是s=,那么判断框中应填入的关于n的判断条件是()1A.n≤8?B.n<8?C.n≤10?D.n<10?9.(5分)已知抛物线y2=4x与双曲线﹣=1(a>0,b>0)有相同的焦点F,点A,B是两曲线的交点,O为坐标原点,若(+)•=0,则双曲线的实轴长为()A.+2B.﹣1C.2﹣1D.2﹣210.(5分)已知函数f(x)的定义域为(0,+∞),若y=在(0,+∞)上为增函数,则称f(x)为“一阶比增函数”;若y=在(0,+∞)上为增函数,则称f(x)为“二阶比增函数”.我们把所有“一阶比增函数”组成的集合记为Ω1,所有“二阶比增函数”组成的集合记为Ω2.若函数f(x)=x3﹣2hx2﹣hx,且f(x)∈Ω1,f(x)∉Ω2,则实数h的取值范围是()A.[0,+∞)B.(0,+∞)C.(﹣∞,0]D.(﹣∞,0)二、填空题:(本大题共3小题,考生作答4小题,每小题5分,满分15分)(一)必做题(11~13题)11.(5分)函数f(x)=的定义域为.12.(5分)函数y=2lnx+1在点(1,1)处的切线方程为.13.(5分)在△ABC中,角A,B,C所对的边分别为a,b,c,已知a(sinA﹣sinB)=csinC﹣bsinB,且2a=c,则sinA=.一、(二)选做题(14~15题,考生只能从中选做一题,两题都答的,只计算第一题的得分.)坐标系与参数方程选做题14.(5分)在平面直角坐标系中,圆C的参数方程为(θ为参数),则坐标原点到该圆的圆心的距离为.一、几何证明选讲选做题15.如图,CD是圆O的切线,切点为C,BC=2,点B在圆上,∠BCD=60°,则圆的面积为.2三、解答题(本大题共6小题,满分80分.解答须写出文字说明、证明过程或演算步骤)16.(12分)已知函数f(x)=2sin(x+φ)(x∈R,0<φ<)的图象过点M(π,2).(1)求φ的值;(2)设α∈[﹣,0],f(3α+π)=,求f(3α﹣)的值.17.(12分)某市为增强市民的环境保护意识,面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄分组:第1组[20,25),第2组[25,30),第3组[30,35),第4组[35,40),第5组[40,45],得到的频率分布直方图如图所示.(Ⅰ)若从第3,4,5组中用分层抽样的方法抽取6名志愿者参广场的宣传活动,应从第3,4,5组各抽取多少名志愿者?(Ⅱ)在(1)的条件下,该市决定在第3,4组的志愿者中随机抽取2名志愿者介绍宣传经验,求第4组至少有一名志愿者被抽中的概率.18.(14分)如图为一简单组合体,其底面ABCD为正方形,PD⊥平面ABCD,EC∥PD,且PD=AD=2EC=2,N为线段PB的中点.(1)证明:NE⊥PD;(2)求四棱锥B﹣CEPD的体积.19.(14分)已知数列{an}的前n项和为Sn,数列{bn}的前n项和为Tn,且有Sn=1﹣an(n∈N*),点(an,bn)在直线y=nx上.(1)求数列{an}的通项公式;(2)求Tn;(3)试比较Tn和2﹣的大小,并加以证明.320.(14分)已知中心在原点,焦点在坐标轴上的椭圆E:+=1(a>b>0)过点P(,),离心率为,(1)求椭圆E的方程;(2)设直线l过椭圆E的右焦点F,且交椭...