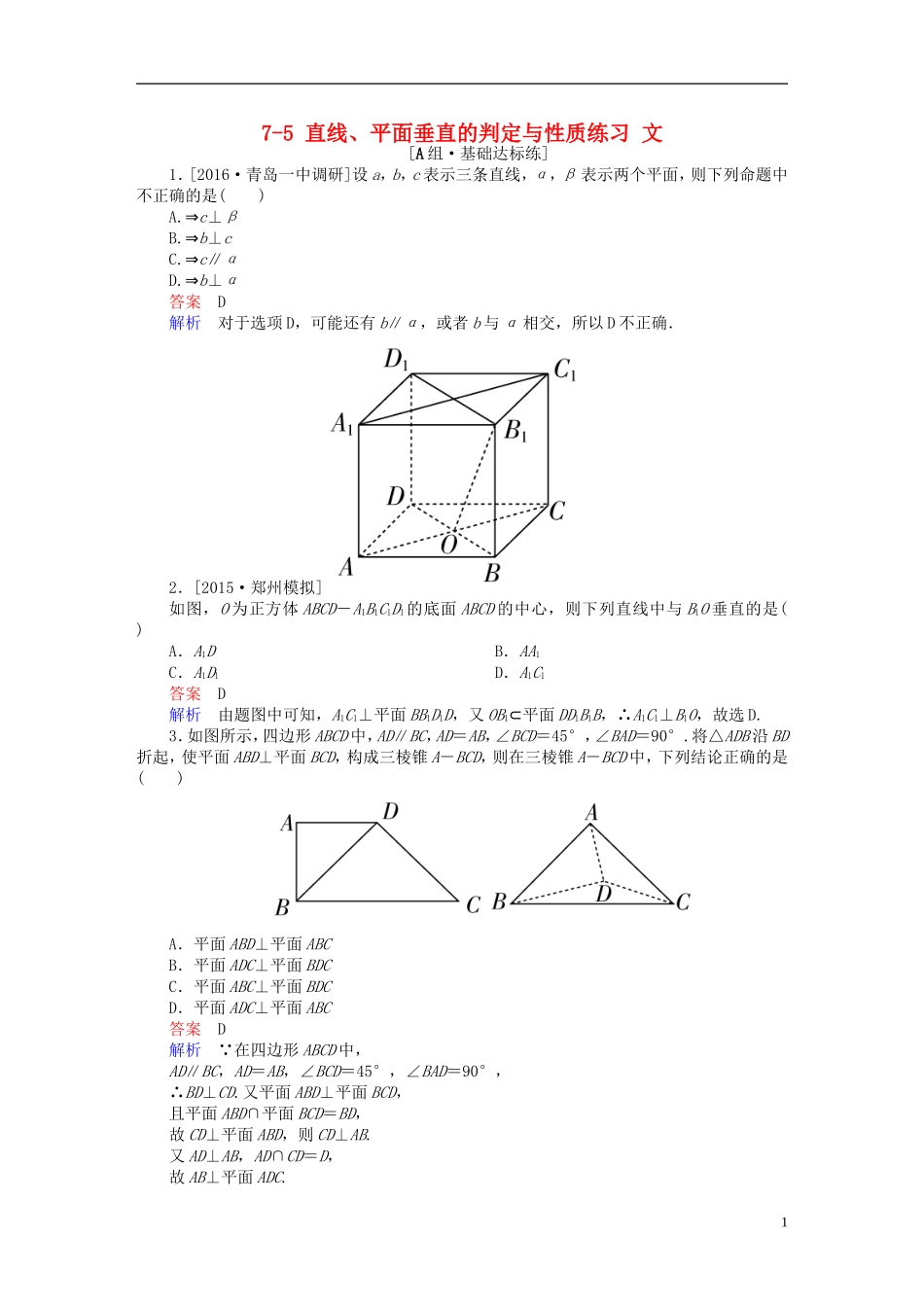
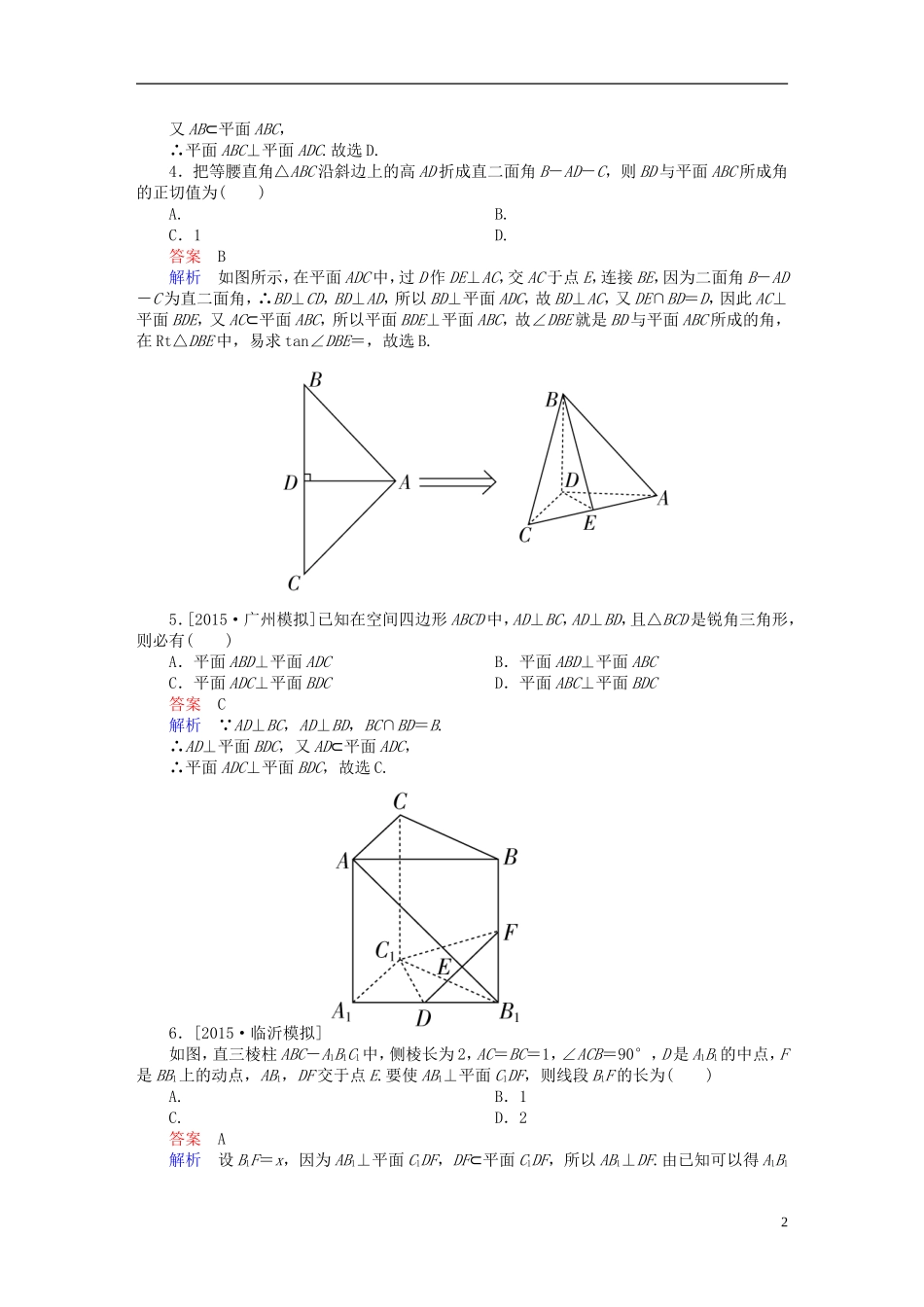
7-5直线、平面垂直的判定与性质练习文[A组·基础达标练]1.[2016·青岛一中调研]设a,b,c表示三条直线,α,β表示两个平面,则下列命题中不正确的是()A.⇒c⊥βB.⇒b⊥cC.⇒c∥αD.⇒b⊥α答案D解析对于选项D,可能还有b∥α,或者b与α相交,所以D不正确.2.[2015·郑州模拟]如图,O为正方体ABCD-A1B1C1D1的底面ABCD的中心,则下列直线中与B1O垂直的是()A.A1DB.AA1C.A1D1D.A1C1答案D解析由题图中可知,A1C1⊥平面BB1D1D,又OB1⊂平面DD1B1B,∴A1C1⊥B1O,故选D.3.如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是()A.平面ABD⊥平面ABCB.平面ADC⊥平面BDCC.平面ABC⊥平面BDCD.平面ADC⊥平面ABC答案D解析 在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,∴BD⊥CD.又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD,故CD⊥平面ABD,则CD⊥AB.又AD⊥AB,AD∩CD=D,故AB⊥平面ADC.1又AB⊂平面ABC,∴平面ABC⊥平面ADC.故选D.4.把等腰直角△ABC沿斜边上的高AD折成直二面角B-AD-C,则BD与平面ABC所成角的正切值为()A.B.C.1D.答案B解析如图所示,在平面ADC中,过D作DE⊥AC,交AC于点E,连接BE,因为二面角B-AD-C为直二面角,∴BD⊥CD,BD⊥AD,所以BD⊥平面ADC,故BD⊥AC,又DE∩BD=D,因此AC⊥平面BDE,又AC⊂平面ABC,所以平面BDE⊥平面ABC,故∠DBE就是BD与平面ABC所成的角,在Rt△DBE中,易求tan∠DBE=,故选B.5.[2015·广州模拟]已知在空间四边形ABCD中,AD⊥BC,AD⊥BD,且△BCD是锐角三角形,则必有()A.平面ABD⊥平面ADCB.平面ABD⊥平面ABCC.平面ADC⊥平面BDCD.平面ABC⊥平面BDC答案C解析 AD⊥BC,AD⊥BD,BC∩BD=B.∴AD⊥平面BDC,又AD⊂平面ADC,∴平面ADC⊥平面BDC,故选C.6.[2015·临沂模拟]如图,直三棱柱ABC-A1B1C1中,侧棱长为2,AC=BC=1,∠ACB=90°,D是A1B1的中点,F是BB1上的动点,AB1,DF交于点E.要使AB1⊥平面C1DF,则线段B1F的长为()A.B.1C.D.2答案A解析设B1F=x,因为AB1⊥平面C1DF,DF⊂平面C1DF,所以AB1⊥DF.由已知可以得A1B12=,矩形ABB1A1中,tan∠FDB1=,tan∠A1AB1==,又∠FDB1=∠A1AB1,所以=,故B1F=×=.故选A.7.[2016·大连模拟]已知a、b、l表示三条不同的直线,α、β、γ表示三个不同的平面,有下列四个命题:①若α∩β=a,β∩γ=b,且a∥b,则α∥γ;②若a、b相交,且都在α、β外,a∥α,a∥β,b∥α,b∥β,则α∥β;③若α⊥β,α∩β=a,b⊂β,a⊥b,则b⊥α;④若a⊂α,b⊂α,l⊥a,l⊥b,l⊄α,则l⊥α.其中正确命题的序号是________.答案②③解析若平面α、β、γ两两相交于三条直线,则有交线平行,故①不正确.因为a、b相交,假设其确定的平面为γ,根据a∥α,b∥α,可得γ∥α.同理可得γ∥β,因此α∥β,②正确.由面面垂直的性质定理知③正确.当a∥b时,l垂直于平面α内两条不相交直线,不能得出l⊥α,④错误.8.[2016·潍坊质检]如图所示,在四棱锥P-ABCD中,PA⊥底面ABCD,且底面各边都相等,M是PC上的一动点,当点M满足________时,平面MBD⊥平面PCD.(只要填写一个你认为是正确的条件即可)答案DM⊥PC(或BM⊥PC)解析连接AC,BD交于O, 底面各边相等,∴BD⊥AC;又PA⊥底面ABCD,∴PA⊥BD,又PA∩AC=A,∴BD⊥平面PAC,∴BD⊥PC.∴当DM⊥PC(或BM⊥PC)时,即有PC⊥平面MBD.而PC⊂平面PCD,∴平面MBD⊥平面PCD.9.四棱锥P-ABCD中,底面ABCD是正方形,顶点在底面上的射影是底面正方形的中心,一个对角面的面积是一个侧面面积的倍,则侧面与底面所成锐二面角等于______.答案3解析如图所示,根据=,得=,即为侧面与底面所成锐二面角的正弦值,故侧面与底面所成锐二面角为.10.如图,在四棱锥P-ABCD中,AB∥CD,AB⊥AD,CD=2AB,平面PAD⊥底面ABCD,PA⊥AD,E和F分别是CD,PC的中点.求证:(1)PA⊥底面ABCD;(2)BE∥平面PAD;(3)平面BEF⊥平面PCD.证明(1) 平面PAD∩平面ABCD=AD,平面PAD⊥平面ABCD,且PA⊥AD,∴PA⊥底面ABCD.(2)...