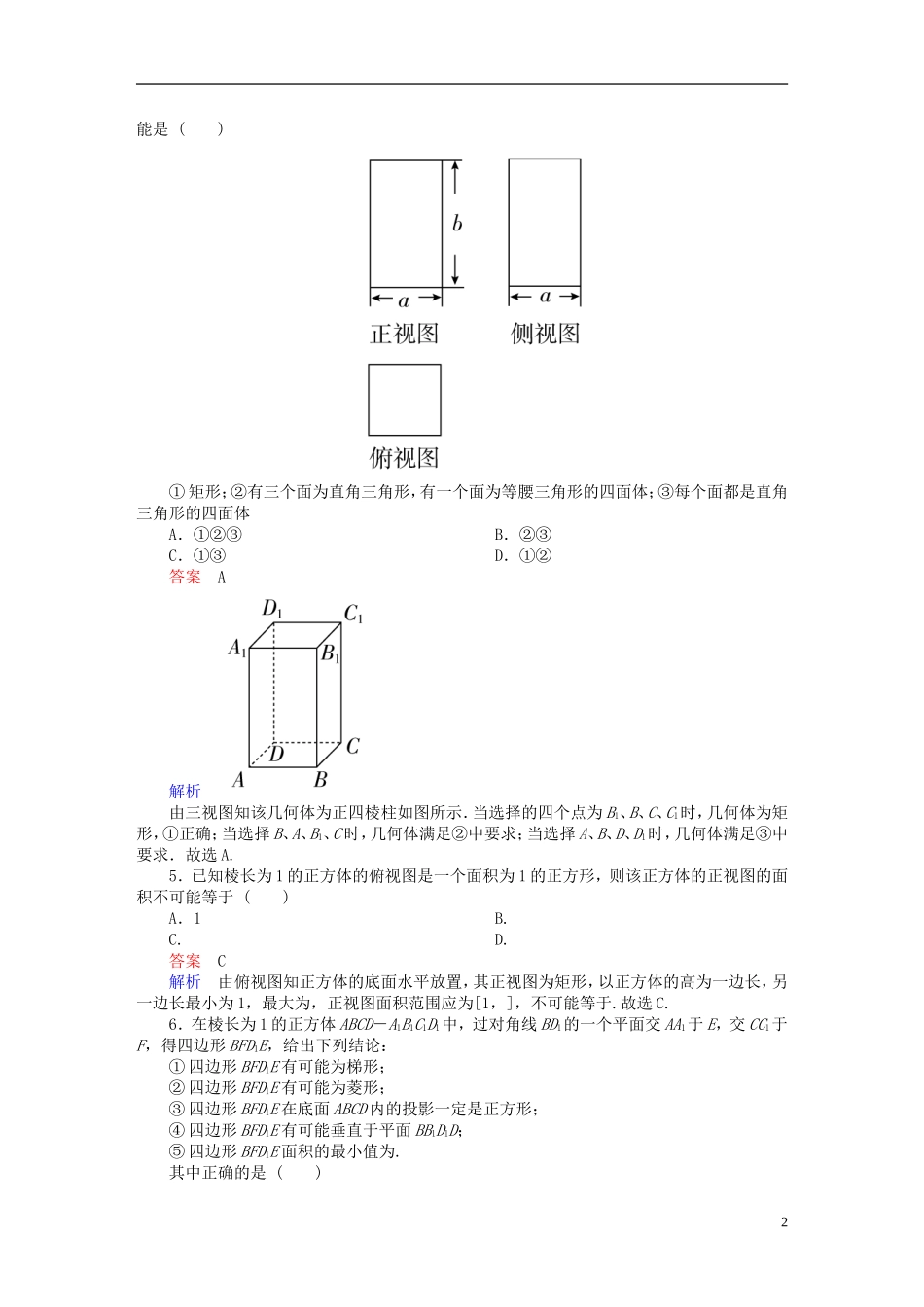
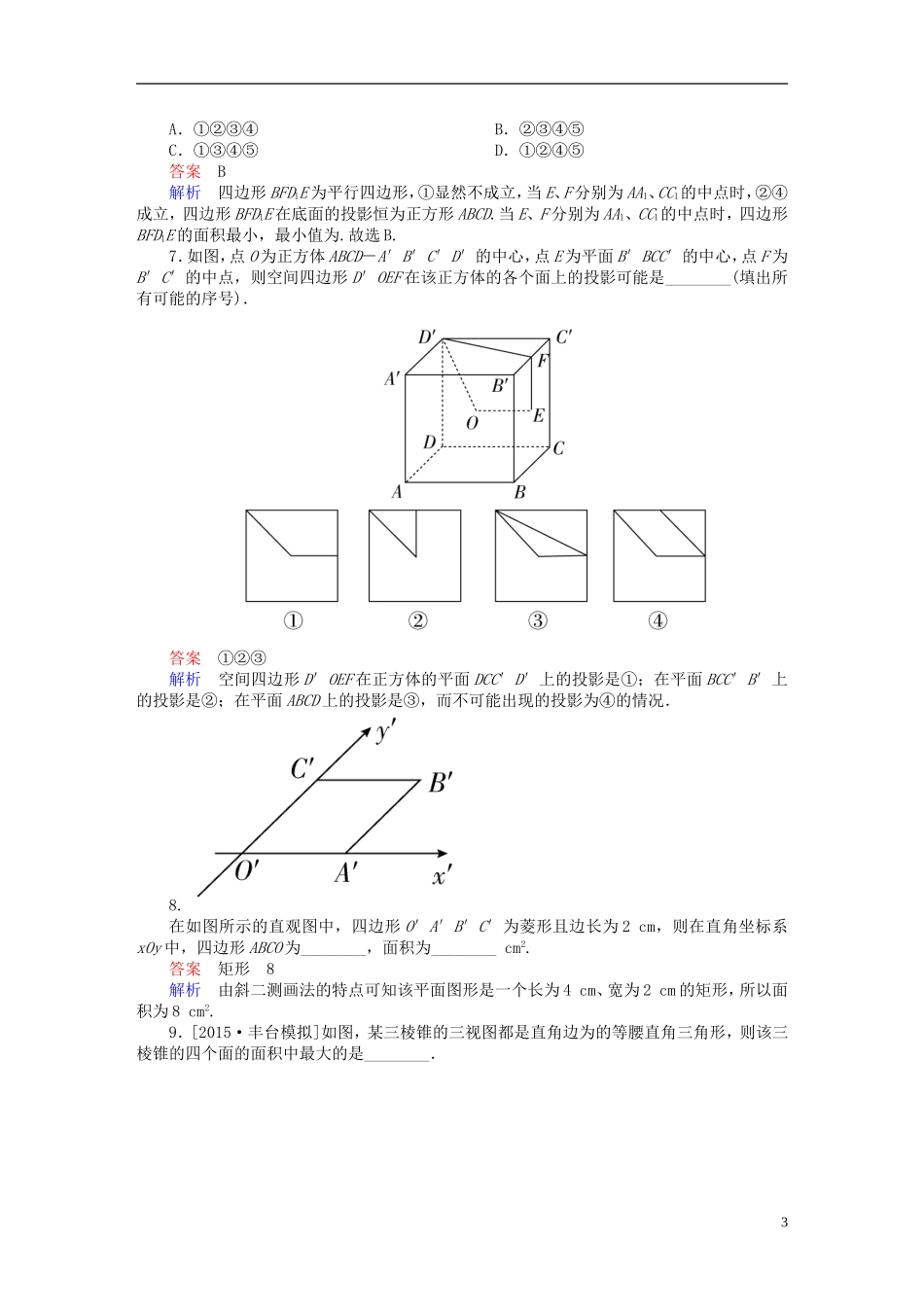
第七章立体几何7.1空间几何体的结构及其三视图和直观图练习理[A组·基础达标练]1.[2016·潍坊模拟]一个几何体的三视图形状都相同、大小均相等,那么这个几何体不可以是()A.球B.三棱锥C.正方体D.圆柱答案D解析球、正方体的三视图形状都相同,大小均相等.三棱锥的三条侧棱相等且两两垂直时,其三视图的形状都相同,大小均相等.不论圆柱如何放置,其三视图的形状都不会完全相同,故选D.2.下列命题中正确的是()A.有两个面平行,其余各面都是四边形的几何体叫棱柱B.有两个面平行,其余各面都是平行四边形的几何体叫棱柱C.有一个面是多边形,其余各面都是三角形的几何体叫棱锥D.棱台各侧棱的延长线交于一点答案D解析棱柱的结构特征有三个方面:有两个面互相平行;其余各面是平行四边形;这些平行四边形所在面中,每相邻两个面的公共边都互相平行.由此可知选项A、B均不正确;各面都是三角形的几何体并不一定是棱锥,如正八面体,故选项C不正确.棱台是由棱锥被平行于棱锥底面的平面截去一部分得到的,故可知棱台各侧棱的延长线交于一点,故选D.3.[2015·海口模拟]如图是一个物体的三视图,则此三视图所描述物体的直观图是()答案D解析由俯视图可排除A、C,由正视图和侧视图可知B错,故选D.4.[2016·云南师大附中月考]已知一几何体的三视图如图所示,正视图和侧视图都是矩形,俯视图为正方形,在该几何体上任意选择4个顶点,以这4个点为顶点的几何体(图形)可1能是()①矩形;②有三个面为直角三角形,有一个面为等腰三角形的四面体;③每个面都是直角三角形的四面体A.①②③B.②③C.①③D.①②答案A解析由三视图知该几何体为正四棱柱如图所示.当选择的四个点为B1、B、C、C1时,几何体为矩形,①正确;当选择B、A、B1、C时,几何体满足②中要求;当选择A、B、D、D1时,几何体满足③中要求.故选A.5.已知棱长为1的正方体的俯视图是一个面积为1的正方形,则该正方体的正视图的面积不可能等于()A.1B.C.D.答案C解析由俯视图知正方体的底面水平放置,其正视图为矩形,以正方体的高为一边长,另一边长最小为1,最大为,正视图面积范围应为[1,],不可能等于.故选C.6.在棱长为1的正方体ABCD-A1B1C1D1中,过对角线BD1的一个平面交AA1于E,交CC1于F,得四边形BFD1E,给出下列结论:①四边形BFD1E有可能为梯形;②四边形BFD1E有可能为菱形;③四边形BFD1E在底面ABCD内的投影一定是正方形;④四边形BFD1E有可能垂直于平面BB1D1D;⑤四边形BFD1E面积的最小值为.其中正确的是()2A.①②③④B.②③④⑤C.①③④⑤D.①②④⑤答案B解析四边形BFD1E为平行四边形,①显然不成立,当E、F分别为AA1、CC1的中点时,②④成立,四边形BFD1E在底面的投影恒为正方形ABCD.当E、F分别为AA1、CC1的中点时,四边形BFD1E的面积最小,最小值为.故选B.7.如图,点O为正方体ABCD-A′B′C′D′的中心,点E为平面B′BCC′的中心,点F为B′C′的中点,则空间四边形D′OEF在该正方体的各个面上的投影可能是________(填出所有可能的序号).答案①②③解析空间四边形D′OEF在正方体的平面DCC′D′上的投影是①;在平面BCC′B′上的投影是②;在平面ABCD上的投影是③,而不可能出现的投影为④的情况.8.在如图所示的直观图中,四边形O′A′B′C′为菱形且边长为2cm,则在直角坐标系xOy中,四边形ABCO为________,面积为________cm2.答案矩形8解析由斜二测画法的特点可知该平面图形是一个长为4cm、宽为2cm的矩形,所以面积为8cm2.9.[2015·丰台模拟]如图,某三棱锥的三视图都是直角边为的等腰直角三角形,则该三棱锥的四个面的面积中最大的是________.3答案解析由三视图可知,该几何体的直观图如图所示.AB,AC,AD两两垂直,且均为,所以四个面中面积最大的为△BCD,且△BCD是边长为2的正三角形,所以S△BCD=×2×2×=.10.[2015·朝阳模拟]已知三棱锥的底面是边长为1的正三角形,其正视图与俯视图如图所示,则其侧视图的面积为________.4答案解析由正视图与俯视图可知,该几何体侧视图的面积为××=.[B组·能力提升练]1.[2016·长春质检]某几何体的三视图如图所示,则它的表面积为()A.2+πB.2+...