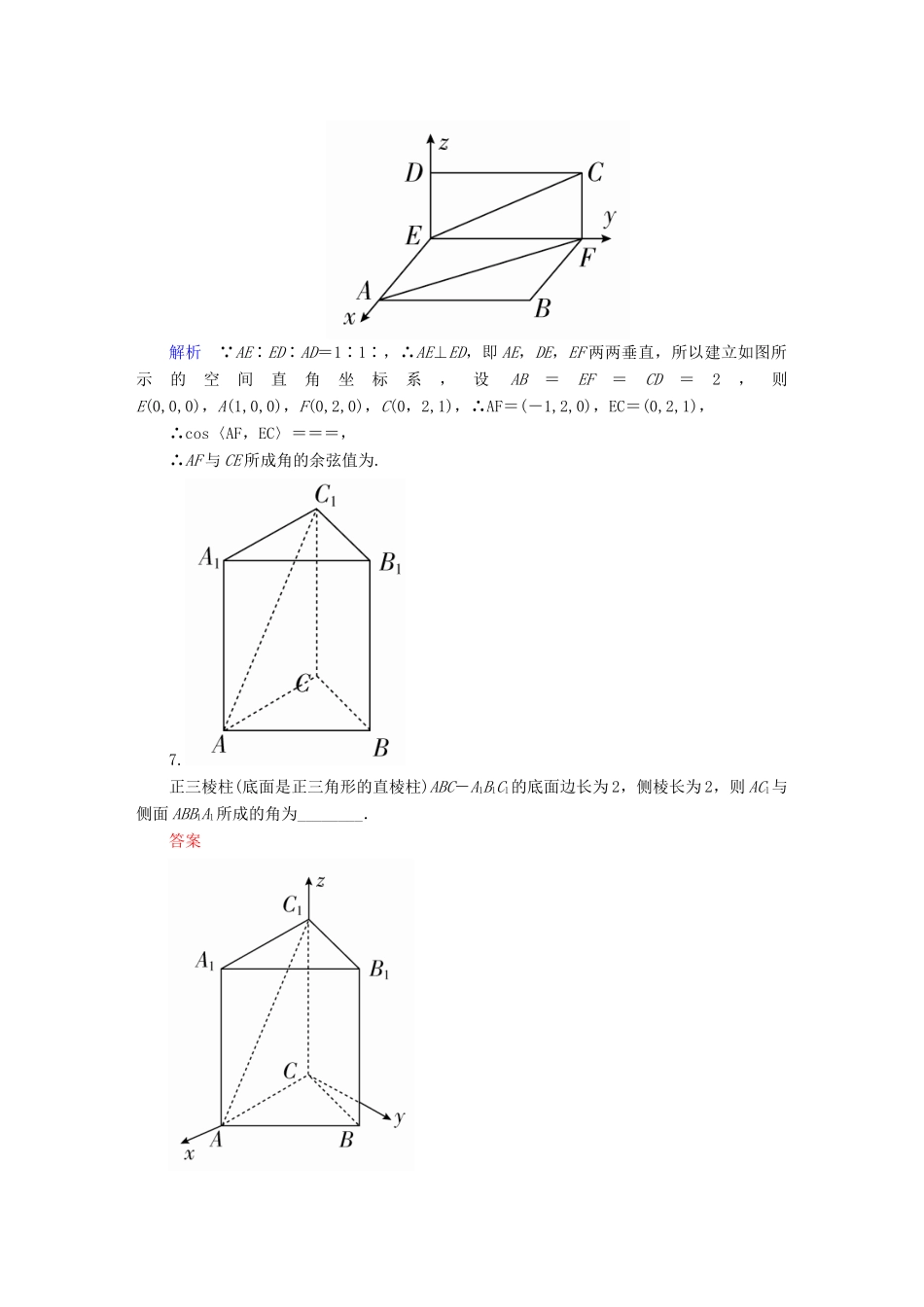
2018版高考数学一轮总复习第7章立体几何7.7立体几何中的向量方法模拟演练理[A级基础达标](时间:40分钟)1.若平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,-1,0),则平面α和平面β的位置关系是()A.平行B.相交但不垂直C.垂直D.重合答案C解析由(1,2,0)·(2,-1,0)=1×2+2×(-1)+0×0=0,知两平面的法向量互相垂直,所以两平面互相垂直.2.[2017·宜宾模拟]已知向量a=(1,1,0),b=(-1,0,2),且ka+b与2a-b互相平行,则k的值是()A.-2B.C.D.答案A解析由题意得,ka+b=(k-1,k,2),2a-b=(3,2,-2).所以==,解得k=-2.3.[2017·金华模拟]在空间直角坐标系Oxyz中,平面OAB的一个法向量为n=(2,-2,1),已知点P(-1,3,2),则点P到平面OAB的距离d等于()A.4B.2C.3D.1答案B解析由已知平面OAB的一条斜线的方向向量OP=(-1,3,2),所以点P到平面OAB的距离d=|OP|·|cos〈OP,n〉|===2.4.在三棱锥P-ABC中,PA⊥平面ABC,∠BAC=90°,D,E,F分别是棱AB,BC,CP的中点,AB=AC=1,PA=2,则直线PA与平面DEF所成角的正弦值为()A.B.C.D.答案C解析以A为原点,AB,AC,AP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,由AB=AC=1,PA=2,得A(0,0,0),B(1,0,0),C(0,1,0),P(0,0,2),D,0,0,E,,0,F,∴PA=(0,0,-2),DE=,DF=.设平面DEF的法向量为n=(x,y,z),则由得取z=1,则n=(2,0,1),设PA与平面DEF所成的角为θ,则sinθ==,∴PA与平面DEF所成角的正弦值为.5.已知直三棱柱ABC-A1B1C1中,∠ACB=90°,AC=1,CB=,侧棱AA1=1,侧面AA1B1B的两条对角线交于点D,则平面B1BD与平面CBD所成的二面角的余弦值为()A.-B.-C.D.答案A解析建立如图所示的空间直角坐标系,则C(0,0,0),B(,0,0),A(0,1,0),B1(,0,1),D,CD=,CB=(,0,0),BA=(-,1,0),BB1=(0,0,1).设平面CBD和平面B1BD的法向量分别为n1,n2,可得n1=(0,1,-1),n2=(1,,0),所以cos〈n1,n2〉==,又平面B1BD与平面CBD所成的二面角的平面角与〈n1,n2〉互补,故平面B1BD与平面CBD所成的二面角的余弦值为-.6.如图,在正方形ABCD中,EF∥AB,若沿EF将正方形折成一个二面角后,AE∶ED∶AD=1∶1∶,则AF与CE所成角的余弦值为________.答案解析 AE∶ED∶AD=1∶1∶,∴AE⊥ED,即AE,DE,EF两两垂直,所以建立如图所示的空间直角坐标系,设AB=EF=CD=2,则E(0,0,0),A(1,0,0),F(0,2,0),C(0,2,1),∴AF=(-1,2,0),EC=(0,2,1),∴cos〈AF,EC〉===,∴AF与CE所成角的余弦值为.7.正三棱柱(底面是正三角形的直棱柱)ABC-A1B1C1的底面边长为2,侧棱长为2,则AC1与侧面ABB1A1所成的角为________.答案解析以C为原点建立坐标系,得下列坐标:A(2,0,0),C1(0,0,2).点C1在侧面ABB1A1内的射影为点C2.所以AC1=(-2,0,2),AC2=,,2,设直线AC1与平面ABB1A1所成的角为θ,则cosθ===.又θ∈,所以θ=.8.已知点E,F分别在正方体ABCD-A1B1C1D1的棱BB1,CC1上,且B1E=2EB,CF=2FC1,则面AEF与面ABC所成的锐二面角的正切值为________.答案解析如图,建立空间直角坐标系Dxyz,设DA=1,由已知条件得A(1,0,0),E,F,AE=,AF=,设平面AEF的法向量为n=(x,y,z),面AEF与面ABC所成的锐二面角为θ,由图知θ为锐角,由得令y=1,z=-3,x=-1,则n=(-1,1,-3),平面ABC的法向量为m=(0,0,-1),cosθ=|cos〈n,m〉|=,tanθ=.9.如图,在直二面角E-AB-C中,四边形ABEF是矩形,AB=2,AF=2,△ABC是以A为直角顶点的等腰直角三角形,点P是线段BF上的一点,PF=3.(1)证明:FB⊥平面PAC;(2)求异面直线PC与AB所成的角的余弦值.解(1)证明:以A为原点,向量AB,AC,AF的方向分别为x,y,z轴的正方向建立空间直角坐标系,则A(0,0,0),B(2,0,0),C(0,2,0),F(0,0,2). BF==4,PF=3,∴P,FB=(2,0,-2),AC=(0,2,0),AP=. FB·AC=0,∴FB⊥AC. FB·AP=0,∴FB⊥AP. FB⊥AC,FB⊥AP,AC∩AP=A,∴FB⊥平面APC.(2) AB=(2,0,0),PC=,记AB与PC夹角为θ,则|cosθ|===.10.如图,在直棱柱ABCD-A1B1C1D1中,AD...