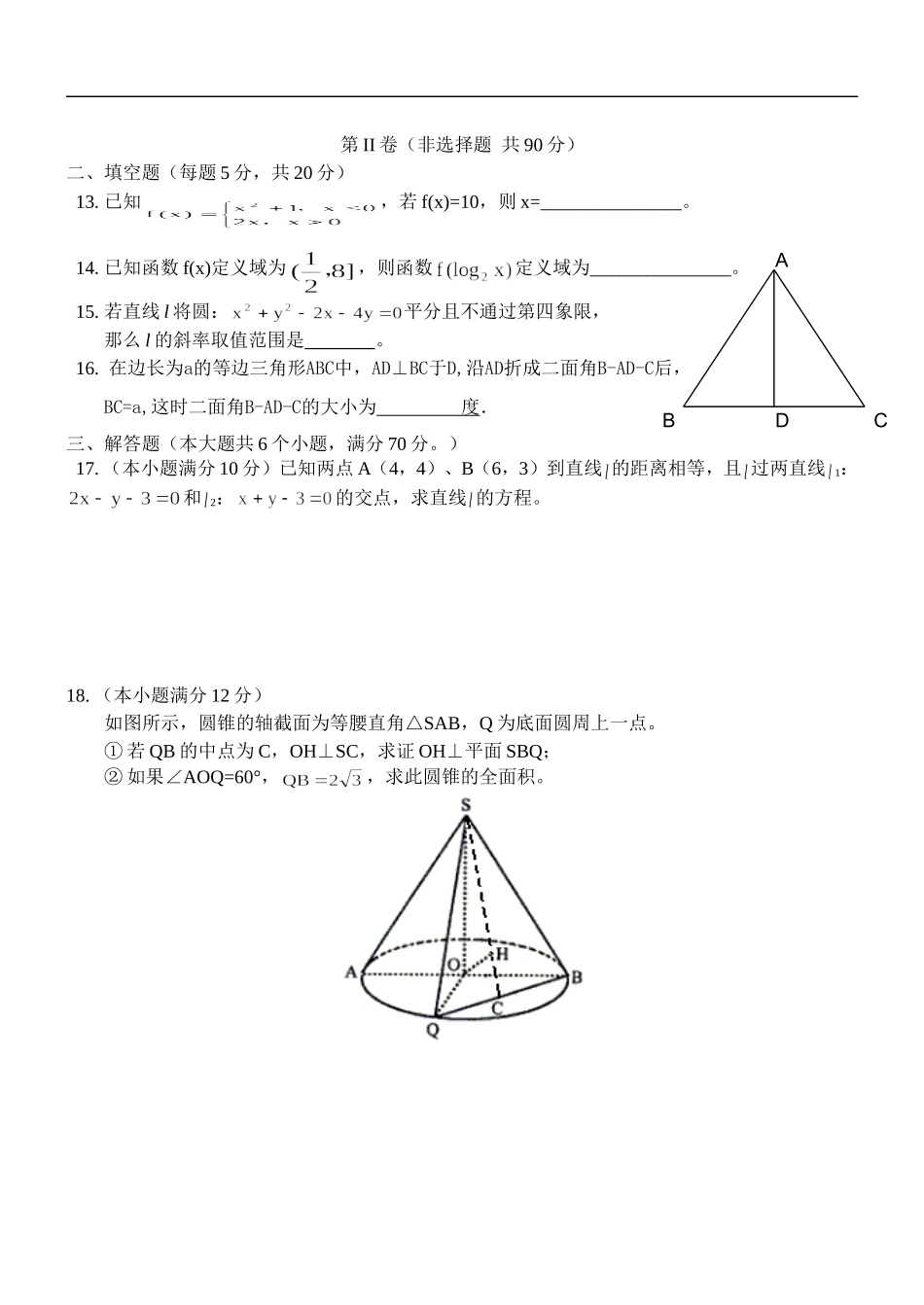
汤阴一中2008—2009学年上学期高一期末考试数学试卷(时间:120分钟,总分:150)命题人:姜健刚一、选择题(本大题共12小题,每小题5分,共计60分。)1.若集合()A.B.C.D.2.函数()A.是偶函数,在区间()上单调递增B.是偶函数,在区间(,0)上单调递减C.是奇函数,在区间(0,+)上单调递增D.是奇函数,在区间(0,+)上单凋递减3.函数的图象是()A.B.C.D.4.记函数的反函数,则g(10)等于()A.2B.-2C.3D.-15.如图,将无盖正方体纸盒展开,直线AB、CD在原正方体中的位置关系是()A.平行B.相交且垂直C.不相交也不平行D.相交成60°6.设m、n是两条不重合的直线,α、β、是三个不重合的平面,给出下列四个命题:①若m⊥α,n//α,则m⊥n②若α//β,β//,m⊥α,则m⊥③若m//α,n//α,则m//n④若α⊥,,则α//β其中正确命题的序号是()A.①和②B.②和③C.③和④D.①和④7.直线与圆交于E、F两点,则EOF(O为原点)的面积为()A、B、C、D、8.到定点(1,0,0)的距离小于或等于1的点的集合是()A.B.C.D.9.等体积的球与等边圆柱(轴截面是正方形的圆柱)的表面积为,则等于()A.B.C.D.10.直线垂直,则a的值是()A.-1或B.1或C.D.11.与圆相切,且在x轴、y轴上的截距相等的直线共有()A.4条B.3条C.2条D.1条12.如图,在直角坐标系的第一象限内,△AOB是边长为2的等边三角形,设直线l:x=t()截这个三角形,所得位于直线左侧的图形的面积为f(t),则函数y=f(t)的图象只可能是()A.B.C.D.第II卷(非选择题共90分)二、填空题(每题5分,共20分)13.已知,若f(x)=10,则x=_______________。14.已知函数f(x)定义域为,则函数定义域为_______________。15.若直线l将圆:平分且不通过第四象限,那么l的斜率取值范围是。16.在边长为a的等边三角形ABC中,AD⊥BC于D,沿AD折成二面角B-AD-C后,BC=a,这时二面角B-AD-C的大小为度.三、解答题(本大题共6个小题,满分70分。)17.(本小题满分10分)已知两点A(4,4)、B(6,3)到直线的距离相等,且过两直线1:和2:的交点,求直线的方程。18.(本小题满分12分)如图所示,圆锥的轴截面为等腰直角△SAB,Q为底面圆周上一点。①若QB的中点为C,OH⊥SC,求证OH⊥平面SBQ;②如果∠AOQ=60°,,求此圆锥的全面积。DABC19.(本小题满分12分)已知:正四棱锥S—ABCD的棱长均为13,E、F分别是SA、BD上的点,且SE:EA=BF:FD=5:8。①求证:直线EF//平面SBC;②求四棱锥S—ABCD的体积。20.(本小题满分12分)我国加入WTO时,根据达成的协议,若干年内某产品关税和市场供应量P的关系允许近似满足,其中t为关税的税率,且,x为市场价格,b、k为正常数,当时,市场供应量如图所示。①根据图象求b、k的值;②记市场需求量为Q,它近似满足,当P=Q时的市场价格为市场平衡价格,为使市场平衡价格不低于9元,求税率的最大值。21.(本小题满分12分)设,定义在区间(-b,b)内的函数是奇函数。①求b的取值范围;②判断并用定义证明函数f(x)的单调性。22.(本小题满分12分)已知圆C:,问是否存在斜率为1的直线,使以被圆C截得的弦AB为直径的圆经过原点。若存在,写出直线的方程;若不存在,说明理由。[参考答案]一、选择题1.C2.B3.B4.B5.D6.A7.D8.A9.D10.D11.C12.C二、填空题13.-3或514.15.[0,2]16.60三、计算题17.解:由方程组得………………………………2分故l的方程为:,由题意知解得………………………………8分所以l的方程为:……………………10分18.解:(1)证明:连结OC SQ=SBOQ=OBQC=CB∴QB⊥SC,QB⊥OC……………………………………2分∴QB⊥平面SOC OH平面SOC∴QB⊥OH………………………………………………4分又 OH⊥SC∴OH⊥平面SQB…………………………………………6分(2)解:连结AQ Q为底面圆周的一点,AB为直径∴AQ⊥QB…………………………………………8分在Rt△AQB中,∠QBA=30°,∴ △SAB是等腰直角三角形∴SA=……………………………………………………10分∴……………………12分19.①证明:在SD上取一点P,使SP:PD=5:8连EP,则EP//AD又AD//BC∴EP//BC……………………………………2分连FP,且SP:PD=BF:FD...