高考数学复习点拨 函数模型及其应用教材解读VIP免费

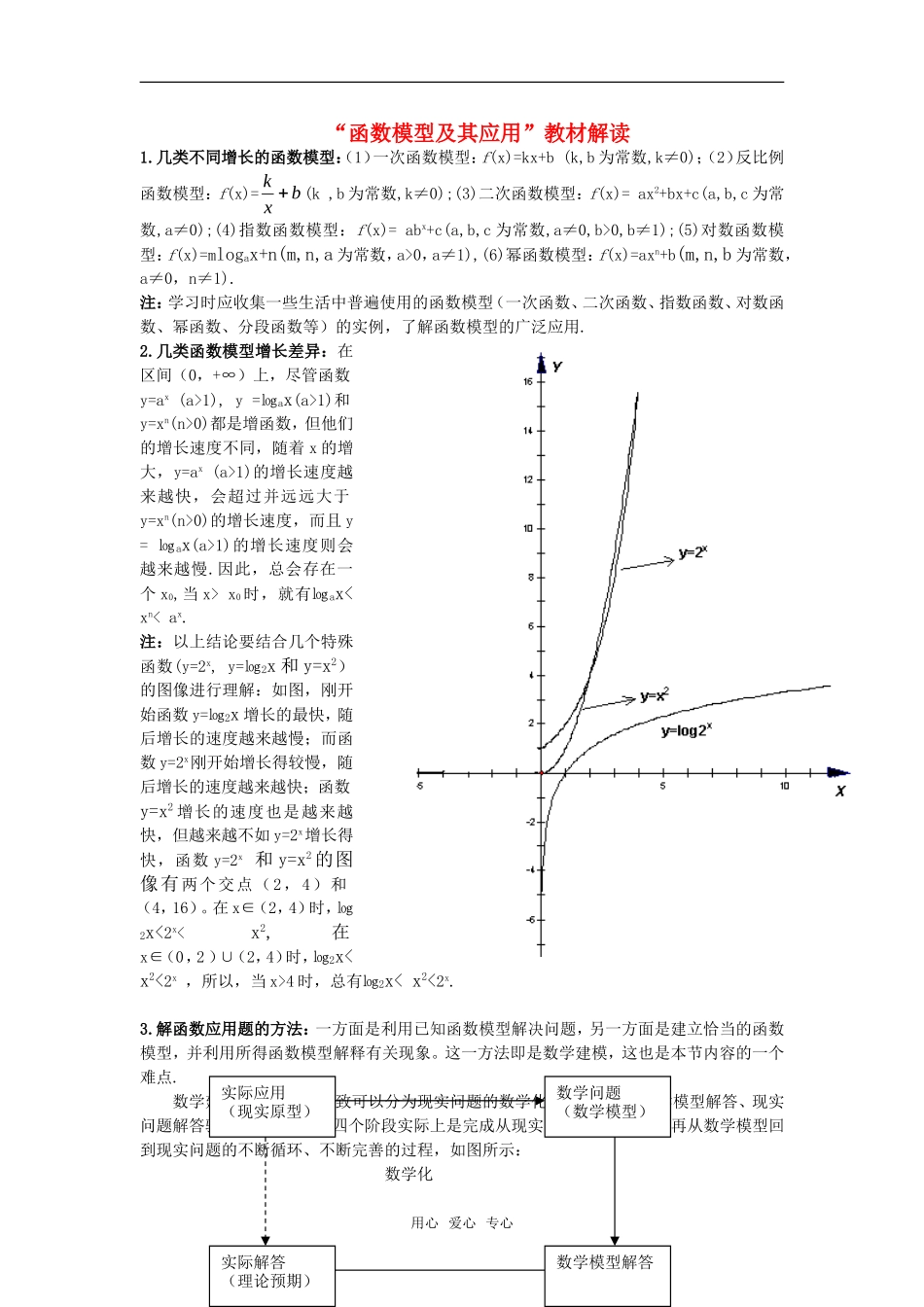
“函数模型及其应用”教材解读1.几类不同增长的函数模型：（1）一次函数模型：f(x)=kx+b(k,b为常数,k≠0)；（2）反比例函数模型：f(x)=bxk(k,b为常数,k≠0);(3)二次函数模型：f(x)=ax2+bx+c(a,b,c为常数,a≠0);(4)指数函数模型：f(x)=abx+c(a,b,c为常数,a≠0,b>0,b≠1);(5)对数函数模型：f(x)=mlogax+n(m,n,a为常数，a>0，a≠1),(6)幂函数模型：f(x)=axn+b(m,n,b为常数，a≠0，n≠1).注：学习时应收集一些生活中普遍使用的函数模型（一次函数、二次函数、指数函数、对数函数、幂函数、分段函数等）的实例，了解函数模型的广泛应用.2.几类函数模型增长差异：在区间（0，+∞）上，尽管函数y=ax(a>1),y=㏒ax(a>1)和y=xn(n>0)都是增函数，但他们的增长速度不同，随着x的增大，y=ax(a>1)的增长速度越来越快，会超过并远远大于y=xn(n>0)的增长速度，而且y=㏒ax(a>1)的增长速度则会越来越慢.因此，总会存在一个x0,当x>x0时，就有㏒ax4时，总有㏒2x