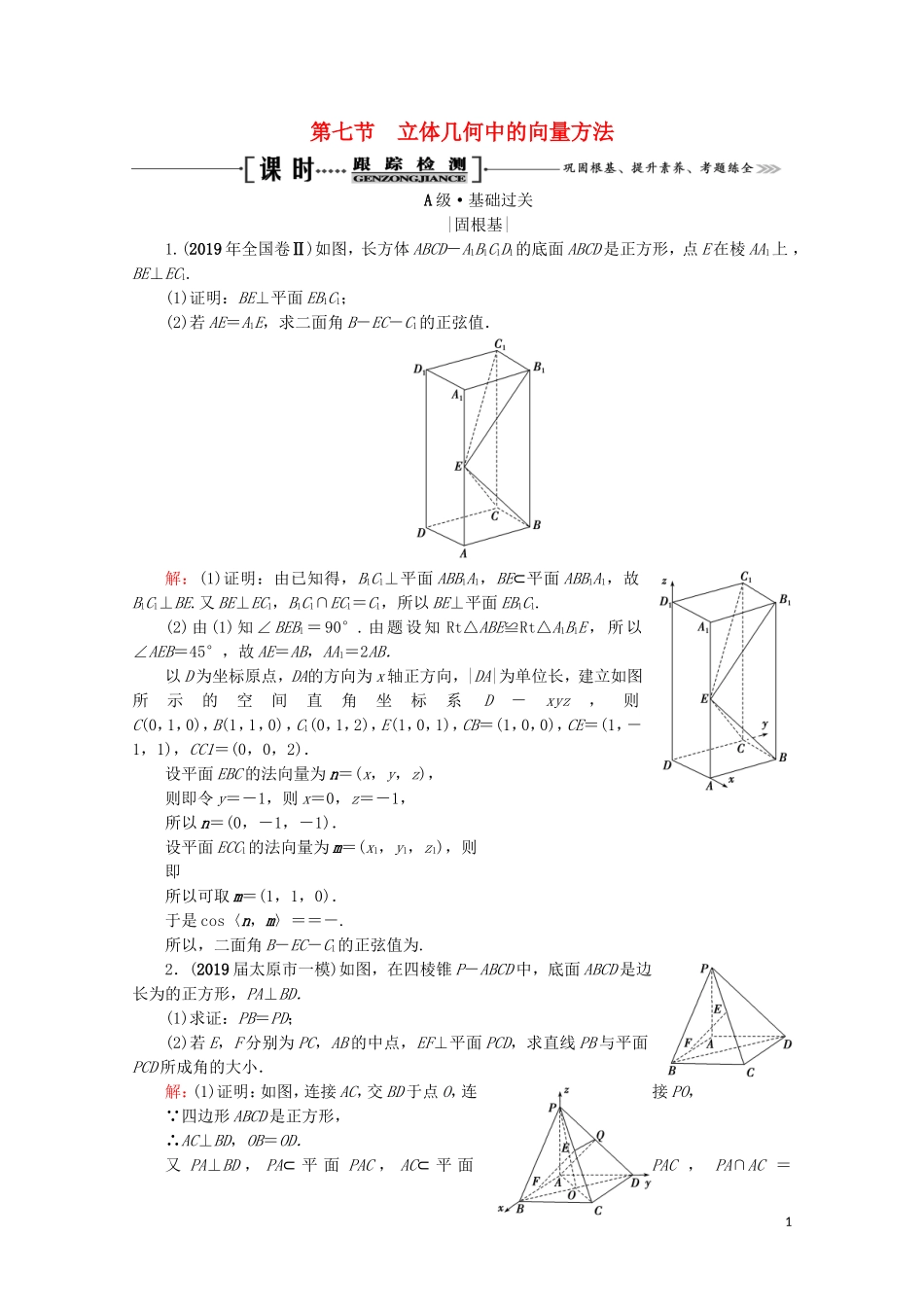
第七节立体几何中的向量方法A级·基础过关|固根基|1.(2019年全国卷Ⅱ)如图,长方体ABCD-A1B1C1D1的底面ABCD是正方形,点E在棱AA1上,BE⊥EC1.(1)证明:BE⊥平面EB1C1;(2)若AE=A1E,求二面角B-EC-C1的正弦值.解:(1)证明:由已知得,B1C1⊥平面ABB1A1,BE⊂平面ABB1A1,故B1C1⊥BE.又BE⊥EC1,B1C1∩EC1=C1,所以BE⊥平面EB1C1.(2)由(1)知∠BEB1=90°.由题设知Rt△ABE≌Rt△A1B1E,所以∠AEB=45°,故AE=AB,AA1=2AB.以D为坐标原点,DA的方向为x轴正方向,|DA|为单位长,建立如图所示的空间直角坐标系D-xyz,则C(0,1,0),B(1,1,0),C1(0,1,2),E(1,0,1),CB=(1,0,0),CE=(1,-1,1),CC1=(0,0,2).设平面EBC的法向量为n=(x,y,z),则即令y=-1,则x=0,z=-1,所以n=(0,-1,-1).设平面ECC1的法向量为m=(x1,y1,z1),则即所以可取m=(1,1,0).于是cos〈n,m〉==-.所以,二面角B-EC-C1的正弦值为.2.(2019届太原市一模)如图,在四棱锥P-ABCD中,底面ABCD是边长为的正方形,PA⊥BD.(1)求证:PB=PD;(2)若E,F分别为PC,AB的中点,EF⊥平面PCD,求直线PB与平面PCD所成角的大小.解:(1)证明:如图,连接AC,交BD于点O,连接PO, 四边形ABCD是正方形,∴AC⊥BD,OB=OD.又PA⊥BD,PA⊂平面PAC,AC⊂平面PAC,PA∩AC=1A,∴BD⊥平面PAC.又PO⊂平面PAC,∴BD⊥PO.又OB=OD,∴PB=PD.(2)设PD的中点为Q,连接AQ,EQ, E为PC的中点,∴EQ∥CD,EQ=CD.又AF∥CD,AB=CD,F为AB的中点,∴AF=AB=CD,∴EQ∥AF,EQ=AF,∴四边形AQEF为平行四边形,∴EF∥AQ. EF⊥平面PCD,∴AQ⊥平面PCD.又PD⊂平面PCD,∴AQ⊥PD. Q是PD的中点,∴AP=AD=. AQ⊥平面PCD,CD⊂平面PCD,∴AQ⊥CD.又AD⊥CD,AQ∩AD=A,∴CD⊥平面PAD.又PA⊂平面PAD,∴CD⊥PA. PA⊥BD,BD∩CD=D,BD⊂平面ABCD,CD⊂平面ABCD,∴PA⊥平面ABCD.以A为坐标原点,以AB,AD,AP所在直线分别为x轴,y轴,z轴,建立如图所示的空间直角坐标系,则A(0,0,0),B(,0,0),P(0,0,),Q,∴AQ=,PB=(,0,-). AQ⊥平面PCD,∴AQ为平面PCD的一个法向量,∴cos〈AQ,PB〉==-.设直线PB与平面PCD所成的角为θ,则sinθ=|cos〈AQ,PB〉|=,∴直线PB与平面PCD所成的角为.3.(2020届广州四校联考)如图1,已知三棱锥P-ABC,其展开图如图2所示,其中四边形ABCD是边长等于的正方形,△ABE和△BCF均为正三角形.(1)证明:平面PAC⊥平面ABC;(2)若M是PA的中点,求二面角P-BC-M的余弦值.解:(1)证明:如图,设AC的中点为O,连接BO,PO.由题意,得PA=PB=PC=,PO=1,AO=BO=CO=1.因为在△PAC中,PA=PC,O为AC的中点,所以PO⊥AC.因为在△POB中,PO=1,OB=1,PB=,所以PO2+OB2=PB2,所以PO⊥OB.因为AC∩OB=O,AC,OB⊂平面ABC,所以PO⊥平面ABC,又PO⊂平面PAC,所以平面PAC⊥平面ABC.(2)由(1)可知PO⊥OB,PO⊥AC,OB⊥AC,所以以O为坐标原点,OC,OB,OP所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系O-xyz,则O(0,0,0),C(1,0,0),B(0,1,0),A(-1,0,0),P(0,0,1),M-,0,,所以BC=(1,-1,0),PC=(1,0,-1),MC=,0,-.2设平面MBC的法向量为m=(x1,y1,z1),则∴令x1=1,得y1=1,z1=3,即m=(1,1,3)为平面MBC的一个法向量.设平面PBC的法向量为n=(x2,y2,z2),则∴令x2=1,得y2=1,z2=1,即n=(1,1,1)为平面PBC的一个法向量.cos〈n,m〉===.由图可知,二面角P-BC-M为锐角,故其余弦值为.B级·素养提升|练能力|4.(2019届辽宁五校联考)如图,在四棱锥E-ABCD中,底面ABCD为直角梯形,其中CD∥AB,BC⊥AB,平面ABE⊥平面ABCD,且AB=AE=BE=2BC=2CD=2,动点F在棱AE上,且EF=λFA.(1)试探究λ的值,使CE∥平面BDF,并给予证明;(2)当λ=1时,求直线CE与平面BDF所成角的正弦值.解:(1)当λ=时,CE∥平面BDF.证明如下:连接AC交BD于点G,连接GF, CD∥AB,AB=2CD,∴==. EF=FA,∴==,∴GF∥CE.又CE⊄平面BDF,GF⊂平面BDF,∴CE∥平面BDF.(2)取AB的中点O,连接EO,则EO⊥AB, 平面...