高考数学一轮复习 第七章 立体几何阶段检测试题（含解析）文-人教版高三全册数学试题VIP免费

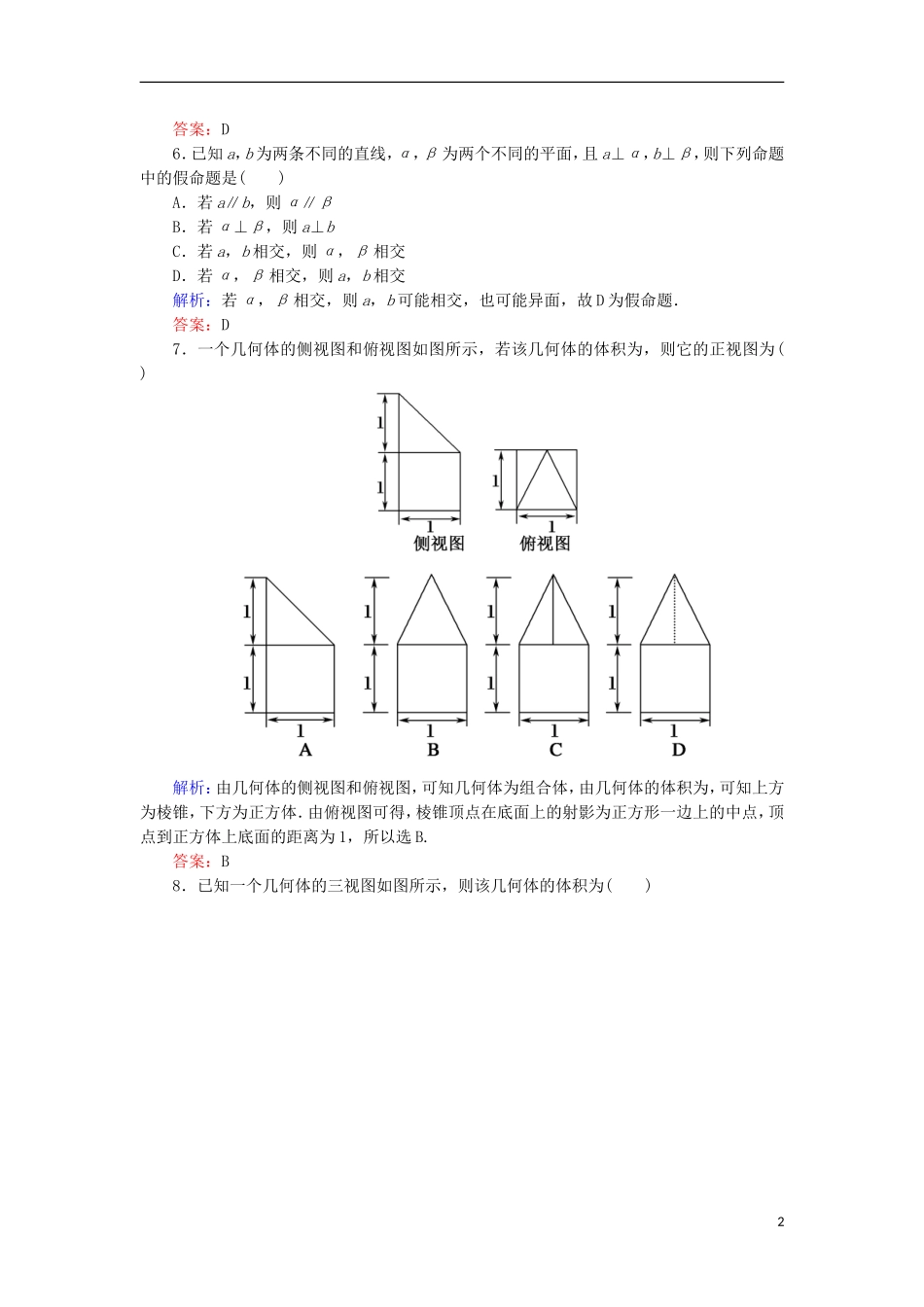
第七章立体几何阶段检测试题时间：120分钟分值：150分一、选择题(每小题5分，共60分)1．关于空间几何体的结构特征，下列说法不正确的是()A．棱柱的侧棱长都相等B．棱锥的侧棱长都相等C．三棱台的上、下底面是相似三角形D．有的棱台的侧棱长都相等解析：根据棱锥的结构特征知，棱锥的侧棱长不一定都相等．答案：B2．在正方体ABCD－A1B1C1D1中，E，F分别是线段BC，CD1的中点，则直线A1B与直线EF的位置关系是()A．相交B．异面C．平行D．垂直解析：由BC綊AD，AD綊A1D1知，BC綊A1D1，从而四边形A1BCD1是平行四边形，所以A1B∥CD1，又EF⊂平面A1C，EF∩D1C＝F，则A1B与EF相交．答案：A3．(2017·嘉兴月考)对于空间的两条直线m，n和一个平面α，下列命题中的真命题是()A．若m∥α，n∥α，则m∥nB．若m∥α，n⊂α，则m∥nC．若m∥α，n⊥α，则m∥nD．若m⊥α，n⊥α，则m∥n解析：对A，直线m，n可能平行、异面或相交，故选项A错误；对B，直线m与n可能平行，也可能异面，故选项B错误；对C，m与n垂直而非平行，故选项C错误；对D，垂直于同一平面的两直线平行，故选项D正确．答案：D4．设P是异面直线a，b外的一点，则过点P与a，b都平行的平面()A．有且只有一个B．恰有两个C．不存在或只有一个D．有无数个解析：过点P作a1∥a，b1∥b，若过a1，b1的平面不经过a，b，则存在一个平面同时与a，b平行；若过a1，b1的平面经过a或b，则不存在这样的平面同时与a，b平行．答案：C5．若平面α∥平面β，点A，C∈α，B，D∈β，则直线AC∥直线BD的充要条件是()A．AB∥CDB．AD∥CBC．AB与CD相交D．A，B，C，D四点共面解析：由平面α∥平面β知，直线AC与BD无公共点，则直线AC∥直线BD的充要条件是A，B，C，D四点共面．1答案：D6．已知a，b为两条不同的直线，α，β为两个不同的平面，且a⊥α，b⊥β，则下列命题中的假命题是()A．若a∥b，则α∥βB．若α⊥β，则a⊥bC．若a，b相交，则α，β相交D．若α，β相交，则a，b相交解析：若α，β相交，则a，b可能相交，也可能异面，故D为假命题．答案：D7．一个几何体的侧视图和俯视图如图所示，若该几何体的体积为，则它的正视图为()解析：由几何体的侧视图和俯视图，可知几何体为组合体，由几何体的体积为，可知上方为棱锥，下方为正方体．由俯视图可得，棱锥顶点在底面上的射影为正方形一边上的中点，顶点到正方体上底面的距离为1，所以选B.答案：B8．已知一个几何体的三视图如图所示，则该几何体的体积为()2A．27－B．18－C．27－3πD．18－3π解析：由几何体的三视图可知该几何体可以看成是底面是梯形的四棱柱挖去了半个圆柱，所以所求体积为×(2＋4)×2×3－π×12×3＝18－.答案：B9．半球内有一个内接正方体，则这个半球的体积与正方体的体积之比为()A.π6B．π2C．π2D．5π12解析：正方体上底面的中心即球的球心，设球的半径为R，正方体的棱长为a，则有R2＝a2＋2，得R2＝a2，所以半球的体积与正方体的体积之比为πR3a3＝π2.答案：B10．如图所示，在直三棱柱ABC－A1B1C1中，BC＝AC，AC1⊥A1B，M，N分别为A1B1，AB的中点．给出下列结论：①C1M⊥平面A1ABB1；②A1B⊥AM；③平面AMC1∥平面CNB1.其中正确结论的个数为()A．0B．1C．2D．3解析：由于ABC－A1B1C1为直三棱柱，所以A1A⊥C1M.由B1C1＝A1C1，M为A1B1的中点，得C1M⊥A1B1.又AA1∩A1B1＝A1，所以C1M⊥平面A1ABB1，所以①正确．因为C1M⊥平面A1ABB1，所以C1M⊥A1B.又AC1⊥A1B，C1M∩AC1＝C1，所以A1B⊥平面AMC1，所以AM⊥A1B，所以②正确．由AM∥B1N，C1M∥CN，可得平面AMC1∥平面CNB1，所以③正确，故正确结论共有3个．答案：D11．如图所示，直线PA垂直于⊙O所在的平面，△ABC内接于⊙O，且AB为⊙O的直径，点3M为线段PB的中点．现有结论：①BC⊥PC；②OM∥平面APC；③点B到平面PAC的距离等于线段BC的长，其中正确的是()A．①②B．①②③C．①D．②③解析：对于①， PA⊥平面ABC，BC⊂平面ABC，∴PA⊥BC. AB为⊙O的直径，∴BC⊥AC，∴BC⊥平面PAC.又PC⊂平面PAC，∴BC⊥PC；对于②， 点M为线段PB的中点，∴OM∥PA. PA⊂平面PAC，∴OM∥平面PAC，对于③，由①知BC⊥平面PAC，∴线段...