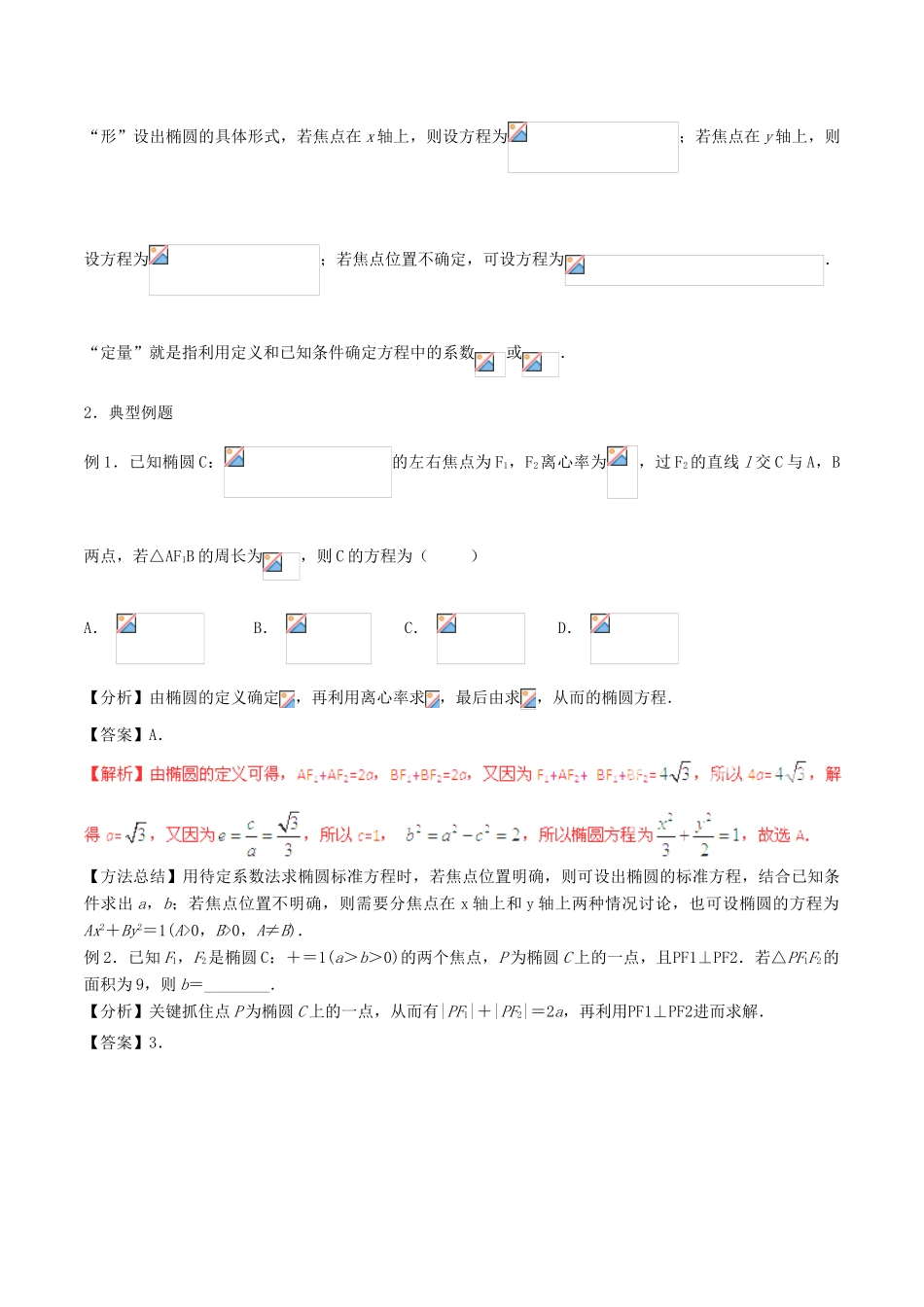
专题13椭圆椭圆的定义与标准方程【背一背基础知识】1.椭圆的定义:平面内与两个定点的距离之和等于常数(大于)的点的轨迹叫做椭圆.这两个定点叫做椭圆的焦点,两焦点间的距离叫做椭圆的焦距.椭圆的定义用符号语言表示:.说明:当时,无轨迹;当时,轨迹为线段.2.椭圆的标准方程:(1)焦点在轴上的椭圆的标准方程:,焦点;(2)焦点在轴上的椭圆的标准方程:,焦点.其中几何意义:表示长轴长的一半,表示短轴长的一半,表示焦距长的一半,并且有.3.椭圆的一般方程:.【讲一讲基本技能】1.必备技能:(1)在高考中,对于椭圆部分内容,在选择题或填空题中一般考查考生椭圆的定义、离心率、焦点坐标等基础知识的掌握情况;解答题中考查考生在求解椭圆的方程、直线与椭圆的位置关系等涉及分析、探求的数学思想的掌握情况.(2)求椭圆的标准方程时,应从“定形”“定式”“定量”三个方面去思考.“定形”就是指椭圆的对称中心在原点,以坐标轴为对称轴的情况下,能否确定椭圆的焦点在x轴还是y轴上.“定式”就是根据“形”设出椭圆的具体形式,若焦点在x轴上,则设方程为;若焦点在y轴上,则设方程为;若焦点位置不确定,可设方程为.“定量”就是指利用定义和已知条件确定方程中的系数或.2.典型例题例1.已知椭圆C:的左右焦点为F1,F2离心率为,过F2的直线l交C与A,B两点,若△AF1B的周长为,则C的方程为()A.B.C.D.【分析】由椭圆的定义确定,再利用离心率求,最后由求,从而的椭圆方程.【答案】A.【方法总结】用待定系数法求椭圆标准方程时,若焦点位置明确,则可设出椭圆的标准方程,结合已知条件求出a,b;若焦点位置不明确,则需要分焦点在x轴上和y轴上两种情况讨论,也可设椭圆的方程为Ax2+By2=1(A>0,B>0,A≠B).例2.已知F1,F2是椭圆C:+=1(a>b>0)的两个焦点,P为椭圆C上的一点,且PF1⊥PF2.若△PF1F2的面积为9,则b=________.【分析】关键抓住点P为椭圆C上的一点,从而有|PF1|+|PF2|=2a,再利用PF1⊥PF2进而求解.【答案】3.【方法总结】椭圆上一点P与椭圆的两焦点组成的三角形通常称为“焦点三角形”,利用定义可求其周长,利用定义和余弦定理可求|PF1|·|PF2|;通过整体代入可求其面积等.例3.已知椭圆C:+=1(a>b>0)的焦距为4,且过点P(,),求椭圆C的方程;【分析】由AE与AD垂直,应转化为AE·AD=0,从而转化为数量的计算.【练一练趁热打铁】1.过点(,-),且与椭圆+=1有相同焦点的椭圆的标准方程为________.【分析】利用定义法或待定系数法求解.【方法总结】(1)求轨迹方程时,先看轨迹的形状能否预知,若能预先知道轨迹为何种圆锥曲线,则可考虑用定义法求解或用待定系数法求解;(2)讨论轨迹方程的解与轨迹上的点是否对应,要注意字母的取值范围.2.已知动点M(x,y)到直线l:x=4的距离是它到点N(1,0)的距离的2倍.(1)求动点M的轨迹C的方程;(2)过点P(0,3)的直线m与轨迹C交于A,B两点,若A是PB的中点,求直线m的斜率.【答案】(1)+=1;(2)-或.将③代入①②,得x1=-,x=,可得()2=,且k2>,解得k=-或k=,∴直线m的斜率为-或.法二:由题意,设直线m的方程为y=kx+3,A(x1,y1),B(x2,y2),如图②. A是PB的中点,∴x1=①y1=.②又+=1,③+=1,④联立①②③④,解得或即点B的坐标为(2,0)或(-2,0),∴直线m的斜率为-或.3.设点P是圆x2+y2=4上任意一点,由点P向x轴作垂线PP0,垂足为P0,且MP0=PP0.求点M的轨迹C的方程;【答案】点M的轨迹C的方程为+=1.椭圆的几何性质【背一背基础知识】椭圆的简单几何性质(以为例):如图1所示,填写各空.(1)范围:.(2)对称性:关于轴、轴以及原点对称,对称轴为轴、轴,对称中心为.(3)顶点:长轴长,短轴长.(4)离心率,.越小,椭圆越圆;越大,椭圆越扁.总结可得如下表格:焦点的位置焦点在轴上焦点在轴上图形标准方程定义到两定点的距离之和等于常数2,即()范围且且顶点轴长长轴的长,短轴的长对称性关于轴、轴对称,关于原点中心对称焦点、、焦距离心率焦点三角形面积弦长公式,【讲一讲基本技能】1.必备技能:讨论椭圆的几何性质时,离心...