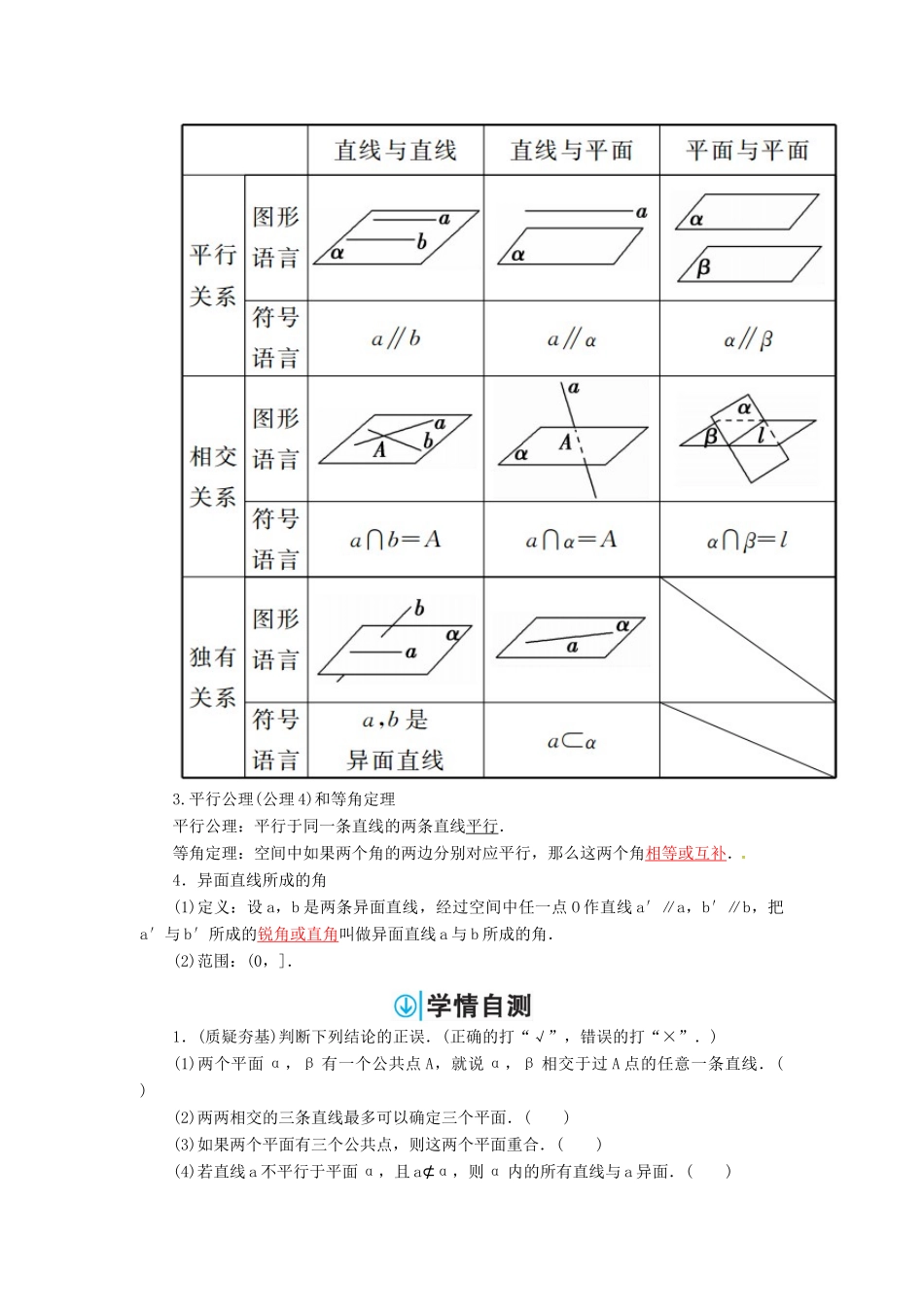
第三节空间点、直线、平面之间的位置关系【最新考纲】1.理解空间直线、平面位置关系的定义.2.了解可以作为推理依据的公理和定理.3.能运用公理、定理和已获得的结论证明一些空间位置关系的简单命题.1.平面的基本性质公理1:如果一条直线上的两点在一个平面内,那么这条直线在这个平面内.公理2:过不共线的三点,有且只有一个平面.公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.2.空间点、直线、平面之间的位置关系3.平行公理(公理4)和等角定理平行公理:平行于同一条直线的两条直线平行.等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补.4.异面直线所成的角(1)定义:设a,b是两条异面直线,经过空间中任一点O作直线a′∥a,b′∥b,把a′与b′所成的锐角或直角叫做异面直线a与b所成的角.(2)范围:(0,].1.(质疑夯基)判断下列结论的正误.(正确的打“√”,错误的打“×”.)(1)两个平面α,β有一个公共点A,就说α,β相交于过A点的任意一条直线.()(2)两两相交的三条直线最多可以确定三个平面.()(3)如果两个平面有三个公共点,则这两个平面重合.()(4)若直线a不平行于平面α,且a⊄α,则α内的所有直线与a异面.()答案:(1)×(2)√(3)×(4)×2.如图所示,在正方体ABCDA1B1C1D1中,E,F分别是AB,AD的中点,则异面直线B1C与EF所成的角的大小为()A.30°B.45°C.60°D.90°解析:连接B1D1,D1C,则B1D1∥EF,故∠D1B1C为所求,又B1D1=B1C=D1C,∴∠D1B1C=60°.答案:C3.(经典再现)在下列命题中,不是公理的是()A.平行于同一个平面的两个平面相互平行B.过不在同一条直线上的三点,有且只有一个平面C.如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内D.如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线解析:A不是公理,是个常用的结论,需经过推理论证;B,C,D是平面的基本性质公理.答案:A4.(2015·广东卷)若直线l1和l2是异面直线,l1在平面α内,l2在平面β内,l是平面α与平面β的交线,则下列命题正确的是()A.l与l1,l2都不相交B.l与l1,l2都相交C.l至多与l1,l2中的一条相交D.l至少与l1,l2中的一条相交解析:法一 l与l1,l2分别共面.故直线l与l1,l2要么都不相交,要么至少与l1,l2中的一条相交.若l∥l1,l∥l2,则l1∥l2,这与l1,l2是异面直线矛盾.故l至少与l1,l2中的一条相交.法二如图1,l1与l2是异面直线,l1与l平行,l2与l相交,故A,B不正确;如图2,l1与l2是异面直线,l1,l2都与l相交,故C不正确.答案:D5.已知正方体ABCDA1B1C1D1中,E、F分别为BB1、CC1的中点,那么异面直线AE与D1F所成角的余弦值为________.解析:连接DF,则AE∥DF,∴∠D1FD为异面直线AE与D1F所成的角.设正方体棱长为a,则D1D=a,DF=a,D1F=a,∴cos∠D1FD==.答案:两点注意1.异面直线不同在任何一个平面内,不能错误地理解为不在某一个平面内的两条直线就是异面直线.2.直线与平面的位置关系在判断时最易忽视“线在面内”.两种方法异面直线的判定方法:1.判定定理:平面外一点A与平面内一点B的连线和平面内不经过该点的直线是异面直线.2.反证法:证明两直线不可能平行、相交或证明两直线不可能共面,从而可得出两直线异面.三个作用1.公理1的作用:(1)判断直线在平面内;(2)由直线在平面内判断直线上的点在平面内;(3)由直线的“直”刻画平面的平.2.公理2的作用:公理2及其推论给出了确定一个平面或判断直线共面的方法.3.公理3的作用:(1)判定两平面相交;(2)作两平面相交的交线;(3)证明多点共线.A级基础巩固一、选择题1.给出以下命题:①不共面的四点中,其中任意三点不共线;②若点A,B,C,D共面,点A,B,C,E共面,则点A,B,C,D,E共面;③若直线a,b共面,直线a,c共面,则直线b,c共面;④依次首尾相接的四条线段必共面.正确命题的个数是()A.0B.1C.2D.3解析:①中显然是正确的;②中若A,B,C三点共线则A,B,C,D,E五点不一定共面,不正确;③构造长方体或正方体,如图显然b、c异面故不正确;④...