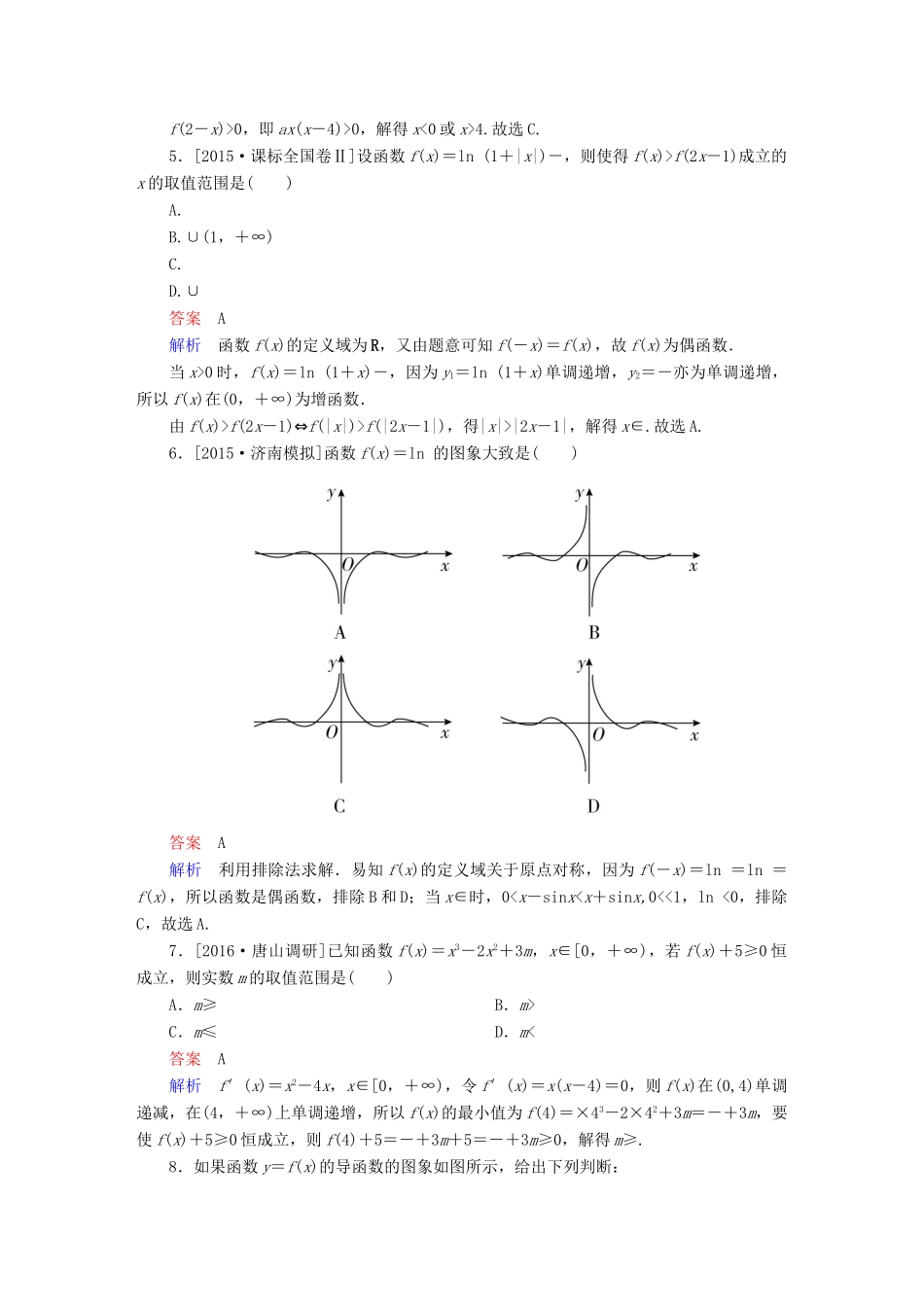
2017年高考分段测试(一)(测试范围:集合与常用逻辑用语函数、导数及其应用)时间:120分钟满分:150分一、选择题(共12小题,每小题5分,共60分)1.[2015·江西九江一模]若集合A={x|1≤3x≤81},B={x|log2(x2-x)>1},则A∩B=()A.(2,4]B.[2,4]C.(-∞,0)∪(0,4]D.(-∞,-1)∪[0,4]答案A解析因为A={x|1≤3x≤81}={x|30≤3x≤34}={x|0≤x≤4},B={x|log2(x2-x)>1}={x|x2-x>2}={x|x<-1或x>2},所以A∩B={x|0≤x≤4}∩{x|x<-1或x>2}={x|20,且a≠1)在R上为增函数;p2:∃a,b∈R,a2-ab+b2<0;p3:cosα=cosβ成立的一个充分不必要条件是α=2kπ+β(k∈Z).则下列命题中的真命题为()A.p1∨p2B.p2∧p3C.p1∨(綈p3)D.(綈p2)∧p3答案D解析对于p1,令f(x)=ax+x(a>0,且a≠1),当a=时,f(0)=0+0=1,f(-1)=-1-1=1,所以p1为假命题;对于p2,因为a2-ab+b2=2+b2≥0,所以p2为假命题;对于p3,因为cosα=cosβ⇔α=2kπ±β(k∈Z),所以p3是真命题,所以(綈p2)∧p3为真命题,故选D.4.[2015·山东威海一模]函数f(x)=(x-2)(ax+b)为偶函数,且在(0,+∞)上单调递增,则f(2-x)>0的解集为()A.{x|x>2或x<-2}B.{x|-24}D.{x|00.f(2-x)>0,即ax(x-4)>0,解得x<0或x>4.故选C.5.[2015·课标全国卷Ⅱ]设函数f(x)=ln(1+|x|)-,则使得f(x)>f(2x-1)成立的x的取值范围是()A.B.∪(1,+∞)C.D.∪答案A解析函数f(x)的定义域为R,又由题意可知f(-x)=f(x),故f(x)为偶函数.当x>0时,f(x)=ln(1+x)-,因为y1=ln(1+x)单调递增,y2=-亦为单调递增,所以f(x)在(0,+∞)为增函数.由f(x)>f(2x-1)⇔f(|x|)>f(|2x-1|),得|x|>|2x-1|,解得x∈.故选A.6.[2015·济南模拟]函数f(x)=ln的图象大致是()答案A解析利用排除法求解.易知f(x)的定义域关于原点对称,因为f(-x)=ln=ln=f(x),所以函数是偶函数,排除B和D;当x∈时,0C.m≤D.m<答案A解析f′(x)=x2-4x,x∈[0,+∞),令f′(x)=x(x-4)=0,则f(x)在(0,4)单调递减,在(4,+∞)上单调递增,所以f(x)的最小值为f(4)=×43-2×42+3m=-+3m,要使f(x)+5≥0恒成立,则f(4)+5=-+3m+5=-+3m≥0,解得m≥.8.如果函数y=f(x)的导函数的图象如图所示,给出下列判断:①函数y=f(x)在区间内单调递增;②函数y=f(x)在区间内单调递减;③函数y=f(x)在区间(4,5)内单调递增;④当x=2时,函数y=f(x)有极小值;⑤当x=-时,函数y=f(x)有极大值.则上述判断中正确的是()A.①②B.②③C.③④⑤D.③答案D解析当x∈(-3,-2)时,f′(x)<0,f(x)单调递减,①错;当x∈时,f′(x)>0,f(x)单调递增,当x∈(2,3)时,f′(x)<0,f(x)单调递减,②错;当x=2时,函数y=f(x)有极大值,④错;当x=-时,函数y=f(x)无极值,⑤错.故选D.9.f(x)=2sinπx-x+1的零点个数为()A.4B.5C.6D.7答案B解析 2sinπx-x+1=0,∴2sinπx=x-1.令h(x)=2sinπx,g(x)=x-1,f(x)=2sinπx-x+1的零点个数转化为求两个函数图象的交点个数.h(x)=2sinπx的周期T==2,分别画出两个函数的图象,如图所示, h(1)=g(1),h>g,g(4)=3>2,g(-2)=-3<-2,可知两个函数图象的交点一共5个,∴f(x)=2sinπx-x+1的零点个数为5.10.记定义在R上的可导函数f(x),如果存在x0∈[a...