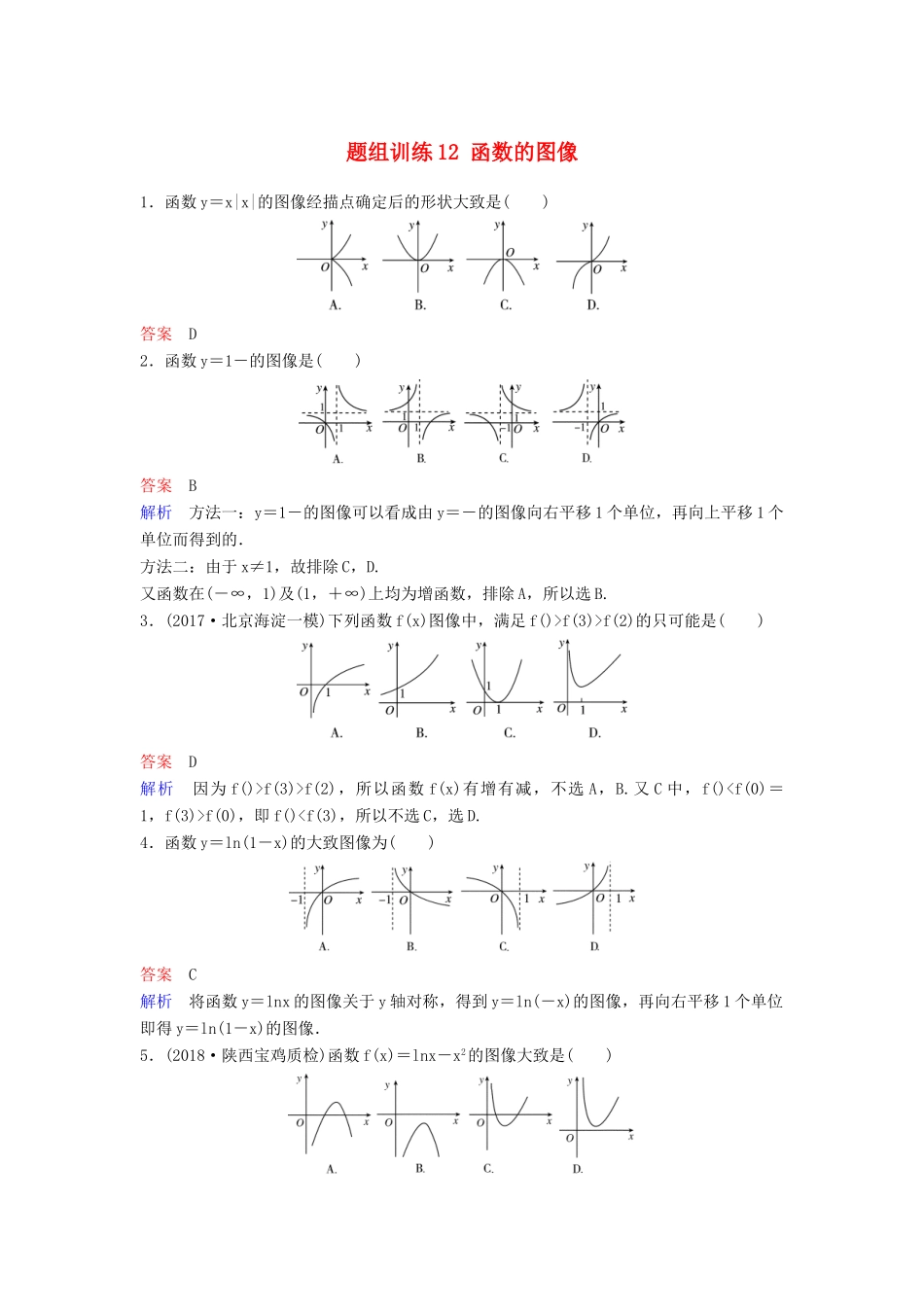
题组训练12函数的图像1.函数y=x|x|的图像经描点确定后的形状大致是()答案D2.函数y=1-的图像是()答案B解析方法一:y=1-的图像可以看成由y=-的图像向右平移1个单位,再向上平移1个单位而得到的.方法二:由于x≠1,故排除C,D.又函数在(-∞,1)及(1,+∞)上均为增函数,排除A,所以选B.3.(2017·北京海淀一模)下列函数f(x)图像中,满足f()>f(3)>f(2)的只可能是()答案D解析因为f()>f(3)>f(2),所以函数f(x)有增有减,不选A,B.又C中,f()f(0),即f()0,函数单调递增;在x∈(1,+∞)时,f′(x)<0,函数单调递减.故x=1为极大值点,f(1)=-<0,故选B.6.函数f(x)=xsinx的图像大致是()答案A解析因为f(-x)=-xsin(-x)=xsinx=f(x),所以函数f(x)为偶函数,所以其图像关于y轴对称,故排除B,C;因为f(π)=πsinπ=0,排除D,故选A.7.(2017·华东师大附中调研)若函数y=f(x)的图像上的任意一点P的坐标(x,y)满足条件|x|≥|y|,则称函数f(x)具有性质S,那么下列函数中具有性质S的是()A.f(x)=ex-1B.f(x)=ln(x+1)C.f(x)=sinxD.f(x)=tanx答案C解析不等式|x|≥|y|表示的平面区域如图所示,函数f(x)具有性质S,则函数图像必须完全分布在阴影区域①和②部分,f(x)=ex-1的图像分布在区域①和③内,f(x)=ln(x+1)的图像分布在区域②和④内,f(x)=sinx的图像分布在区域①和②内,f(x)=tanx在每个区域都有图像,故选C.8.已知lga+lgb=0,函数f(x)=ax与函数g(x)=-logbx的图像可能是()答案B解析 lga+lgb=0,∴lgab=0,ab=1,∴b=.∴g(x)=-logbx=logax,∴函数f(x)与g(x)互为反函数,图像关于直线y=x对称,故选B.9.(2018·衡水中学调研卷)为了得到函数y=lg的图像,只需把函数y=lgx的图像上所有的点()A.向左平移3个单位长度,再向上平移1个单位长度B.向右平移3个单位长度,再向上平移1个单位长度C.向左平移3个单位长度,再向下平移1个单位长度D.向右平移3个单位长度,再向下平移1个单位长度答案C解析 y=lg=lg(x+3)-1.∴选C.10.函数f(x)=的图像关于()A.原点对称B.直线y=x对称C.直线y=-x对称D.y轴对称答案A解析由题意可知,函数f(x)的定义域为R,且f(x)==2x-2-x,f(-x)=2-x-2x=-f(x),所以函数f(x)为奇函数,故选A.11.(2018·《高考调研》原创题)已知函数y=f(x)(x∈R)的图像如图所示,给出下列四个命题:p1:函数y=f(x)满足f(-x)=-f(x);p2:函数y=f(x)满足f(x+2)=f(-x);p3:函数y=f(x)满足f(x)=f(-x);p4:函数y=f(x)满足f(x+2)=f(x),其中的真命题是()A.p1,p3B.p2,p4C.p1,p2D.p3,p4答案C解析从函数图像上可以看出函数的图像关于原点对称,所以是奇函数,函数y=f(x)满足f(-x)=-f(x),p1为真命题,p3为假命题;从函数图像上可以看出函数的周期为4,由p2:f(x+2)=f(-x)=-f(x),即f(x+4)=f(x),知函数的周期为4,所以p2为真命题,p4为假命题,选择C.12.现有四个函数①y=x·sinx,②y=x·cosx,③y=x·|cosx|,④y=x·2x的部分图像如下,但顺序被打乱,则按照图像从左到右的顺序,对应的函数序号正确的一组是()A.①④②③B.①④③②C.④①②③D.③④②①答案A解析①y=x·sinx在定义域上是偶函数,其图像关于y轴对称;②y=x·cosx在定义域上是奇函数,其图像关于原点对称;③y=x·|cosx|在定义域上是奇函数,其图像关于原点对称,且当x>0时,其函数值y≥0;④y=x·2x在定义域上为非奇非偶函数,且当x>0时,其函数值y>0,且当x<0时,其函数值y<0.故选A.13.已知下图①的图像对应的函数为y=f(x),则图②的图像对应的函数在下列给出的四式中,只可能是()A.y=f(|x|)B.y=|f(x)|C.y=f(-|x|)D.y=-f(|x|)答案C14.(2018·安徽毛坦厂中学模拟)已知...