9三角函数的简单应用--北师大必修4VIP免费

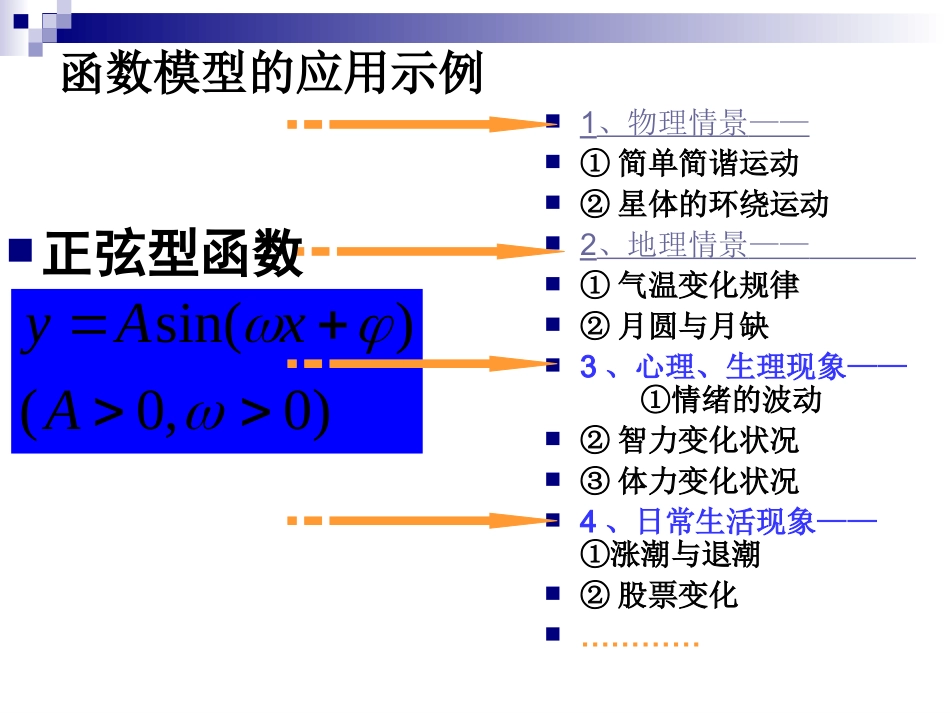
三角函数的简单应用函数模型的应用示例1、物理情景——①简单简谐运动②星体的环绕运动2、地理情景——①气温变化规律②月圆与月缺3、心理、生理现象——①情绪的波动②智力变化状况③体力变化状况4、日常生活现象——①涨潮与退潮②股票变化…………)0,0()sin(AxAy正弦型函数sin()(0,0)yAxA振幅初相（x=0时的相位）相位2:T周期1:2fT频率水车问题1.5m,R1.2mb()40QOPttrad240radsTsin()hPMPNNMRb1.2sin1.553.10.2951.5sin(0.295)1.2(m)40ht1.2-0.31.22.71.291.871.851.831.811.8t)(2.1)295.040sin(5.1mthh/mt/s11.831.851.871.891.81.22.7-0.3例1下图是某简谐运动的图象，试根据图象回答下列问题：（1）这个简谐运动的振幅、周期与频率各是多少？（2）从O点算起，到曲线上的哪一点，表示完成了一次往复运动？如从A点算起呢？（3）写出这个简谐运动的函数表达式。OA2BCDFEy/cmx/s0.40.81.22A0.8Ts1.25fDE52sin2yx例2如果某地夏天从8~14时用电量变化曲线近似满足函数y=Asin(ωx+)+b,如图所示.(1)求这一天的最大用电量和最小用电量;(2)写出这段曲线的函数解析式.解:(1)观察图象知这一题中的最大用电量为50万度,最小用电量为30万度.(2)观察图象可知,半个周期为12,T1486T12.2,6T()40.6y10sinx11(5030)40,(5030)10,22bA.6,x8y30将代入上式解得()66,8,14xy10sin40x所求解析式为规律技巧:确定函数关系式y=Asin(ωx+)就是确定其中的参数A､ω､等,从图象的特征上找答案,A主要由最值确定,ω是由周期确定,周期T通过特殊点观察图象求得,如相邻的最大值,最小值相差半个周期,又由图象上的点求得,确定值时,要注意它的不惟一性,一般求||中最小的.)sin(tAI,0,0Ats1001练习已知电流与时间关系的图像如下图所示，写出解析式；在任意一段最小值，需进行调整，求调整后正整数ω的最小值是多少？。为了使的时间内电流能同时取得最大值和【解】由图像可知，)100sin(3001002501)1501601(2,300tITTA10300把(-，)代入可得3)3100sin(300tI故得：在任意一段s1001的时间内，电流能同时取得最大、最小值，说明s1001不小于一个周期，即,Z20021001，的最小值为629.交流电的电压E(单位：V)与时间t(单位：s)的关系可用E＝2203·sin(100πt＋π6)来表示，求：(1)开始时电压；(2)电压值重复出现一次的时间间隔；(3)电压的最大值和第一次获得最大值的时间．例3.【思路点拨】交流电压与时间的关系呈现周期性变化，t＝0时即为初始电压，求周期和最值可直接运用三角函数性质．(1)0E=110(V).t3当时，【解】110V.3即开始时的电压为21==..10050T2002s(s)，即时间间隔为162300tt100πs当+=，即＝时第一次取得最大值．3.3220V电压的最大值为例4受日月引力,海水会发生涨落,在通常情况下,船在涨潮时驶进航道,靠近船坞;卸货后落潮时返回海洋,某港口水的深度y(m)是时间t(0≤t≤24,单位:h)的函数,记作y=f(t),下面是该港口在某季节每天水深的数据:经长期观察,y=f(t)曲线可以近似地看做函数y=Asinωt+k的图象.t(h)03691215182124y(m)10.013.09.97.010.013.010.17.010.0(1)根据以上数据,求出函数y=f(t)的近似表达式;(2)一般情况下,船舶航行时,船底离海底的距离为5m或5m以上认为是安全的(船舶停靠时,船底只需不碰海底即可),某船吃水深度(船底离水面距离)为6.5m.如果该船在同一天内安全进出港,问它至多能在港内停留多长时间(忽略进出港所需的时间)?分析:可先根据给出的数据在坐标系中作出散点图,再结合几点关键数据求出解析式,最后解决实际问题.解:(1)根据数据画出散点图,如下图,则周期T=12,振幅A=3,k=10,y=3sint+10(0≤t≤24).∴6(),,..,2565115m由题意该船进出港时水深应不小于131011.5,,662sintsint即≥≥5666(),,t...