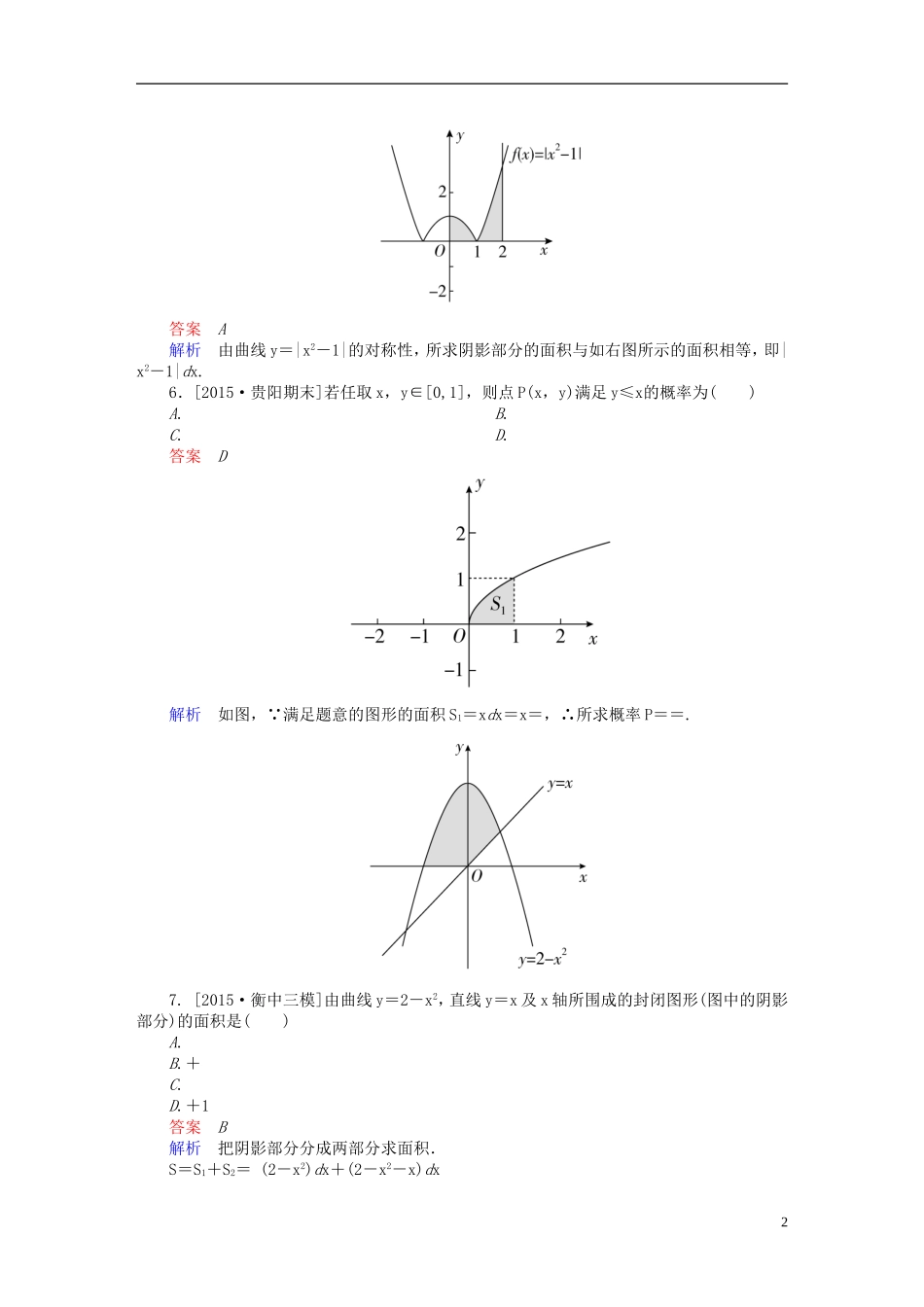
第二章函数、导数及其应用2.12定积分与微积分基本定理练习理[A组·基础达标练]1.与定积分∫dx相等的是()A.∫sindxB.∫dxC.D.以上结论都不对答案B解析 1-cosx=2sin2,∴∫dx=∫dx=·∫dx.2.[2016·开封考试]若∫(x2+mx)dx=0,则实数m的值为()A.-B.-C.-1D.-2答案B解析由题意知,∫(x2+mx)dx==+=0,得m=-.3.[2015·山西四校联考]定积分|x2-2x|dx=()A.5B.6C.7D.8答案D解析|x2-2x|=|x2-2x|dx=(x2-2x)dx+(-x2+2x)dx=+=8.4.[2015·洛阳统考]利用计算机产生0~1之间的均匀随机数a,则事件“0x2dx>”发生的概率为()A.B.C.D.答案C解析 x2dx=x3=a3>,∴a>,∴P==.5.[2015·淄博一模]如图所示,曲线y=x2-1,x=2,x=0,y=0围成的阴影部分的面积为()A.|x2-1|dxB.C.(x2-1)dxD.(x2-1)dx+(1-x2)dx1答案A解析由曲线y=|x2-1|的对称性,所求阴影部分的面积与如右图所示的面积相等,即|x2-1|dx.6.[2015·贵阳期末]若任取x,y∈[0,1],则点P(x,y)满足y≤x的概率为()A.B.C.D.答案D解析如图, 满足题意的图形的面积S1=xdx=x=,∴所求概率P==.7.[2015·衡中三模]由曲线y=2-x2,直线y=x及x轴所围成的封闭图形(图中的阴影部分)的面积是()A.B.+C.D.+1答案B解析把阴影部分分成两部分求面积.S=S1+S2=(2-x2)dx+(2-x2-x)dx2=+=2-+2--=+.8.[2014·湖北高考]若函数f(x),g(x)满足f(x)g(x)dx=0,则称f(x),g(x)为区间[-1,1]上的一组正交函数.给出三组函数:①f(x)=sinx,g(x)=cosx;②f(x)=x+1,g(x)=x-1;③f(x)=x,g(x)=x2.其中为区间[-1,1]上的正交函数的组数是()A.0B.1C.2D.3答案C解析对于①,sinxcosxdx=sinxdx=0,所以①是一组正交函数;对于②,(x+1)(x-1)dx=(x2-1)dx≠0,所以②不是一组正交函数;对于③,x·x2dx=x3dx=0,所以③是一组正交函数.选C.9.[2015·合肥模拟]设函数f(x)=(x-1)x(x+1),则满足f′(x)dx=0的实数a=________.答案1解析f′(x)dx=f(a)=0,得a=0或1或-1,又由积分性质知a>0,故a=1.10.sindx=________.答案2解析依题意得sindx=(sinx+cosx)dx=(sinx-cosx)=-(sin0-cos0)=2.11.已知f(x)为二次函数,且f(-1)=2,f′(0)=0,f(x)dx=-2,(1)求f(x)的解析式;(2)求f(x)在[-1,1]上的最大值与最小值.解(1)设f(x)=ax2+bx+c(a≠0),则f′(x)=2ax+b.由f(-1)=2,f′(0)=0,得即∴f(x)=ax2+2-a.又f(x)dx=(ax2+2-a)dx==2-a=-2,∴a=6,从而f(x)=6x2-4.(2) f(x)=6x2-4,x∈[-1,1].∴当x=0时,[f(x)]min=-4;当x=±1时,[f(x)]max=2.12.在区间[0,1]上给定曲线y=x2.试在此区间内确定点t的值,使图中的阴影部分的面3积S1与S2之和最小,并求最小值.解S1面积等于边长分别为t与t2的矩形面积去掉曲线y=x2与x轴、直线x=t所围成的面积,即S1=t·t2-x2dx=t3.S2的面积等于曲线y=x2与x轴,x=t,x=1围成的面积去掉矩形边长分别为t2,1-t面积,即S2=x2dx-t2(1-t)=t3-t2+.所以阴影部分的面积S(t)=S1+S2=t3-t2+(0≤t≤1).令S′(t)=4t2-2t=4t=0,得t=0或t=.t=0时,S(t)=;t=时,S(t)=;t=1时,S(t)=.所以当t=时,S(t)最小,且最小值为.[B组·能力提升练]1.如图所示,在边长为1的正方形OABC中任取一点P,则点P恰好取自阴影部分的概率为()A.B.C.D.答案C解析根据题意,正方形OABC的面积为1×1=1,而阴影部分由函数y=x与y=围成,其面积为(-x)dx==,则在正方形OABC中任取一点P,点P恰好取自阴影部分的概率为=.故应选C.2.由曲线y=sinx,y=cosx与直线x=0,x=所围成的平面图形(如图中的阴影部分所示)的面积是()A.1B.C.D.2-2答案D解析解法一:由sinx=cosx,得x=.故所求阴影部分的面积S=(cosx-sinx)dx+(sinx-cosx)dx=(sinx+cosx)+(-cosx-sinx)=sin+cos-sin0-cos0+=2-2.故选D.解法二:由sinx=cosx,得x=.根据图象的对称性,可知所求阴影部分的面积4S=2(cosx-sinx)dx=2(sinx+cosx)=2=2-2.故选D.3.设函数f(x)=ax2+c(a≠0),若f(x)dx=f(x0),0≤x0≤1,则x0的值...