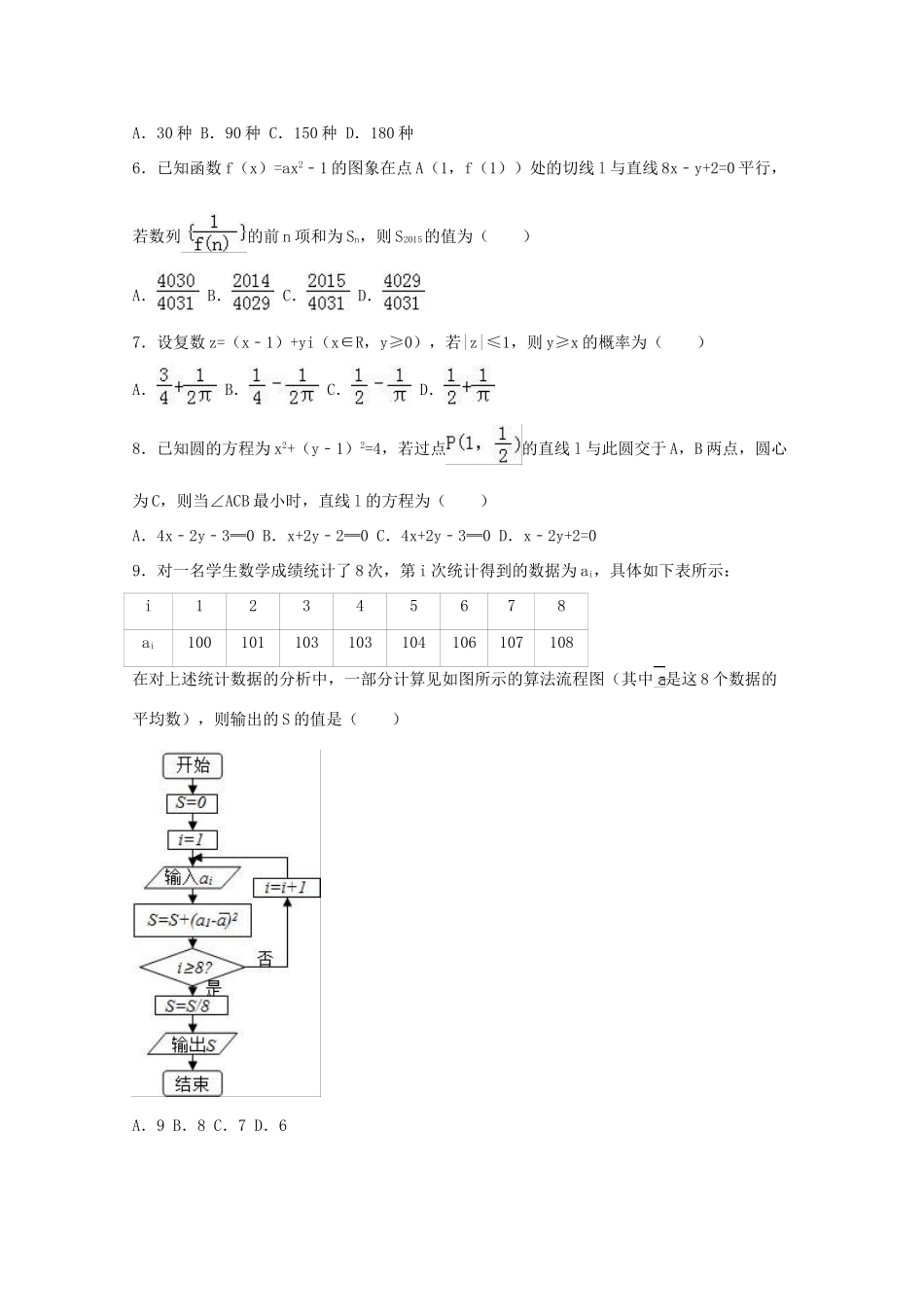
2016年陕西省西安市西工大附中高考数学二模试卷(理科)一、选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.抛物线y=3x2的焦点坐标是()A.B.C.D.2.《莱因德纸草书》(RhindPapyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的是较小的两份之和,问最小一份为()A.B.C.D.3.下列命题中,假命题是()A.“π是函数y=sinx的一个周期”或“2π是函数y=cosx的一个周期”B.“m>0”是“函数f(x)=m+log2x(x≥1)不存在零点”的充分不必要条件C.“若a≤b,则2a≤2b﹣1”的否命题D.“任意a∈(0,+∞),函数y=ax在定义域内单调递增”的否定4.如图是一个有底的容器的三视图,现向容器中匀速注水,容器中水面的高度随时间变化的可能图象是()A.B.C.D.5.某中学数学组来了5名即将毕业的大学生进行教学实习活动,现将他们分配到高一年级的1,2,3三个班实习,每班至少一名,最多两名,则不同的分配方案有()A.30种B.90种C.150种D.180种6.已知函数f(x)=ax2﹣1的图象在点A(1,f(1))处的切线l与直线8x﹣y+2=0平行,若数列的前n项和为Sn,则S2015的值为()A.B.C.D.7.设复数z=(x﹣1)+yi(x∈R,y≥0),若|z|≤1,则y≥x的概率为()A.B.C.D.8.已知圆的方程为x2+(y﹣1)2=4,若过点的直线l与此圆交于A,B两点,圆心为C,则当∠ACB最小时,直线l的方程为()A.4x﹣2y﹣3═0B.x+2y﹣2═0C.4x+2y﹣3═0D.x﹣2y+2=09.对一名学生数学成绩统计了8次,第i次统计得到的数据为ai,具体如下表所示:i12345678ai100101103103104106107108在对上述统计数据的分析中,一部分计算见如图所示的算法流程图(其中是这8个数据的平均数),则输出的S的值是()A.9B.8C.7D.610.已知⊥,||=,||=t,t∈[,4];若P是△ABC所在平面内一点,且=+,则的取值范围是()A.B.C.[,12]D.[,13]11.已知定义在(n∈N*)时,函数f(x)的图象与x轴围成的图象面积为Sn,则Sn=()A.nB.2C.2nD.12.已知数列{an}满足a1=1,a2=,且an+2﹣2an+2=0,0∈N*,记T2n为数列{an}的前2n项和,数列{bn}是首项和公比都是2的等比数列,则使不等式(T2n+)•<1成立的最小整数n为()A.7B.6C.5D.4二、填空题:本大题共4小题,每小题5分.13.在△ABC中,角A,B,C所对边的长分别为a,b,c,已知b=c,sinA+sinC=2sinB,则cosA=.14.已知集合,且(∁RB)∪A=R,则实数a的取值范围是.15.二项式的展开式中所有有理项的系数和等于(用数字作答).16.已知点A(a,b)与点B(1,0)在直线3x﹣4y+10=0的两侧,给出下列说法:①3a﹣4b+10>0;②当a>0时,a+b有最小值,无最大值;③>2;④当a>0且a≠1,b>0时,的取值范围为(﹣∞,﹣)∪(,+∞).其中,所有正确说法的序号是.三、解答题:解答应写出文字说明、证明过程或演算步骤.17.已知函数f(x)=sin(2x+)+sin(2x﹣)﹣cos2x+a(a∈R,a为常数).(1)求函数f(x)的最小正周期和单调增区间;(2)若函数f(x)的图象向左平移m(m>0)个单位后,得到函数g(x)的图象关于y轴对称,求实数m的最小值.18.如图直三棱柱ABC﹣A1B1C1中,AC=CC1=2,AB=BC,D是BA1上一点,且AD⊥平面A1BC.(1)求证:BC⊥平面ABB1A1;(2)在棱BB1是否存在一点E,使平面AEC与平面ABB1A1的夹角等于60°,若存在,试确定E点的位置,若不存在,请说明理由.19.第二届世界互联网大会将于2015年12月16日﹣18日在浙江乌镇进行,届时将有世界各国的互联网精英云集于此共商世界互联网的未来.现在人们的生活已经离不开互联网,网上购物已悄悄走进人们的生活,在刚刚过去的双十一,有4位好友相约:每个人通过执一枚质地均匀的骰子决定自己去哪家购物,掷出点数为5或6的人去淘宝购物,掷出点数小于5的人去京东商城购物,且参加者必须从淘宝网和京东商城选择一家购物.(1)求这4个人中恰有1人去淘宝网购物的概率;(2)用ξ,η本别表示这4个人中去淘宝网和京东商城购物的人数,记X=ξη,求随机变量X分...