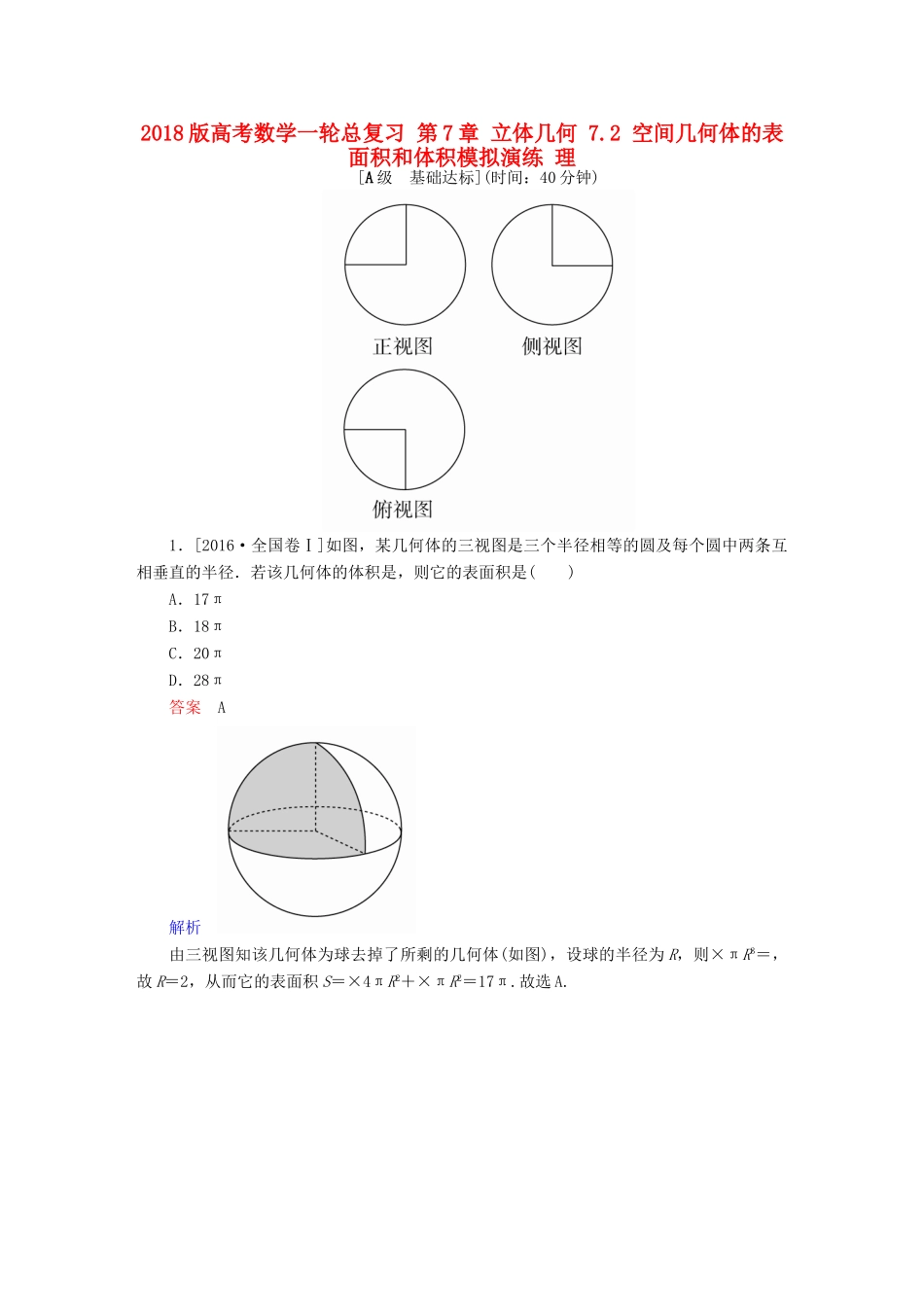
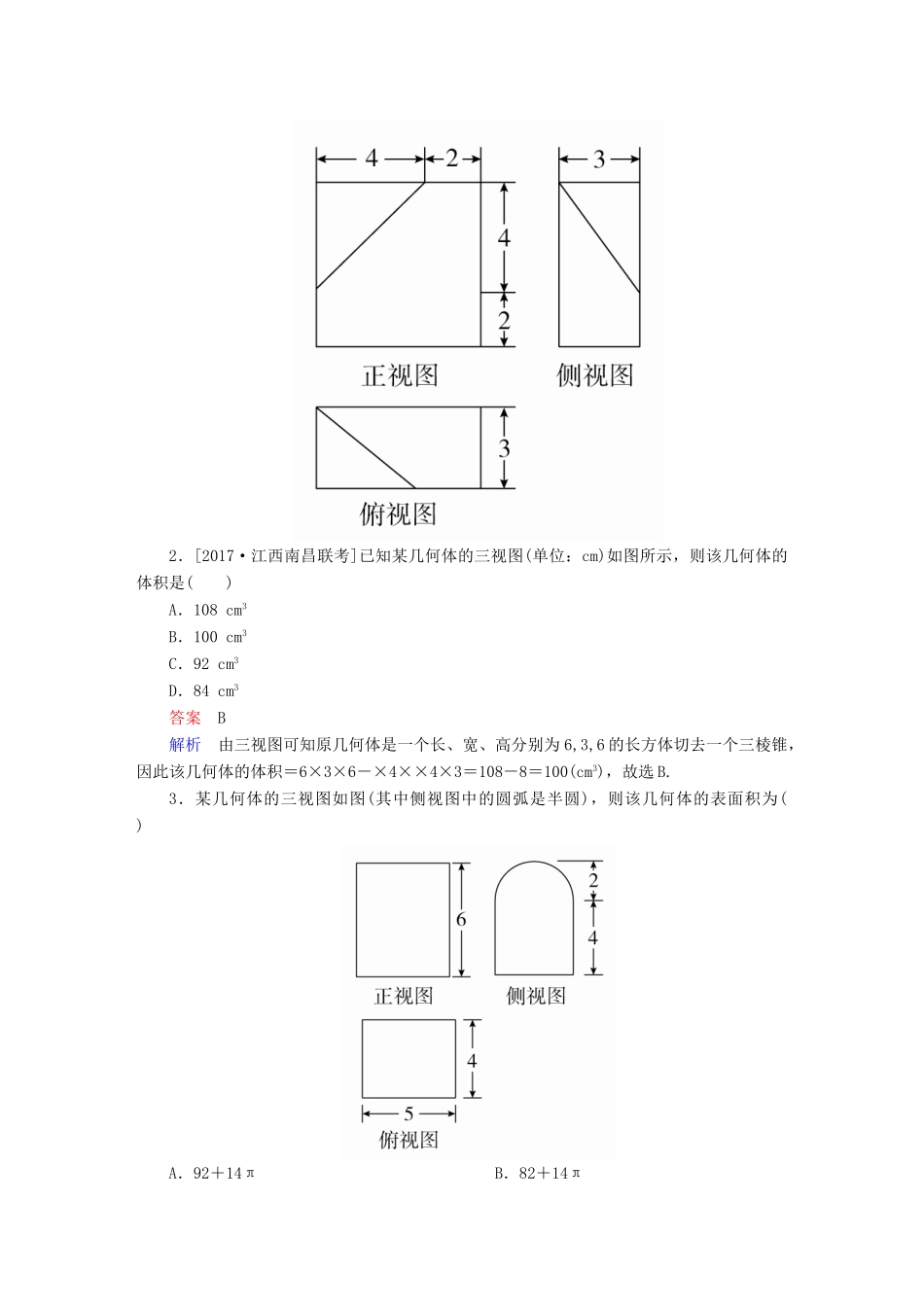
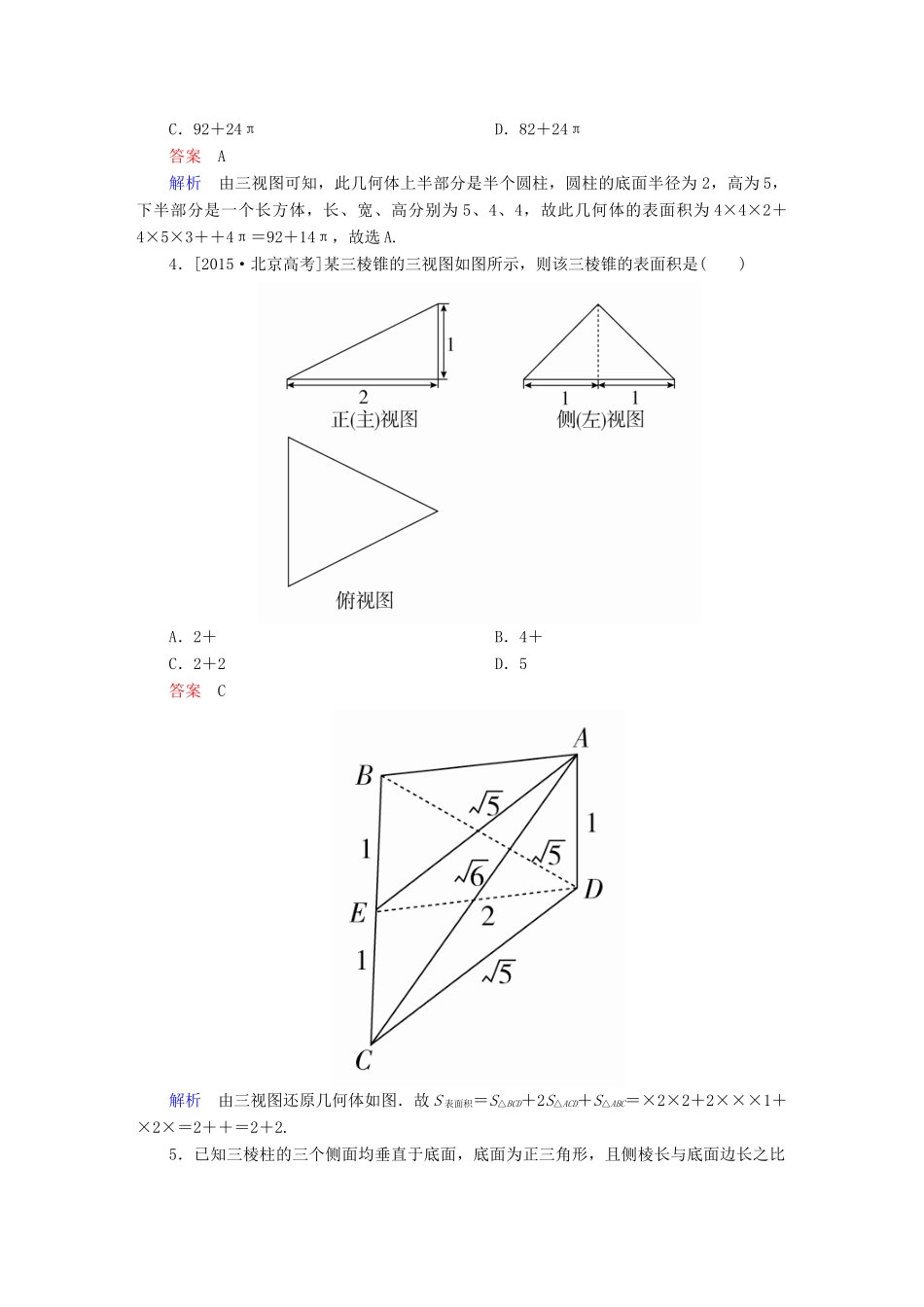
2018版高考数学一轮总复习第7章立体几何7.2空间几何体的表面积和体积模拟演练理[A级基础达标](时间:40分钟)1.[2016·全国卷Ⅰ]如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.20πD.28π答案A解析由三视图知该几何体为球去掉了所剩的几何体(如图),设球的半径为R,则×πR3=,故R=2,从而它的表面积S=×4πR2+×πR2=17π.故选A.2.[2017·江西南昌联考]已知某几何体的三视图(单位:cm)如图所示,则该几何体的体积是()A.108cm3B.100cm3C.92cm3D.84cm3答案B解析由三视图可知原几何体是一个长、宽、高分别为6,3,6的长方体切去一个三棱锥,因此该几何体的体积=6×3×6-×4××4×3=108-8=100(cm3),故选B.3.某几何体的三视图如图(其中侧视图中的圆弧是半圆),则该几何体的表面积为()A.92+14πB.82+14πC.92+24πD.82+24π答案A解析由三视图可知,此几何体上半部分是半个圆柱,圆柱的底面半径为2,高为5,下半部分是一个长方体,长、宽、高分别为5、4、4,故此几何体的表面积为4×4×2+4×5×3++4π=92+14π,故选A.4.[2015·北京高考]某三棱锥的三视图如图所示,则该三棱锥的表面积是()A.2+B.4+C.2+2D.5答案C解析由三视图还原几何体如图.故S表面积=S△BCD+2S△ACD+S△ABC=×2×2+2×××1+×2×=2++=2+2.5.已知三棱柱的三个侧面均垂直于底面,底面为正三角形,且侧棱长与底面边长之比为2∶1,顶点都在一个球面上,若该球的表面积为,则此三棱柱的侧面积为()A.B.C.8D.6答案D解析如图,根据球的表面积可得球的半径为r=,设三棱柱的底面边长为x,则2=x2+2,解得x=1,故该三棱柱的侧面积为3×1×2=6.6.[2016·天津高考]已知一个四棱锥的底面是平行四边形,该四棱锥的三视图如图所示(单位:m),则该四棱锥的体积为________m3.答案2解析四棱锥的底面是平行四边形,由三视图可知其底面积为2×1=2(m2),四棱锥的高为3m,所以四棱锥的体积V=×2×3=2(m3).7.[2017·江苏模拟]某几何体的三视图如图所示,其中正视图是腰长为2的等腰三角形,侧视图是半径为1的半圆,则该几何体的表面积是________.答案2(π+)解析由三视图可知此几何体的表面积分为两部分:底面积即俯视图的面积为2;侧面积为一个完整的圆锥的侧面积,且圆锥的母线长为2,底面半径为1,所以侧面积为2π.两部分加起来即为几何体的表面积,为2(π+).8.[2016·浙江高考]某几何体的三视图如图所示(单位:cm),则该几何体的表面积是________cm2,体积是________cm3.答案7232解析由几何体的三视图可得该几何体的直观图如图所示.该几何体由两个完全相同的长方体组合而成,其中AB=BC=2cm,BD=4cm,∴该几何体的体积V=2×2×4×2=32(cm3),表面积S=(2×2×3+2×4×3)×2=36×2=72(cm2).9.[2016·南宁二模]一个空间几何体的三视图如图所示,求该几何体的外接球的表面积.解依题意,题中的几何体是三棱锥A-BCD,如图所示.其中底面△BCD是等腰直角三角形,BC=CD=,AB⊥平面BCD,BC⊥CD,AB=,BD=2,AC⊥CD.取AD的中点M,连接BM,CM,则有BM=CM=AD==,该几何体的外接球的半径是,该几何体的外接球的表面积为4π×2=6π.10.如图,△ABC中,AB=8,BC=10,AC=6,DB⊥平面ABC,且AE∥FC∥BD,BD=3,FC=4,AE=5.求此几何体的体积.解解法一:如图,取CM=AN=BD,连接DM,MN,DN,用“分割法”把原几何体分割成一个直三棱柱和一个四棱锥.所以V几何体=V三棱柱+V四棱锥.由题知三棱柱ABC-NDM的体积为V1=×8×6×3=72.四棱锥D-MNEF的体积为:V2=×S梯形MNEF×DN=××(1+2)×6×8=24,则几何体的体积为:V=V1+V2=72+24=96.解法二:用“补形法”把原几何体补成一个直三棱柱,使AA′=BB′=CC′=8,所以V几何体=V三棱柱=×S△ABC×AA′=×24×8=96.[B级知能提升](时间:20分钟)11.[2016·全国卷Ⅲ]如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36B.54+18C.90D.81答案B解析由三视图可...