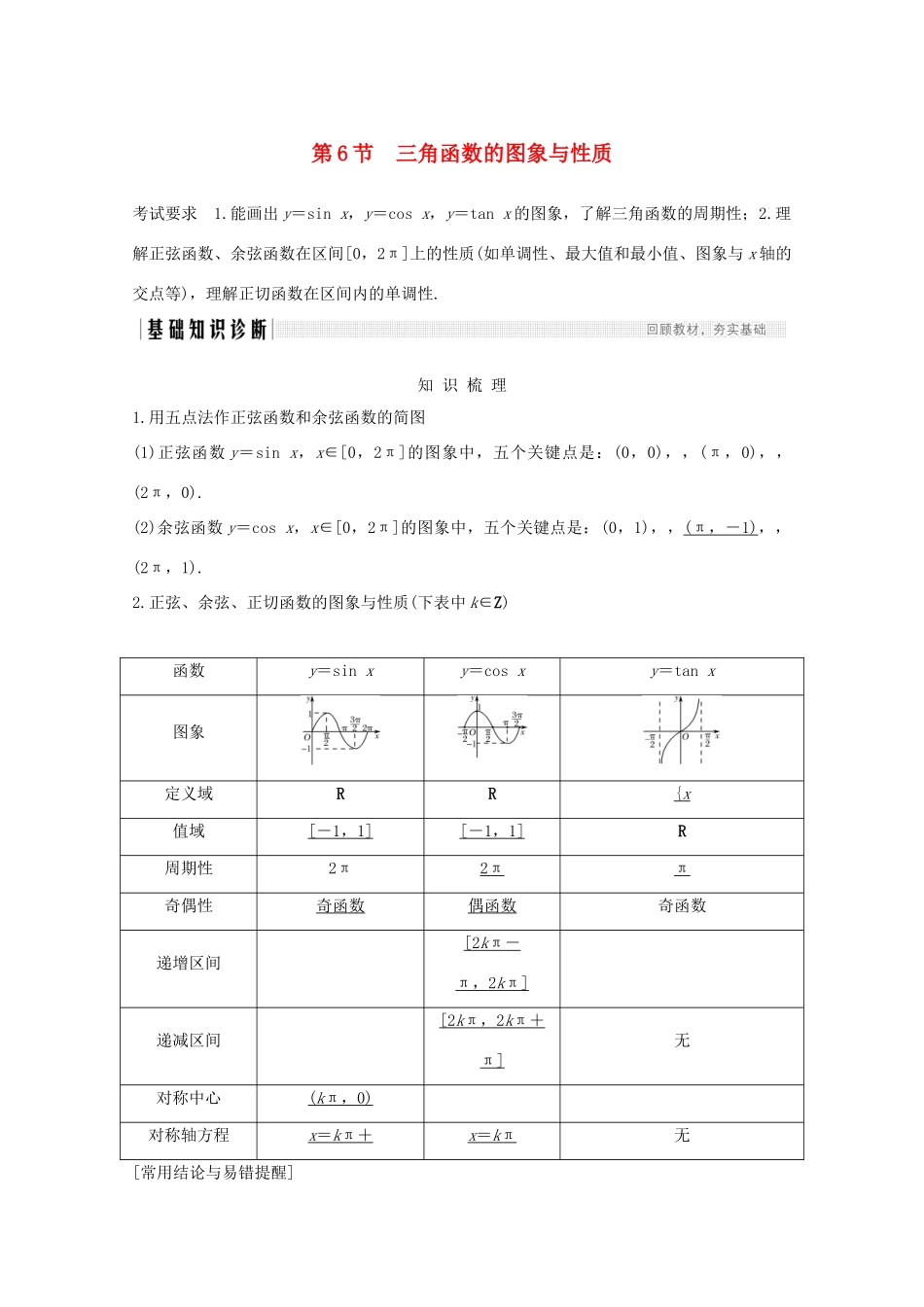
第6节三角函数的图象与性质考试要求1.能画出y=sinx,y=cosx,y=tanx的图象,了解三角函数的周期性;2.理解正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最大值和最小值、图象与x轴的交点等),理解正切函数在区间内的单调性.知识梳理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y=sinx,x∈[0,2π]的图象中,五个关键点是:(0,0),,(π,0),,(2π,0).(2)余弦函数y=cosx,x∈[0,2π]的图象中,五个关键点是:(0,1),,(π,-1),,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k∈Z)函数y=sinxy=cosxy=tanx图象定义域RR{x值域[-1,1][-1,1]R周期性2π2ππ奇偶性奇函数偶函数奇函数递增区间[2kπ-π,2kπ]递减区间[2kπ,2kπ+π]无对称中心(kπ,0)对称轴方程x=kπ+x=kπ无[常用结论与易错提醒]1.要注意求函数y=Asin(ωx+φ)的单调区间时A和ω的符号,尽量化成ω>0时情况,避免出现增减区间的混淆.2.正弦曲线、余弦曲线相邻两对称中心、相邻两对称轴之间的距离是半周期,相邻的对称中心与对称轴之间的距离是周期.而正切曲线相邻两对称中心之间的距离是半周期.3.三角函数中奇函数一般可化为y=Asinωx或y=Atanωx的形式,而偶函数一般可化为y=Acosωx+b的形式.诊断自测1.判断下列说法的正误.(1)由sin=sin知,是正弦函数y=sinx(x∈R)的一个周期.()(2)余弦函数y=cosx的对称轴是y轴.()(3)正切函数y=tanx在定义域内是增函数.()(4)已知y=ksinx+1,x∈R,则y的最大值为k+1.()(5)y=sin|x|是偶函数.()解析(1)函数y=sinx的周期是2kπ(k∈Z).(2)余弦函数y=cosx的对称轴有无穷多条,y轴只是其中的一条.(3)正切函数y=tanx在每一个区间(k∈Z)上都是增函数,但在定义域内不是单调函数,故不是增函数.(4)当k>0时,ymax=k+1;当k<0时,ymax=-k+1.答案(1)×(2)×(3)×(4)×(5)√2.关于周期函数,下列说法错误的是()A.函数f(x)=sin不是周期函数B.函数f(x)=sin不是周期函数C.函数f(x)=sin|x|不是周期函数D.函数f(x)=|sinx|+|cosx|的最小正周期为π解析f(x)=|sinx|+|cosx|的最小正周期为.答案D3.(2018·全国Ⅰ卷)已知函数f(x)=2cos2x-sin2x+2,则()A.f(x)的最小正周期为π,最大值为3B.f(x)的最小正周期为π,最大值为4C.f(x)的最小正周期为2π,最大值为3D.f(x)的最小正周期为2π,最大值为4解析易知f(x)=2cos2x-sin2x+2=3cos2x+1=3+1=cos2x+,则f(x)的最小正周期为π,当x=kπ(k∈Z)时,f(x)取得最大值,最大值为4.故选B.答案B4.若函数f(x)=sin(φ∈[0,2π])是偶函数,则φ=()A.B.C.D.解析由已知f(x)=sin是偶函数,可得=kπ+(k∈Z),即φ=3kπ+(k∈Z),又φ∈[0,2π],所以φ=.答案C5.(必修4P47B2改编)函数y=-tan的单调递减区间为________.解析因为y=tanx的单调递增区间为(k∈Z),所以由-+kπ<2x-<+kπ(k∈Z),得+<x<+(k∈Z),所以y=-tan的单调递减区间为(k∈Z).答案(k∈Z)6.设函数f(x)=2sin(ω>0,x∈R),最小正周期T=π,则实数ω=________,函数f(x)的图象的对称中心为________.解析由T==π,∴ω=2,f(x)=2sin,令2sin=0,得2x+=kπ(k∈Z),∴x=-(k∈Z),对称中心为(k∈Z).答案2(k∈Z)考点一三角函数的定义域及三角不等式【例1】(1)函数f(x)=-2tan的定义域是()A.B.C.D.(2)不等式+2cosx≥0的解集是________.(3)函数f(x)=+log2(2sinx-1)的定义域是________.解析(1)由正切函数的定义域得2x+≠kπ+(k∈Z),即x≠+(k∈Z),故选D.(2)由+2cosx≥0,得cosx≥-,由余弦函数的图象,得在一个周期[-π,π]上,不等式cosx≥-的解集为,故原不等式的解集为.(3)由题意得由①得-8≤x≤8,由②得sinx>,由正弦曲线得+2kπ