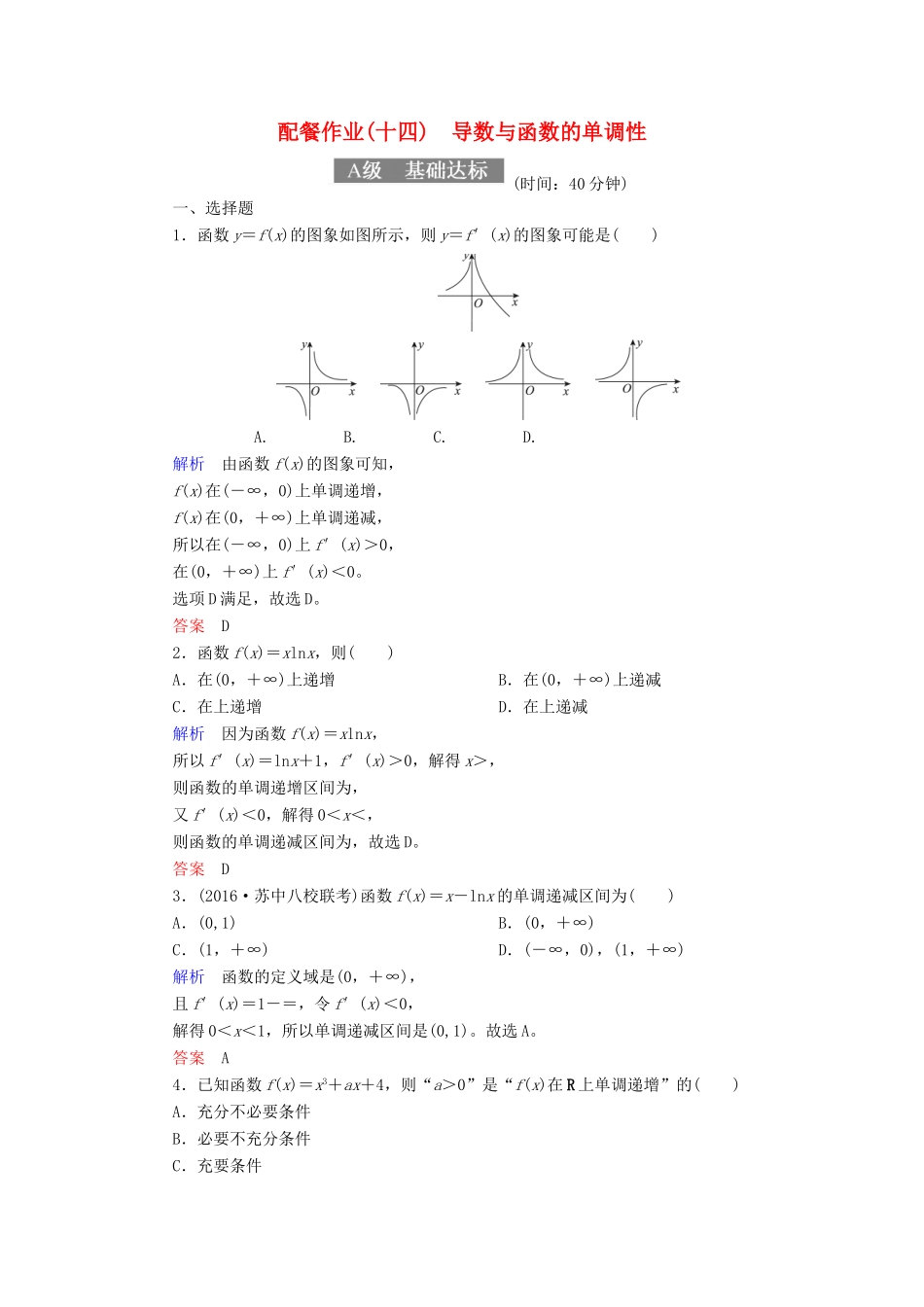
配餐作业(十四)导数与函数的单调性(时间:40分钟)一、选择题1.函数y=f(x)的图象如图所示,则y=f′(x)的图象可能是()A.B.C.D.解析由函数f(x)的图象可知,f(x)在(-∞,0)上单调递增,f(x)在(0,+∞)上单调递减,所以在(-∞,0)上f′(x)>0,在(0,+∞)上f′(x)<0。选项D满足,故选D。答案D2.函数f(x)=xlnx,则()A.在(0,+∞)上递增B.在(0,+∞)上递减C.在上递增D.在上递减解析因为函数f(x)=xlnx,所以f′(x)=lnx+1,f′(x)>0,解得x>,则函数的单调递增区间为,又f′(x)<0,解得0<x<,则函数的单调递减区间为,故选D。答案D3.(2016·苏中八校联考)函数f(x)=x-lnx的单调递减区间为()A.(0,1)B.(0,+∞)C.(1,+∞)D.(-∞,0),(1,+∞)解析函数的定义域是(0,+∞),且f′(x)=1-=,令f′(x)<0,解得0<x<1,所以单调递减区间是(0,1)。故选A。答案A4.已知函数f(x)=x3+ax+4,则“a>0”是“f(x)在R上单调递增”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件解析f′(x)=x2+a,当a≥0时,f′(x)≥0恒成立,故“a>0”是“f(x)在R上单调递增”的充分不必要条件。故选A。答案A5.若函数y=a(x3-x)的递减区间为,则a的取值范围是()A.a>0B.-1
1D.00。故选A。答案A6.(2017·湛江模拟)若函数f(x)=x+(b∈R)的导函数在区间(1,2)上有零点,则f(x)在下列区间上单调递增的是()A.(-2,0)B.(0,1)C.(1,+∞)D.(-∞,-2)解析由题意知,f′(x)=1-, 函数f(x)=x+(b∈R)的导函数在区间(1,2)上有零点,∴当1-=0时,b=x2,又x∈(1,2),∴b∈(1,4),令f′(x)>0,解得x<-或x>,即f(x)的单调递增区间为(-∞,-),(,+∞), b∈(1,4),∴(-∞,-2)符合题意,故选D。答案D7.已知函数f(x)的图象如图所示,则f(x)的解析式可能是()A.f(x)=-x3B.f(x)=+x3C.f(x)=-x3D.f(x)=--x3解析根据函数的定义域可以排除选项C,D,对于选项B:f′(x)=+3x2,当x>时f′(x)不可能恒小于0,即函数不可能恒为减函数,故不符合。故选A。答案A二、填空题8.函数f(x)=的单调递增区间是________。解析由导函数f′(x)==>0,得cosx>-,所以2kπ-0)。(1)若函数f(x)的单调递减区间是(0,4),则实数k的值为________;(2)若函数f(x)在(0,4)上为减函数,则实数k的取值范围是________。解析(1)f′(x)=3kx2+6(k-1)x,由题意知f′(4)=0,解得k=。(2)由f′(x)=3kx2+6(k-1)x≤0并结合导函数的图象可知,必有-≥4,解得k≤。又k>0,故0