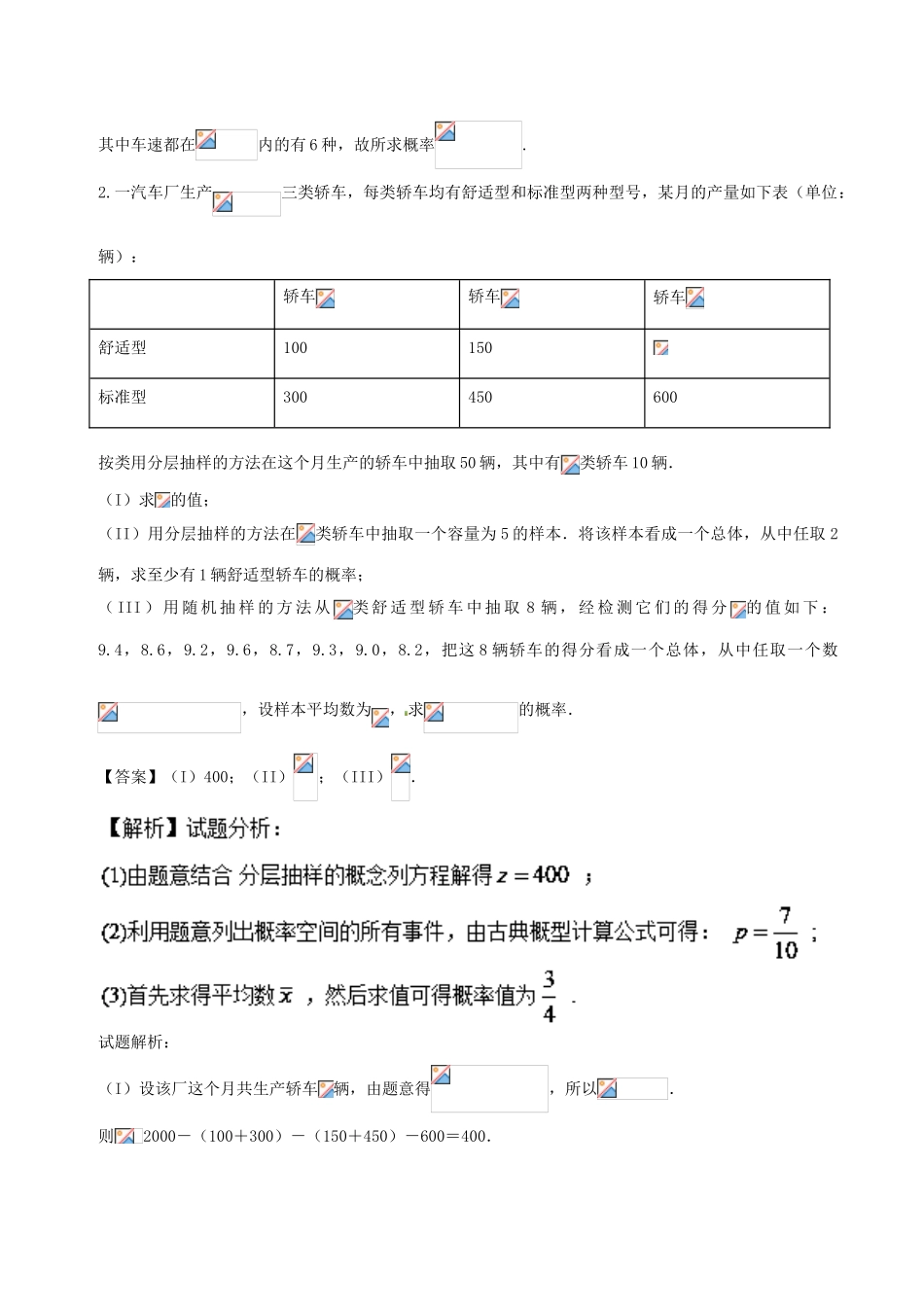
命题角度3.2随机事件的频率与概率1.随机抽取了40辆汽车在经过路段上某点时的车速(km/h),现将其分成六段:,,,,,,后得到如图所示的频率分布直方图.(Ⅰ)现有某汽车途经该点,则其速度低于80km/h的概率约是多少?(Ⅱ)根据直方图可知,抽取的40辆汽车经过该点的平均速度约是多少?(Ⅲ)在抽取的40辆且速度在(km/h)内的汽车中任取2辆,求这2辆车车速都在(km/h)内的概率.【答案】(I);(II)(km/h);(III).试题解析:(Ⅰ)速度低于80km/h的概率约为:.(Ⅱ)这40辆小型车辆的平均车速为:(km/h),(Ⅲ)车速在内的有2辆,记为车速在内的有4辆,记为,从中抽2辆,抽法为共15种,其中车速都在内的有6种,故所求概率.2.一汽车厂生产三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):轿车轿车轿车舒适型100150标准型300450600按类用分层抽样的方法在这个月生产的轿车中抽取50辆,其中有类轿车10辆.(I)求的值;(II)用分层抽样的方法在类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;(III)用随机抽样的方法从类舒适型轿车中抽取8辆,经检测它们的得分的值如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2,把这8辆轿车的得分看成一个总体,从中任取一个数,设样本平均数为,求的概率.【答案】(I)400;(II);(III).试题解析:(I)设该厂这个月共生产轿车辆,由题意得,所以.则2000-(100+300)-(150+450)-600=400.(II)设所抽样本中有辆舒适型轿车,由题意,得.因此抽取的容量为5的样本中,有2辆舒适型轿车,3辆标准型轿车.用表示2辆舒适型轿车,用表示3辆标准型轿车,用表示事件“在该样本中任取2辆,其中至少有1辆舒适型轿车”,则基本事件空间包含的基本事件有:,,,,,,,,,,共10个.事件的基本事件有:,,,,,,,共7个.故,即所求概率为.3.已知某中学高三文科班学生的数学与地理的水平测试成绩抽样统计如下表:若抽取学生人,成绩分为(优秀),(良好),(及格)三个等次,设分别表示数学成绩与地理成绩,例如:表中地理成绩为等级的共有(人),数学成绩为等级且地理成绩为等级的共有8人.已知与均为等级的概率是.(1)设在该样本中,数学成绩的优秀率是,求的值;(2)已知,,求数学成绩为等级的人数比等级的人数多的概率.【答案】(1)(2)试题解析:(1),∴,故而所以(2)且由得则的所有可能结果为,,...共有18种,可能结果为,...共有8种,则所求.点睛:古典概型中基本事件数的探求方法(1)列举法.(2)树状图法:适合于较为复杂的问题中的基本事件的探求.对于基本事件有“有序”与“无序”区别的题目,常采用树状图法.(3)列表法:适用于多元素基本事件的求解问题,通过列表把复杂的题目简单化、抽象的题目具体化.(4)排列组合法:适用于限制条件较多且元素数目较多的题目.4.某中学为了解高中入学新生的身高情况,从高一年级学生中按分层抽样共抽取了50名学生的身高数据,分组统计后得到了这50名学生身高的频数分布表:(Ⅰ)在答题卡上作出这50名学生身高的频率分布直方图;(Ⅱ)估计这50名学生身高的方差(同一组中的数据用该组区间的中点值作代表);(Ⅲ)现从身高在这6名学生中随机抽取3名,求至少抽到1名女生的概率.【答案】(Ⅰ)见解析;(Ⅱ)估计这50名学生身高的方差为80;(Ⅲ).试题解析:(Ⅰ)这50名学生身高的频率分布直方图如下图所示:(Ⅱ)由题意可估计这50名学生的平均身高为.所以估计这50名学生身高的方差为.所以估计这50名学生身高的方差为80.(Ⅱ)记身高在的4名男生为,,,,2名女生为,.从这6名学生中随机抽取3名学生的情况有:,,,,,,,,,,,,,,,,,,,共20个基本事件.其中至少抽到1名女生的情况有:,,,,,,,,,,,,,,,共16个基本事件.所以至少抽到1名女生的概率为(Ⅰ)这50名学生身高的频率分布直方图如下图所示:(Ⅲ)记身高在的4名男生为,,,,2名女生为,.从这6名学生中随机抽取3名学生的情况有:,,,,,,,,,,,,,,,,,,,共20个基本事件.其中至少抽到1名女生的情况有:,,,,,,,,,,,,,,,共16...