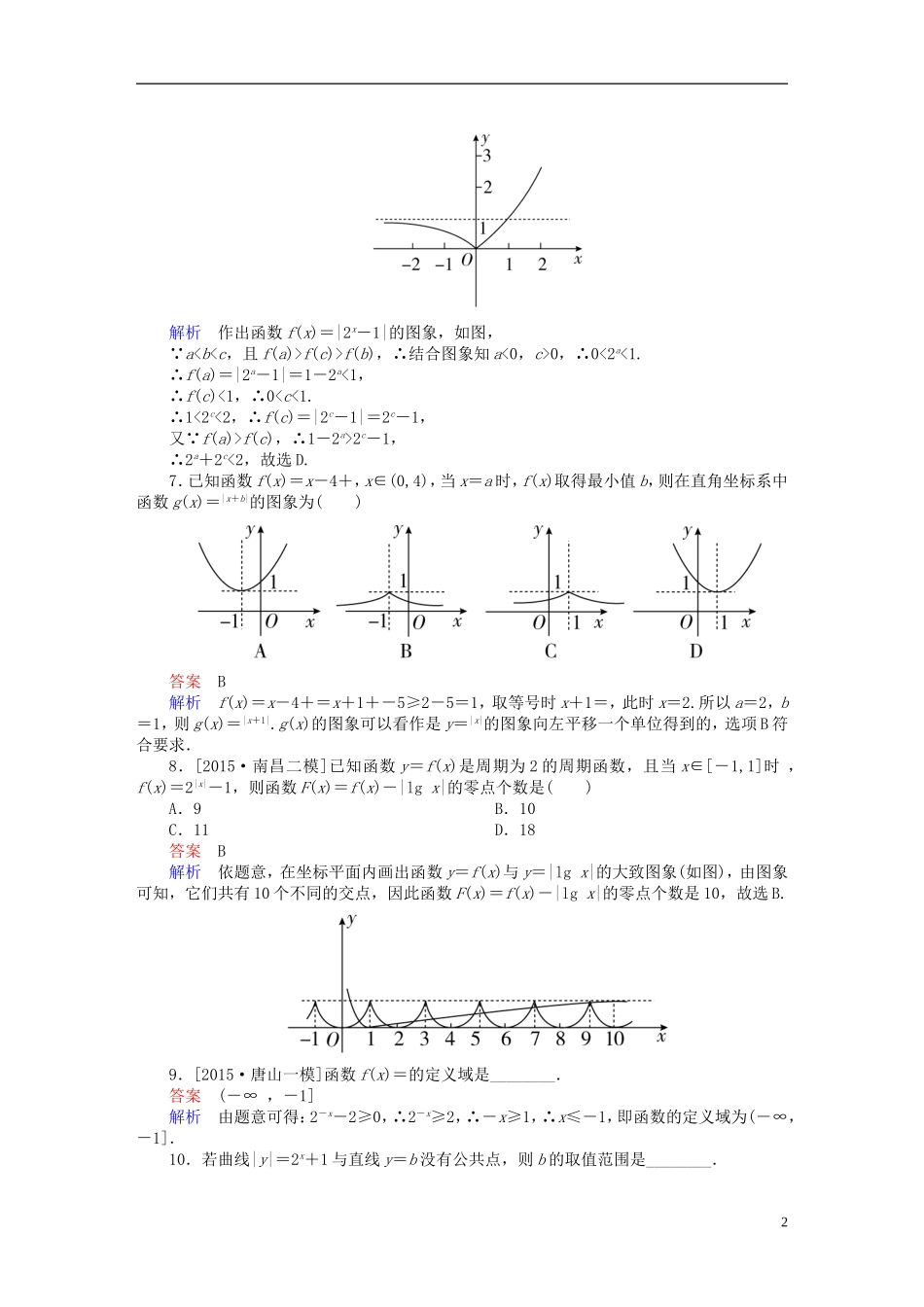
第二章函数、导数及其应用2.5指数与指数函数练习理[A组·基础达标练]1.化简[(-2)6]-(-1)0的结果为()A.-9B.7C.-10D.9答案B解析原式=(26)-1=7.2.[2015·吉林期中]函数y=4x+2x+1+1的值域为()A.(0,+∞)B.(1,+∞)C.[1,+∞)D.(-∞,+∞)答案B解析令2x=t,则函数y=4x+2x+1+1可化为y=t2+2t+1=(t+1)2(t>0). 函数y=(t+1)2在(0,+∞)上递增,∴y>1.∴所求值域为(1,+∞).故选B.3.[2016·西安八校联考]已知0
anB.bmnaD.mb1)在(0,+∞)上为单调递增函数,且0f(c)>f(b),则下列结论中,一定成立的是()A.a<0,b<0,c<0B.a<0,b≥0,c>0C.2-a<2cD.2a+2c<2答案D1解析作出函数f(x)=|2x-1|的图象,如图, af(c)>f(b),∴结合图象知a<0,c>0,∴0<2a<1.∴f(a)=|2a-1|=1-2a<1,∴f(c)<1,∴0f(c),∴1-2a>2c-1,∴2a+2c<2,故选D.7.已知函数f(x)=x-4+,x∈(0,4),当x=a时,f(x)取得最小值b,则在直角坐标系中函数g(x)=|x+b|的图象为()答案B解析f(x)=x-4+=x+1+-5≥2-5=1,取等号时x+1=,此时x=2.所以a=2,b=1,则g(x)=|x+1|.g(x)的图象可以看作是y=|x|的图象向左平移一个单位得到的,选项B符合要求.8.[2015·南昌二模]已知函数y=f(x)是周期为2的周期函数,且当x∈[-1,1]时,f(x)=2|x|-1,则函数F(x)=f(x)-|lgx|的零点个数是()A.9B.10C.11D.18答案B解析依题意,在坐标平面内画出函数y=f(x)与y=|lgx|的大致图象(如图),由图象可知,它们共有10个不同的交点,因此函数F(x)=f(x)-|lgx|的零点个数是10,故选B.9.[2015·唐山一模]函数f(x)=的定义域是________.答案(-∞,-1]解析由题意可得:2-x-2≥0,∴2-x≥2,∴-x≥1,∴x≤-1,即函数的定义域为(-∞,-1].10.若曲线|y|=2x+1与直线y=b没有公共点,则b的取值范围是________.2答案[-1,1]解析(数形结合法)曲线|y|=2x+1即为y=2x+1或y=-(2x+1),作出曲线的图象(如右图),要使该曲线与直线y=b没有公共点,则要求-1≤b≤1.11.[2016·皖南八校联考]对于给定的函数f(x)=ax-a-x(x∈R,a>0,a≠1),下面给出五个命题,其中真命题是________.(只需写出所有真命题的编号)①函数f(x)的图象关于原点对称;②函数f(x)在R上不具有单调性;③函数f(|x|)的图象关于y轴对称;④当01时,函数f(|x|)的最大值是0.答案①③④解析 f(-x)=-f(x),∴f(x)为奇函数,f(x)的图象关于原点对称,①真;当a>1时,f(x)在R上为增函数,当01时,f(x)在(-∞,0)上为减函数,在[0,+∞)上为增函数,∴当x=0时,y=f(x)的最小值为0,⑤假,综上,真命题是①③④.12.已知函数y=b+ax2+2x(a,b是常数且a>0,a≠1)在区间上有ymax=3,ymin=,试求a,b的值.解 x∈,∴t=x2+2x=(x+1)2-1,值域为[-1,0],即t∈[-1,0].(1)若a>1,函数y=at在[-1,0]上为增函数,∴at∈,则b+ax2+2x∈,依题...