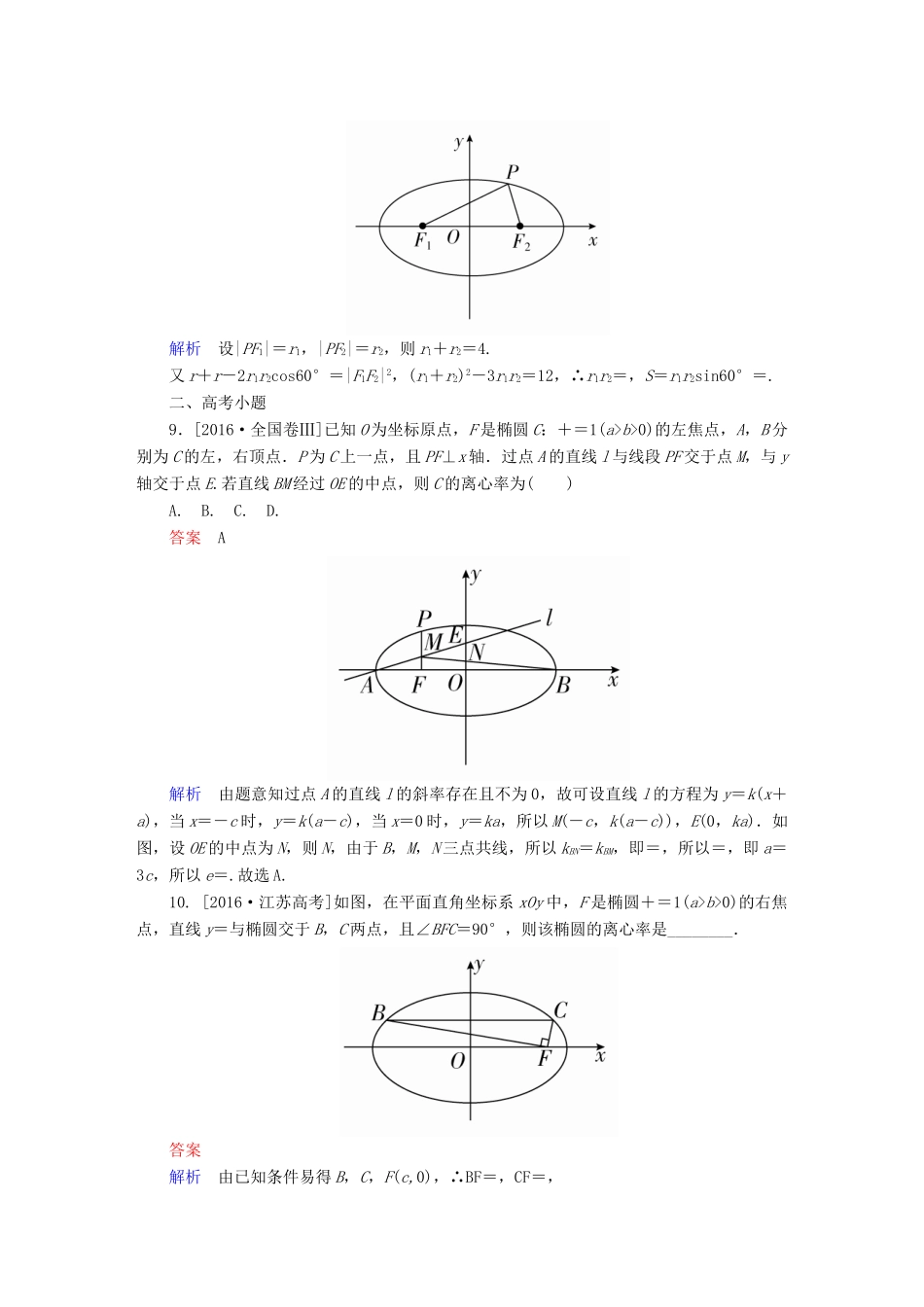
考点测试52椭圆一、基础小题1.中心在原点,焦点在x轴上,若长轴长为18,且两个焦点恰好将长轴三等分,则此椭圆的方程是()A.+=1B.+=1C.+=1D.+=1答案A解析依题意知:2a=18,∴a=9,2c=×2a,∴c=3,∴b2=a2-c2=81-9=72,∴椭圆方程为+=1.2.已知椭圆的方程为2x2+3y2=m(m>0),则此椭圆的离心率为()A.B.C.D.答案B解析2x2+3y2=m(m>0)⇒+=1,∴c2=-=.∴e2=,∴e=.故选B.3.椭圆x2+my2=1的焦点在y轴上,长轴长是短轴长的2倍,则m等于()A.B.2C.4D.答案D解析由x2+=1及题意知,2=2×2×1,m=,故选D.4.已知椭圆+y2=1的焦点为F1、F2,点M在该椭圆上,且MF1·MF2=0,则点M到y轴的距离为()A.B.C.D.答案B解析设M(x,y),由MF1·MF2=0,得x2+y2=c2=3,又+y2=1,解得x=±.5.已知圆(x+2)2+y2=36的圆心为M,设A为圆上任一点,且点N(2,0),线段AN的垂直平分线交MA于点P,则动点P的轨迹是()A.圆B.椭圆C.双曲线D.抛物线答案B解析点P在线段AN的垂直平分线上,故|PA|=|PN|,又AM是圆的半径,∴|PM|+|PN|=|PM|+|PA|=|AM|=6>|MN|,由椭圆定义知,P的轨迹是椭圆.6.设F1,F2是椭圆E:+=1(a>b>0)的左、右焦点,P为直线x=上一点,△F2PF1是底角为30°的等腰三角形,则E的离心率为()A.B.C.D.答案C解析令c=.如图,据题意,|F2P|=|F1F2|,∠F1PF2=30°,∴∠F1F2P=120°,∴∠PF2x=60°,∴|F2P|=2=3a-2c. |F1F2|=2c,∴3a-2c=2c,∴3a=4c,∴=,即椭圆的离心率为.故选C.7.已知点F1,F2是椭圆x2+2y2=2的两个焦点,点P是该椭圆上的一个动点,那么|PF1+PF2|的最小值是()A.0B.1C.2D.2答案C解析设P(x0,y0),则PF1=(-1-x0,-y0),PF2=(1-x0,-y0),∴PF1+PF2=(-2x0,-2y0),∴|PF1+PF2|==2=2. 点P在椭圆上,∴0≤y≤1,∴当y=1时,|PF1+PF2|取最小值2.故选C.8.已知P是椭圆+y2=1上的一点,F1、F2是椭圆的两个焦点,且∠F1PF2=60°,则△F1PF2的面积是________.答案解析设|PF1|=r1,|PF2|=r2,则r1+r2=4.又r+r-2r1r2cos60°=|F1F2|2,(r1+r2)2-3r1r2=12,∴r1r2=,S=r1r2sin60°=.二、高考小题9.[2016·全国卷Ⅲ]已知O为坐标原点,F是椭圆C:+=1(a>b>0)的左焦点,A,B分别为C的左,右顶点.P为C上一点,且PF⊥x轴.过点A的直线l与线段PF交于点M,与y轴交于点E.若直线BM经过OE的中点,则C的离心率为()A.B.C.D.答案A解析由题意知过点A的直线l的斜率存在且不为0,故可设直线l的方程为y=k(x+a),当x=-c时,y=k(a-c),当x=0时,y=ka,所以M(-c,k(a-c)),E(0,ka).如图,设OE的中点为N,则N,由于B,M,N三点共线,所以kBN=kBM,即=,所以=,即a=3c,所以e=.故选A.10.[2016·江苏高考]如图,在平面直角坐标系xOy中,F是椭圆+=1(a>b>0)的右焦点,直线y=与椭圆交于B,C两点,且∠BFC=90°,则该椭圆的离心率是________.答案解析由已知条件易得B,C,F(c,0),∴BF=,CF=,由∠BFC=90°,可得BF·CF=0,所以+2=0,c2-a2+b2=0,即4c2-3a2+(a2-c2)=0,亦即3c2=2a2,所以=,则e==.11.[2014·安徽高考]设F1,F2分别是椭圆E:x2+=1(00).又 |AF1|=3|F1B|,∴由AF1=3F1B,得B,代入x2+=1,得+=1,又c2=1-b2,∴b2=.故椭圆E的方程为x2+y2=1.12.[2014·江西高考]过点M(1,1)作斜率为-的直线与椭圆C:+=1(a>b>0)相交于A,B两点,若M是线段AB的中点,则椭圆C的离心率等于________.答案解析设A(x1,y1),B(x2,y2),则+=1,①+=1.②①、②两式相减并整理,得=-·.把已知条件代入上式,得-=-×,∴=,故椭圆的离心率e==.13.[2014·辽宁高考]已知椭圆C:+=1,点M与C的焦点不重合.若M关于C的焦点的对称点分别为A,B,线段MN的中点在C上,则|AN|+|BN|=________.答案12解析解法一:由椭圆方程知椭圆C的左焦点为F1(-,0),右焦点...