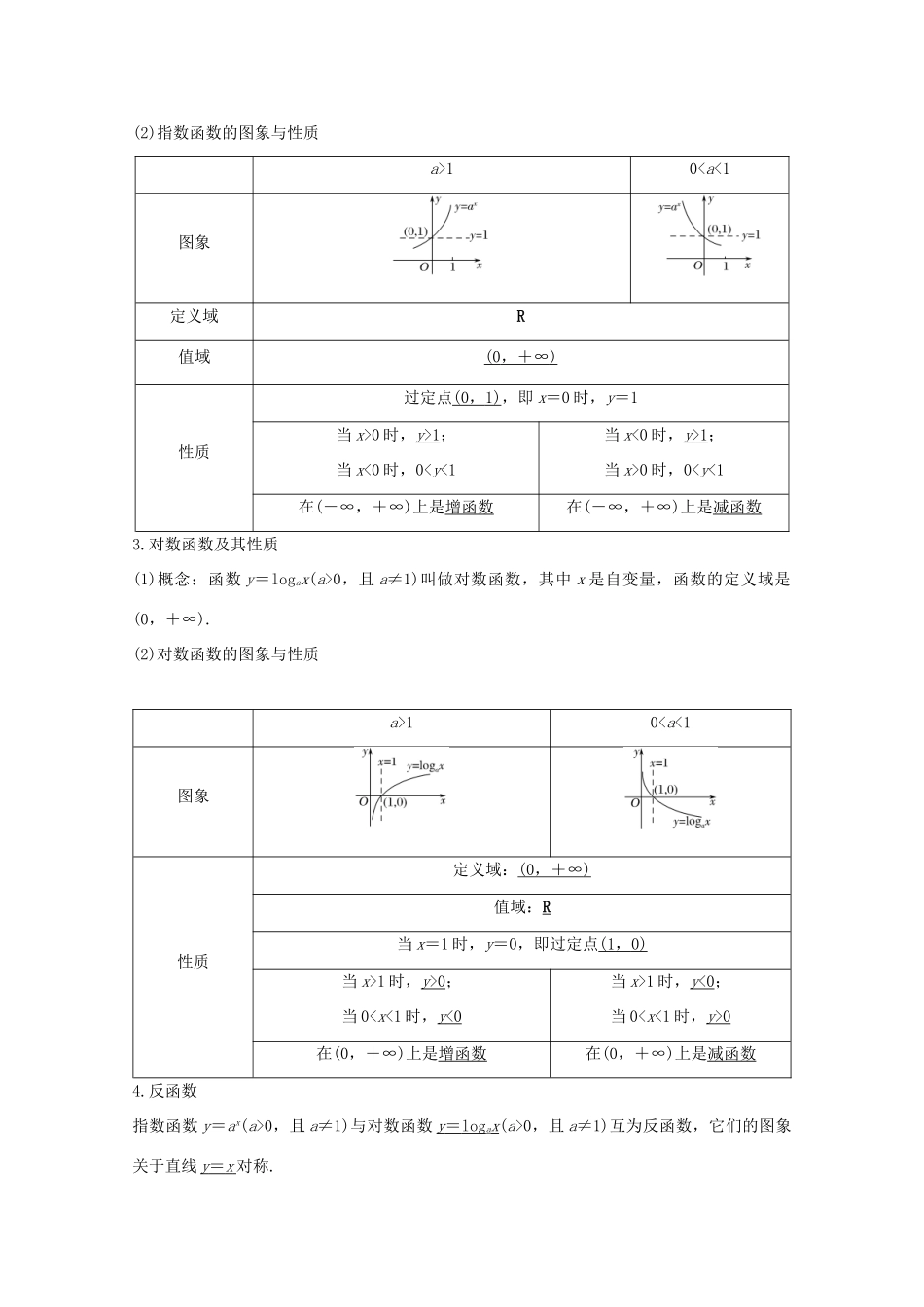
第6节幂函数、指数函数、对数函数考试要求1.了解幂函数的概念,掌握幂函数y=x,y=x2,y=x3,y=,y=x的图象和性质;2.理解指数函数的概念,掌握指数函数的图象、性质及应用;3.理解对数函数的概念,掌握对数函数的图象、性质及应用.知识梳理1.幂函数(1)幂函数的定义一般地,形如y=xα的函数称为幂函数,其中x是自变量,α为常数.(2)常见的5种幂函数的图象(3)常见的5种幂函数的性质2.指数函数及其性质(1)概念:函数y=ax(a>0且a≠1)叫做指数函数,其中指数x是自变量,函数的定义域是R,a是底数.(2)指数函数的图象与性质a>10
0时,y>1;当x<0时,01;当x>0时,00,且a≠1)叫做对数函数,其中x是自变量,函数的定义域是(0,+∞).(2)对数函数的图象与性质a>101时,y>0;当01时,y<0;当00在(0,+∞)上是增函数在(0,+∞)上是减函数4.反函数指数函数y=ax(a>0,且a≠1)与对数函数y=logax(a>0,且a≠1)互为反函数,它们的图象关于直线y=x对称.[常用结论与易错提醒]1.幂函数满足三个条件:(1)幂底是单自变量;(2)指数为常数;(3)系数为1.类似地指数函数、对数函数也分别满足三个条件.2.(1)幂函数图象的分布规律:作一直线x=t>1,与幂函数交点在上面的幂函数的指数大;(2)指数函数图象的分布规律:作一直线x=t>0,与指数函数交点在上面的指数函数的底数大;(3)对数函数图象的分布规律:作一直线y=k>0,与对数函数交点在右边的对数函数的底数大.诊断自测1.判断下列说法的正误.(1)幂函数y=x0与常值函数y=1图象相同.()(2)函数y=2x是幂函数.()(3)y=2x-1是指数函数,y=loga(x2+1)(a>0,且a≠1)是对数函数.()(4)函数y=ln与y=ln(x+1)-ln(x-1)的定义域相同.()解析(1)错误,y=1的图象去掉点(0,1)才是y=x0的图象;(2)错误,因为x的系数不是1;(3)错误,y=2x-1=·2x,2x前面的系数不为1,y=loga(x2+1)(a>0且a≠1),真数为x2+1而不是单自变量x.(4)错误,y=ln的定义域为(-∞,-1)∪(1,+∞),而y=ln(x+1)-ln(x-1)的定义域为(1,+∞),故函数的定义域不同.答案(1)×(2)×(3)×(4)×2.(2019·浙江卷)在同一直角坐标系中,函数y=,y=loga(a>0,且a≠1)的图象可能是()解析当01时,函数y=ax的图象过定点(0,1),在R上单调递增,于是函数y=的图象过定点(0,1),在R上单调递减,函数y=loga的图象过定点,在上单调递增.显然A,B,C,D四个选项都不符合.故选D.答案D3.(一题多解)已知函数y=loga(x+c)(a,c为常数,其中a>0,且a≠1)的图象如图,则下列结论成立的是()A.a>1,c>1B.a>1,01D.00,即logac>0,所以00,且a≠1时,函数f(x)=ax-3-2必过定点________,其值域为________.解析函数f(x)=ax-3-2的图象是将函数y=ax的图象向右平移3个单位,再向下平移2个单位得到的.故函数f(x)=ax-3-2必过定点(3,-1),其值域为(-2,+∞).答案(3,-1)(-2,+∞)考点一幂函数【例1】(1)(2018·上海卷)已知α∈.若幂函数...