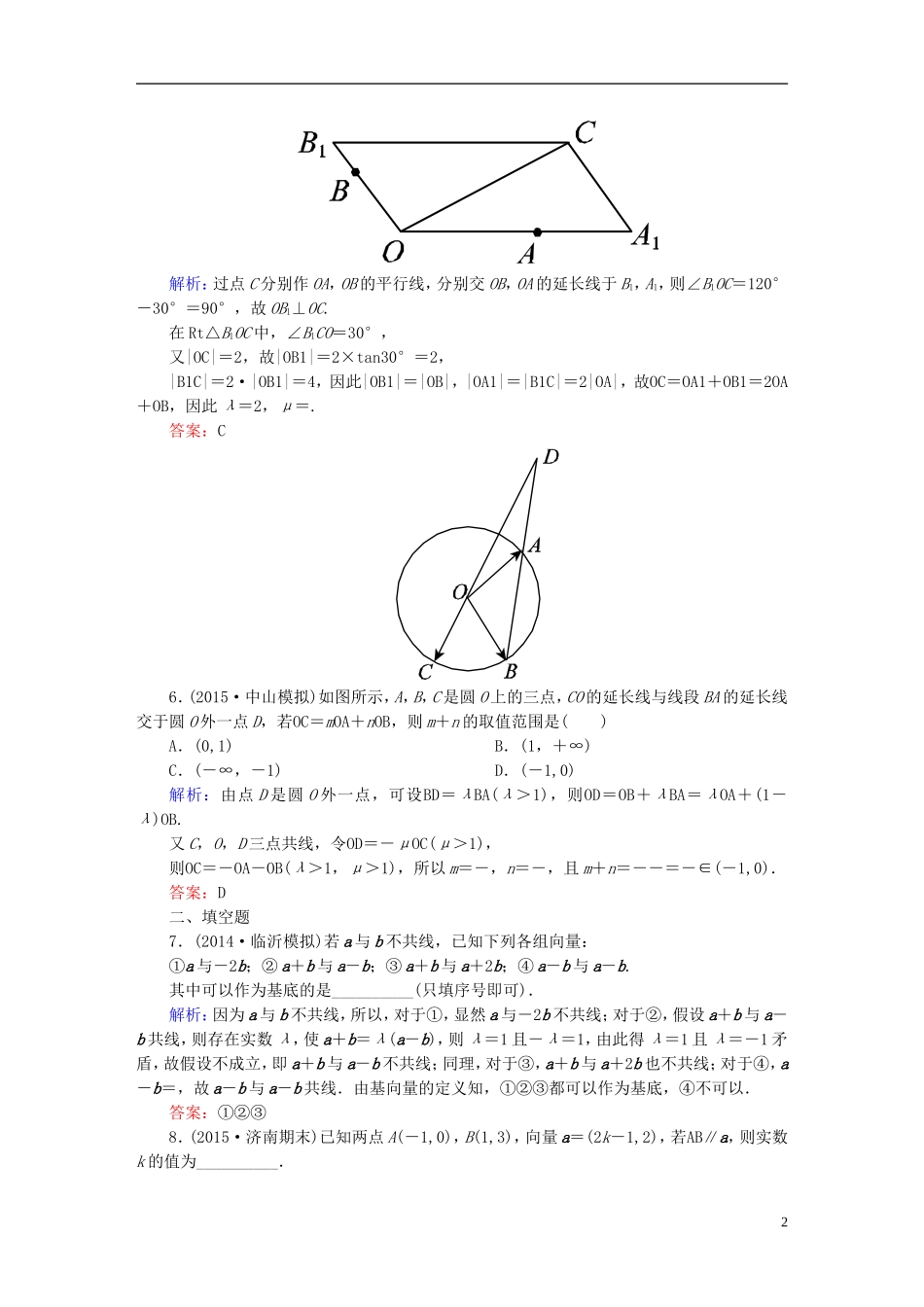
课时作业24平面向量基本定理及坐标表示一、选择题1.(2014·宜昌模拟)若向量a=(1,1),b=(-1,1),c=(4,2),则c=()A.3a+bB.3a-bC.-a+3bD.a+3b解析:设c=xa+yb,则所以故c=3a-b.答案:B2.(2014·郑州模拟)已知向量OA=(k,12),OB=(4,5),OC=(-k,10),且A,B,C三点共线,则k的值是()A.-B.C.D.解析:AB=OB-OA=(4-k,-7),AC=OC-OA=(-2k,-2).因为A,B,C三点共线,所以AB,AC共线,所以-2×(4-k)=-7×(-2k),解得k=-.答案:A3.(2015·大庆模拟)已知向量a=(1-sinθ,1),b=,若a∥b,则锐角θ等于()A.30°B.45°C.60°D.75°解析:由a∥b得,(1-sinθ)(1+sinθ)-1×=0,解得sinθ=±.又θ为锐角,所以θ=45°.答案:B4.(2014·石家庄模拟)已知向量OA=(1,3),OB=(3,-1),且AP=2PB,则点P的坐标为()A.(2,-4)B.C.D.(-2,4)解析:设点P的坐标为(x,y),由AP=2PB可得(x-1,y-3)=2(3-x,-1-y),故有x-1=6-2x,且y-3=-2-2y,解得x=,y=,故点P的坐标为.答案:C5.(2015·三明模拟)如图,平面内有三个向量OA,OB,OC,其中OA与OB的夹角为120°,OA与OC的夹角为30°,且|OA|=2,|OB|=,|OC|=2,若OC=λOA+μOB(λ,μ∈R),则()A.λ=4,μ=2B.λ=,μ=C.λ=2,μ=D.λ=,μ=1解析:过点C分别作OA,OB的平行线,分别交OB,OA的延长线于B1,A1,则∠B1OC=120°-30°=90°,故OB1⊥OC.在Rt△B1OC中,∠B1CO=30°,又|OC|=2,故|OB1|=2×tan30°=2,|B1C|=2·|OB1|=4,因此|OB1|=|OB|,|OA1|=|B1C|=2|OA|,故OC=OA1+OB1=2OA+OB,因此λ=2,μ=.答案:C6.(2015·中山模拟)如图所示,A,B,C是圆O上的三点,CO的延长线与线段BA的延长线交于圆O外一点D,若OC=mOA+nOB,则m+n的取值范围是()A.(0,1)B.(1,+∞)C.(-∞,-1)D.(-1,0)解析:由点D是圆O外一点,可设BD=λBA(λ>1),则OD=OB+λBA=λOA+(1-λ)OB.又C,O,D三点共线,令OD=-μOC(μ>1),则OC=-OA-OB(λ>1,μ>1),所以m=-,n=-,且m+n=--=-∈(-1,0).答案:D二、填空题7.(2014·临沂模拟)若a与b不共线,已知下列各组向量:①a与-2b;②a+b与a-b;③a+b与a+2b;④a-b与a-b.其中可以作为基底的是__________(只填序号即可).解析:因为a与b不共线,所以,对于①,显然a与-2b不共线;对于②,假设a+b与a-b共线,则存在实数λ,使a+b=λ(a-b),则λ=1且-λ=1,由此得λ=1且λ=-1矛盾,故假设不成立,即a+b与a-b不共线;同理,对于③,a+b与a+2b也不共线;对于④,a-b=,故a-b与a-b共线.由基向量的定义知,①②③都可以作为基底,④不可以.答案:①②③8.(2015·济南期末)已知两点A(-1,0),B(1,3),向量a=(2k-1,2),若AB∥a,则实数k的值为__________.2解析:因为A(-1,0),B(1,3),所以AB=(2,3).又因为AB∥a,所以=,故k=.答案:9.(2015·南京质检)设OA=(1,-2),OB=(a,-1),OC=(-b,0),a>0,b>0,O为坐标原点,若A,B,C三点共线,则+的最小值是________.解析:AB=OB-OA=(a-1,1),AC=OC-OA=(-b-1,2). A、B、C三点共线,∴AB∥AC.∴=.∴2a+b=1.∴+=+=4++≥4+2=8,当且仅当=时取等号.∴+的最小值是8.答案:8三、解答题10.(2015·郑州月考)如图,已知△OCB中,A是CB的中点,D是将OB分成2∶1的一个内分点,DC和OA交于点E,设OA=a,OB=b.(1)用a和b表示向量OC,DC;(2)若OE=λOA,求实数λ的值.解析:(1)由题意知,A是BC的中点,且OD=OB,由平行四边形法则,得OB+OC=2OA,所以OC=2OA-OB=2a-b,DC=OC-OD=(2a-b)-b=2a-b.(2)由题意知,EC∥DC,故设EC=xDC.因为EC=OC-OE=(2a-b)-λa=(2-λ)a-b,DC=2a-b,所以(2-λ)a-b=x.因为a与b不共线,由平面向量基本定理,得解得故λ=.11.(2014·陕西卷)在直角坐标系xOy中,已知点A(1,1),B(2,3),C(3,2),点P(x,y)在△ABC三边围成的区域(含边界)上,且OP=mAB+nAC(m,n∈R).(1)若m=n=,求|OP|;(2)用x,y表示m-n,并求m-n的最大值...