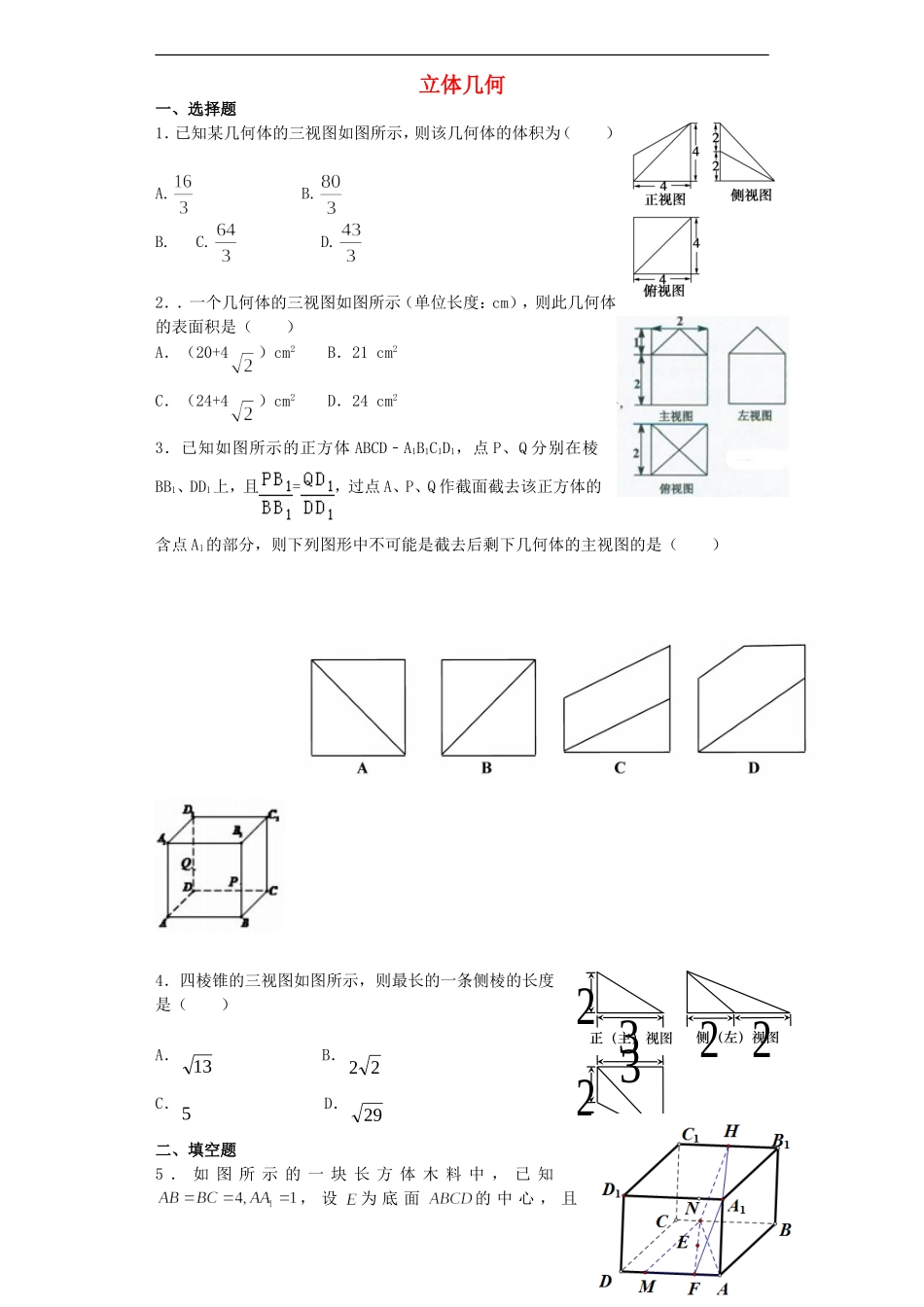
立体几何一、选择题1.已知某几何体的三视图如图所示,则该几何体的体积为()A.B.B.C.D.2..一个几何体的三视图如图所示(单位长度:cm),则此几何体的表面积是()A.(20+4)cm2B.21cm2C.(24+4)cm2D.24cm23.已知如图所示的正方体ABCD﹣A1B1C1D1,点P、Q分别在棱BB1、DD1上,且=,过点A、P、Q作截面截去该正方体的含点A1的部分,则下列图形中不可能是截去后剩下几何体的主视图的是()4.四棱锥的三视图如图所示,则最长的一条侧棱的长度是()A.13B.22C.5D.29二、填空题5.如图所示的一块长方体木料中,已知,设为底面的中心,且1正(主)视图侧(左)视图俯视图322232,则该长方体中经过点的截面面积的最小值为.6.长方体中,已知,,棱在平面内,则长方体在平面内的射影所构成的图形面积的取7.如右图,正方体的棱长为1,P值范围是.为BC的中点,Q为线段上的动点,过点A,P,Q的平面截该正方体所得的截面记为S.则下列命题正确的是_____(写出所有正确命题的编号).①当时,S为四边形;②当时,S不为等腰梯形;③当时,S与的交点R满足;④当时,S为六边形;⑤当时,S的面积为.三、解答题8.(本小题满分14分)如图,在四棱锥中,底面为直角梯形,//,,平面底面,为的中点,是棱的中点,(Ⅰ)求证:;(Ⅱ)求直线与平面所成角的正弦值;(Ⅲ)求二面角的余弦值.9.(本小题满分12分)如图,在四棱锥P—ABCD中,PA⊥平面ABCD,底面ABCD为梯形,BC∥AD,AB⊥AD,PA=AB=BC=1,AD=2.2ABCD1A1B1C1D(1)求三棱锥P—ACD的外接球的表面积;(2)若M为PB的中点,问在AD上是否存在一点E,使AM∥平面PCE?若存在,求的值;若不存在,说明理由.10.如图,在三棱锥中,平面平面,于点,且,,(1)求证:(2)(3)若,,求三棱锥的体积.3参考答案1.C【解析】试题分析:根据三视图可知该几何体为一个四棱锥和三棱锥的组合体,如图所示,且平面,平面,底面为正方形,则有,所以和到平面的距离相等,且为,故,,则该几何体的体积为.考点:三视图、简单几何体体积2.A【解析】试题分析:三视图复原的组合体是下部是棱长为2的正方体,上部是底面边长为2的正方形,高为1的四棱锥,组合体的表面积为:,故选A.考点:三视图求几何体的表面积3.A【解析】试题分析:当P、B1重合时,主视图为选项B;当P到B点的距离比B1近时,主视图为选项C;当P到B点的距离比B1远时,主视图为选项D,因此答案为A.考点:组合体的三视图4.D【解析】试题分析:根据题中所给的三视图,可知该几何体为底面是直角梯形,且顶点在底面上的射影是底面梯形的左前方的顶点,所以最长的侧棱应该是棱锥的顶点与右后方的点的侧棱,故根据勾股定理,可知最长侧棱应该是29.,故选D.考点:根据几何体的三视图确定几何体的特征.5.【解析】试题分析:如图所示,经过点的截面为平行四边形设,则,为了求出平行四边形的高,先求的高,由等面积法可得,又由三垂线定理可得平行四边形的高,因此平行四边形的面积,当且仅当时考点:几何体的截面面积的计算6.1324S.【解析】试题分析:四边形ABCD和11AADD的面积分别为4和6,长方体在平面内的射影可由这两个四边形在平面内的射影组合而成.显然,4minS.若记平面ABCD与平面所成角为,则平面11AADD与平面所成角为2.它们在平面内的射影分别为cos4和sin6)2cos(6,所以,)sin(132sin6cos4S(其中,32tan),因此,132maxS,当且仅当2时取到.因此,.考点:三角函数的化简和求值.7.①②③⑤【解析】试题分析:取AB的中点M,在DD1上取点N,使得DN=CQ,则MN∥PQ;作AT∥MN,交直线DD1于点T,则A、P、Q、T四点共面;①当0