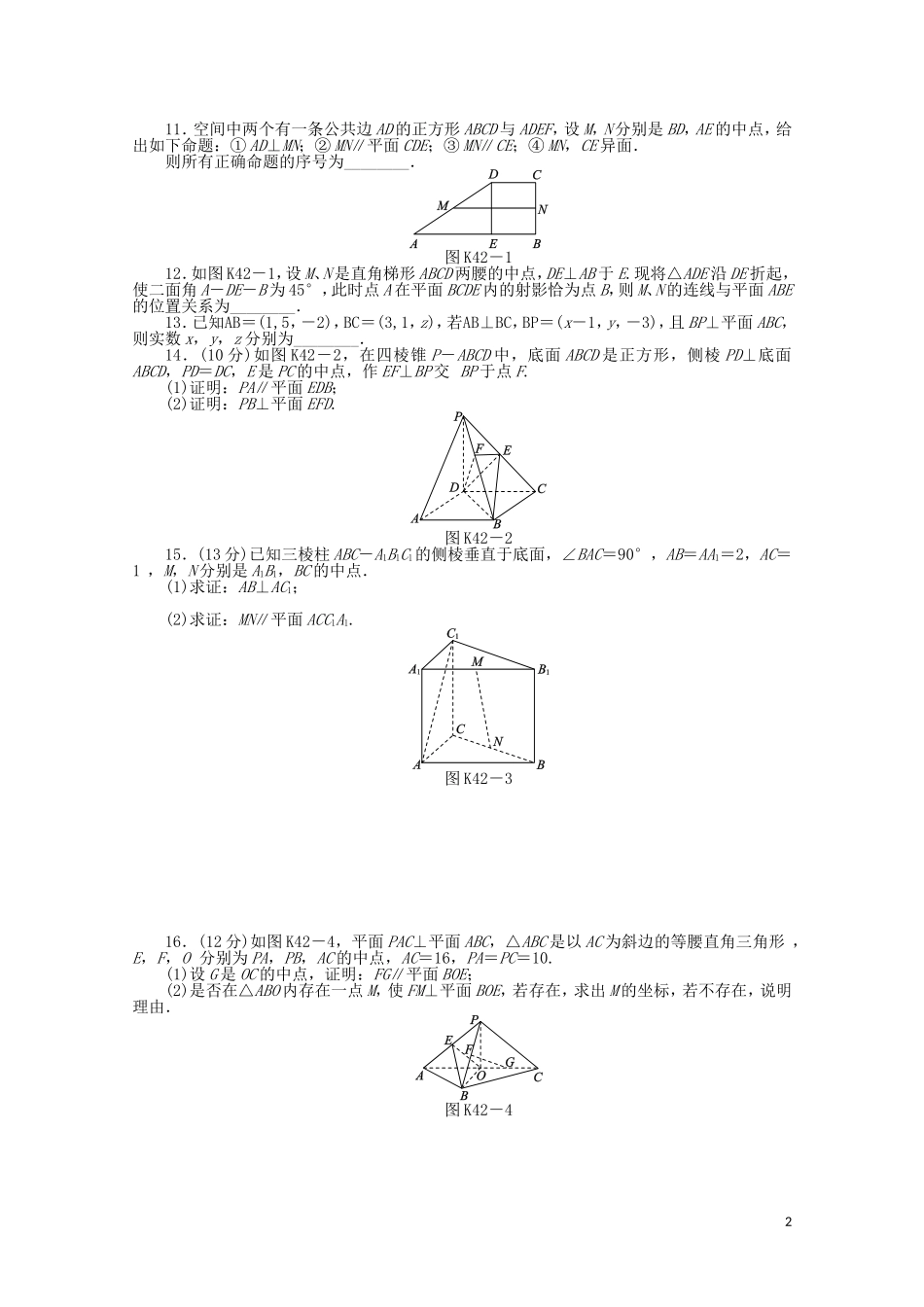
立体几何中向量方法(一)——位置关系的证明1.直线l1,l2相互平行,则下列向量可能是这两条直线的方向向量的是()A.s1=(0,1,2),s2=(2,1,0)B.s1=(0,1,1),s2=(1,1,0)C.s1=(1,1,2),s2=(2,2,4)D.s1=(1,1,1),s2=(-1,2,-1)2.直线l1,l2相互垂直,则下列向量可能是这两条直线的方向向量的是()A.s1=(1,1,2),s2=(2,-1,0)B.s1=(0,1,-1),s2=(2,0,0)C.s1=(1,1,1),s2=(2,2,-2)D.s1=(1,-1,1),s2=(-2,2,-2)3.若直线l∥平面α,直线l的方向向量为s,平面α的法向量为n,则下列结论正确的是()A.s=(-1,0,2),n=(1,0,-1)B.s=(-1,0,1),n=(1,2,-1)C.s=(-1,1,1),n=(1,2,-1)D.s=(-1,1,1),n=(-2,2,2)4.若直线l⊥平面α,直线l的方向向量为s,平面α的法向量为n,则下列结论正确的是()A.s=(1,0,1),n=(1,0,-1)B.s=(1,1,1),n=(1,1,-2)C.s=(2,1,1),n=(-4,-2,-2)D.s=(1,3,1),n=(2,0,-1)5.若平面α,β平行,则下面可以是这两个平面的法向量的是()A.n1=(1,2,3),n2=(-3,2,1)B.n1=(1,2,2),n2=(-2,2,1)C.n1=(1,1,1),n2=(-2,2,1)D.n1=(1,1,1),n2=(-2,-2,-2)6.若平面α,β垂直,则下面可以是这两个平面的法向量的是()A.n1=(1,2,1),n2=(-3,1,1)B.n1=(1,1,2),n2=(-2,1,1)C.n1=(1,1,1),n2=(-1,2,1)D.n1=(1,2,1),n2=(0,-2,-2)7.直线l的方向向量为s=(-1,1,1),平面π的法向量为n=(2,x2+x,-x),若直线l∥平面π,则x的值为()A.-2B.-C.D.±8.已知A(1,0,0),B(0,1,0),C(0,0,1),则平面ABC的单位法向量是()A.s=±(1,1,1)B.s=±C.s=±D.s=±9.已知非零向量a,b及平面α,若向量a是平面α的法向量,则a·b=0是向量b所在直线平行于平面α或在平面α内的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件10.平面α的一个法向量n=(0,1,-1),如果直线l⊥平面α,则直线l的单位方向向量是s=________.111.空间中两个有一条公共边AD的正方形ABCD与ADEF,设M,N分别是BD,AE的中点,给出如下命题:①AD⊥MN;②MN∥平面CDE;③MN∥CE;④MN,CE异面.则所有正确命题的序号为________.图K42-112.如图K42-1,设M、N是直角梯形ABCD两腰的中点,DE⊥AB于E.现将△ADE沿DE折起,使二面角A-DE-B为45°,此时点A在平面BCDE内的射影恰为点B,则M、N的连线与平面ABE的位置关系为________.13.已知AB=(1,5,-2),BC=(3,1,z),若AB⊥BC,BP=(x-1,y,-3),且BP⊥平面ABC,则实数x,y,z分别为________.14.(10分)如图K42-2,在四棱锥P-ABCD中,底面ABCD是正方形,侧棱PD⊥底面ABCD,PD=DC,E是PC的中点,作EF⊥BP交BP于点F.(1)证明:PA∥平面EDB;(2)证明:PB⊥平面EFD.图K42-215.(13分)已知三棱柱ABC-A1B1C1的侧棱垂直于底面,∠BAC=90°,AB=AA1=2,AC=1,M,N分别是A1B1,BC的中点.(1)求证:AB⊥AC1;(2)求证:MN∥平面ACC1A1.图K42-316.(12分)如图K42-4,平面PAC⊥平面ABC,△ABC是以AC为斜边的等腰直角三角形,E,F,O分别为PA,PB,AC的中点,AC=16,PA=PC=10.(1)设G是OC的中点,证明:FG∥平面BOE;(2)是否在△ABO内存在一点M,使FM⊥平面BOE,若存在,求出M的坐标,若不存在,说明理由.图K42-423答案解析【基础热身】1.C[解析]两直线平行则其方向向量平行,根据两向量平行的条件检验知正确选项为C.2.B[解析]两直线垂直,其方向向量垂直,只有选项B中的两个向量垂直.3.C[解析]直线与平面平行,直线的方向向量和平面的法向量垂直,检验知正确选项为C.4.C[解析]线面垂直时,直线的方向向量平行于平面的法向量,只有选项C中的两向量平行.【能力提升】5.D[解析]两个平面平行时其法向量也平行,检验知正确选项为D.6.A[解析]两个平面垂直时其法向量垂直,只有选项A中的两个向量垂直.7.D[解析]线面平行时,直线的方向向量垂直于平面的法向量,故x2-2=0,解得x=±.8.C[解析]先求出平面ABC的一个法向量,再把其单位化.不难求出其一个法向量是n=(1,1,1),单位化得s=±.9.C[解析]...