辽宁省抚顺市六校联合体高一数学上学期期末考试试题-人教版高一全册数学试题VIP免费

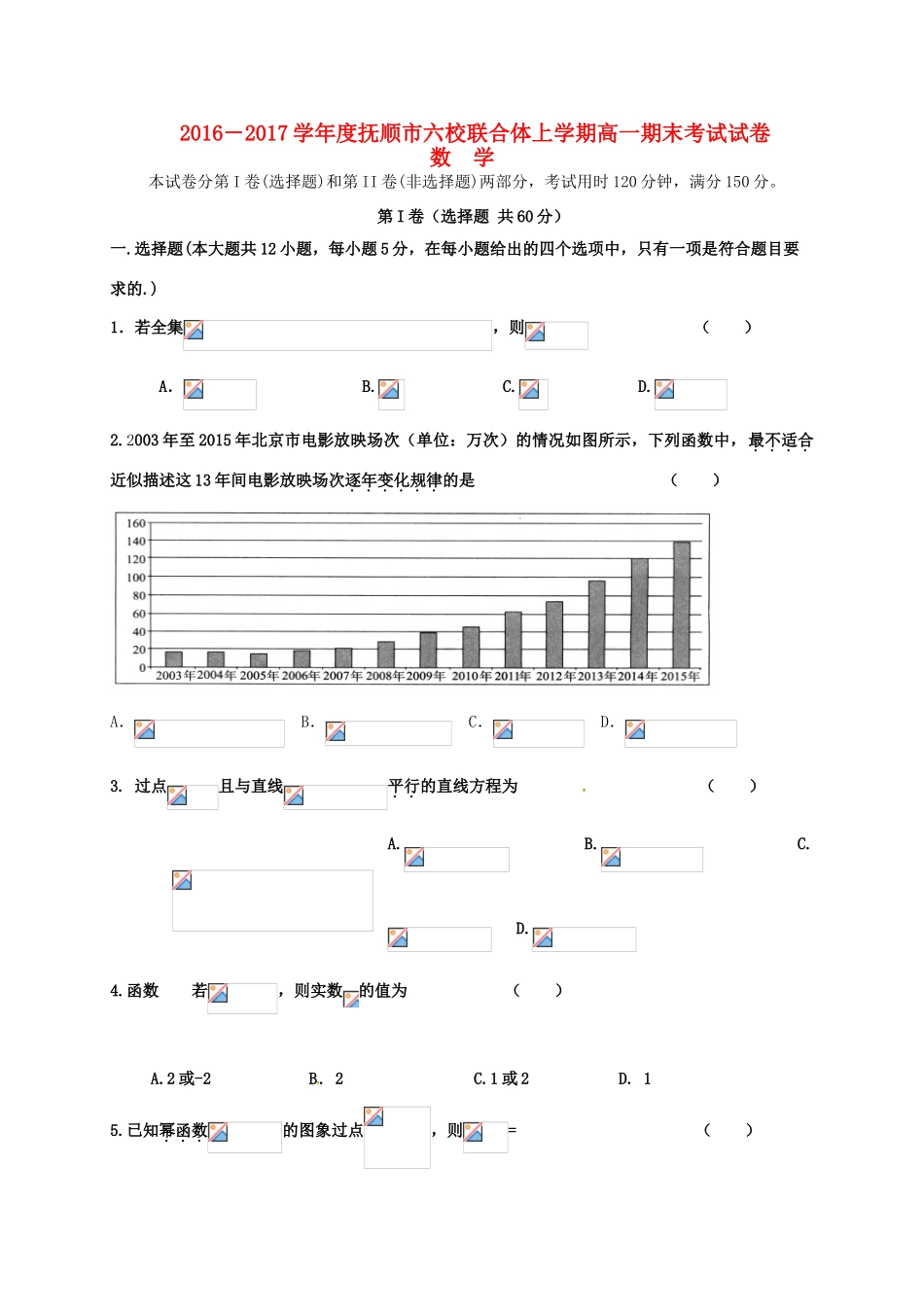
2016－2017学年度抚顺市六校联合体上学期高一期末考试试卷数学本试卷分第I卷(选择题)和第II卷(非选择题)两部分，考试用时120分钟，满分150分。第I卷（选择题共60分）一.选择题(本大题共12小题，每小题5分，在每小题给出的四个选项中，只有一项是符合题目要求的.)1．若全集，则（）A．B.C.D.2.2003年至2015年北京市电影放映场次（单位：万次）的情况如图所示，下列函数中，最不适合近似描述这13年间电影放映场次逐年变化规律的是（）A．B．C．D．3.过点且与直线平行的直线方程为（）A.B.C.D.4.函数若，则实数的值为（）A.2或-2B.2C.1或2D.15.已知幂函数的图象过点，则=（）A.2B.C.8D.6.已知点和点是关于直线对称的两点，则直线的方程为（）A.B.C.D.7.设，则()A.B.C.D.8.设是两个不同的平面，是两条不同的直线，给出下列四个论断①∥；②∥③；④.以其中三个论断作为条件，余下一个论断作为结论，则一共可以写出真命题的个数为（）A．1B．2C．3D．49.一个几何体的三视图如图所示（单位：），那么此几何体的表面积（单位：）是（）A．102B．128C．144D．18410.已知函数是奇函数且当时是减函数，若，则函数的零点共有（）A.4个B.6个C.3个D.5个11．利用“长方体中，四面体”的特点，求得四面体(其中)的外接球的表面积为（）A.B.C.D.12.对于函数，若在其定义域内存在两个实数，当时，的值域也是，则称函数为“Kobe函数”。若函数是“Kobe函数”，则实数的取值范围是（）A.B.C.D.第Ⅱ卷（非选择题共90分）二.填空题（本大题共4道小题，每道小题5分，满分20分.）13.已知集合，且则正数的取值范围是.（用区间表示）14.在中，若将绕直线BC旋转一周，则所形的旋转体的体积是.15．直线和轴，轴分别交于点，以线段为一边在第一象限内作等边，则点的坐标为.16．下列四个命题中，正确的是（写出所有正确命题的序号）①函数的定义域为，则函数的定义域为；②设集合，则在到的所有映射中，偶函数共有4个；③不存在实数，使函数的值域为④函数在上是减函数，则.三.解答题（本大题共6道小题，满分70分，解答应写出文字说明，证明过程或演算步骤.）17.(本小题满分10分)如图，在平行四边形中，过点做⊥，垂足为点，试求所在直线的一般式方程.DBCAO1x32321yFECBDAB1C1D1A118.(本小题满分12分)如图，长方体﹣中，，，,点分别在上，.过点的平面与此长方体的面相交，交线围成一个正方形.（Ⅰ）在图中画出这个正方形（保留画图痕迹，不用说明画法和理由）（Ⅱ）求平面把该长方体分成的两部分中较小部分的体积.19.(本小题满分12分)已知集合（Ⅰ）若,求的取值范围；（Ⅱ）若，求的取值范围.20.(本小题满分12分)为了绿化城市，准备在如图所示的区域内修建一个矩形的草坪，其中,点在上，且∥,⊥,经测量,,,，问应如何设计才能使草坪的占地面积最大？并求出最大面积（精确到1）．21.(本小题满分12分)如图，垂直于矩形所在平面，,垂足为，垂足为.（Ⅰ）设平面，求证：；QABCEDRPMADBCPEFG（Ⅱ）设,是线段的中点，求证：∥平面.22.(本小题满分12分)已知是定义在上的奇函数，且，当时，有.（Ⅰ）证明：在上是增函数；（Ⅱ）解不等式；（Ⅲ）若对任意任意恒成立，求实数的取值范围.2016-2017抚顺市六校联合体上学期高一期末考试数学试题标准答案一、选择题。每小题5分，满分60分.1.A．2.B．3.A．4.B．5.B.6.C.7.C.8.D.9.C.10.D.11.A.12.D二、填空题。每小题5分，满分20分.13..14..15..16.②③④三、解答题,满分70分。17.解：因为点O（0，0），点C（1，3），所以OC所在直线的斜率为.（2分），在中，,因为CD⊥AB，所以CD⊥OC.所以CD所在直线的斜率为.（6分）所以CD所在直线方程为.（10分）18.解：（Ⅰ）交线围成的正方形EHGF如图：在面ABCD中做HG平行于BC,连接EH,FG且HB=GC=6，则EF平行且等于HG，所以四边形EFGH是平行四边形，EF平行于,所以EF垂直面,所以EF垂直于EH,且经过计算可知EH=FG=10，所以EFGH是正方形本问满分6分，按以下三种情况，酌情给分有痕迹，作图正确……6分无痕迹，作图基本正确，比例合理……4分无痕迹，作图大致正确，比例基本合理……2分（Ⅱ）由图形可以看出左半部分体积小……2分，所求几何体的体积...