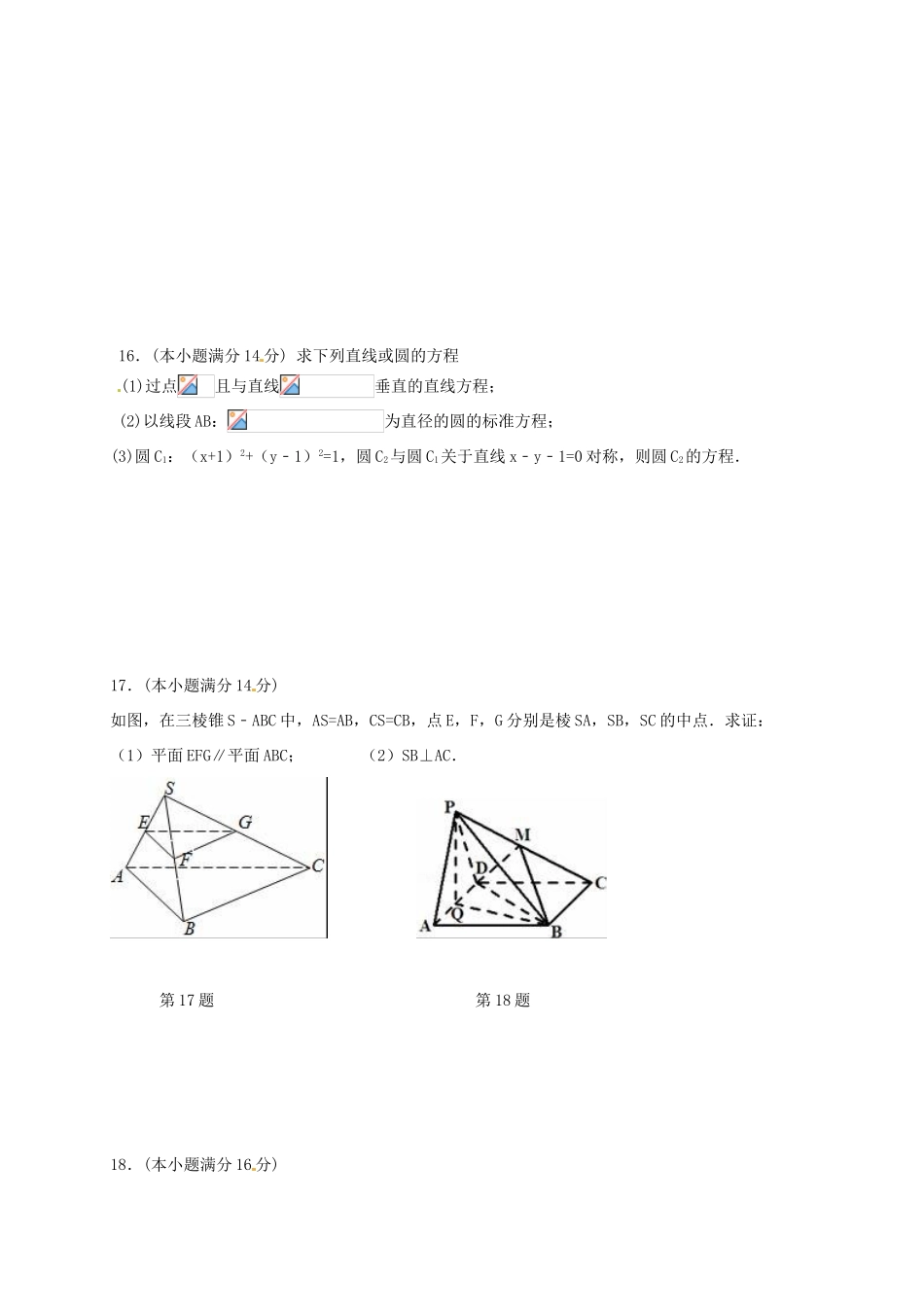
2016—2017学年第二学期期中考试高一年级数学试题一.填空题:本大题共14小题,每小题5分,共计70分﹒请把答案填写在答题纸相应位置上1.用符号表示“点A在平面α内,直线l在平面α内”为▲.2.直线x+y﹣1=0的倾斜角是▲.3.直线l1:x+2y﹣4=0与l2:mx+(2﹣m)y﹣1=0平行,则实数m=▲.4.梯形ABCD中AB∥CD,AB⊂平面α,CD⊄平面α,则直线CD与平面α内的直线的位置关系▲.5.过(﹣5,0),(3,﹣3)两点的直线的方程一般式为▲.6.直线x﹣y﹣5=0被圆x2+y2﹣4x+4y+6=0所截得的弦的长为▲.7.为任意实数时,直线必过的定点坐标为▲.8.在直观图(如图所示)中,四边形O'A'B'C'为菱形且边长为2cm,则在xOy坐标系中,四边形OABC的面积为▲cm2.9.已知m,n是不重合的两条直线,α,β是不重合的两个平面.下列命题:①若α⊥β,m⊥α,则m∥β;②若m⊥α,m⊥β,则α∥β;③若m∥α,n⊥α,则m⊥n;④若m∥α,m⊂β,则α∥β.其中所有真命题的序号是▲.10.已知正四棱锥的底面边长是6,高为,这个正四棱锥的侧面积是▲.11.已知直线过点(2,3),它在x轴上的截距是在y轴上的截距的2倍,则此直线的方程为▲.12.若直线y=﹣x+b与曲线x=恰有一个公共点,则b的取值范围是▲.13.如图,AB为圆O的直径,点C在圆周上(异于点A,B),直线PA垂直于圆O所在的平面,点M是线段PB的中点.有以下四个命题:①MO∥平面PAC;②PA∥平面MOB;③OC⊥平面PAC;④平面PAC⊥平面PBC.其中正确的命题的序号是▲.14.已知圆,点为直线上一点,若圆存在一条弦垂直平分线段,则点的横坐标的取值范围是▲.二.简答题:本大题共6小题,共计90分﹒请在答题卡的指定区域内作答,解答时应写出文字说明,证明过程或演算步骤﹒15.(本小题满分14分)如图,在正三棱柱中,分别为中点.(1)求证:平面;(2)求证:平面平面.ABCA1B1C1FE第15题16.(本小题满分14分)求下列直线或圆的方程(1)过点且与直线垂直的直线方程;(2)以线段AB:为直径的圆的标准方程;(3)圆C1:(x+1)2+(y﹣1)2=1,圆C2与圆C1关于直线x﹣y﹣1=0对称,则圆C2的方程.17.(本小题满分14分)如图,在三棱锥S﹣ABC中,AS=AB,CS=CB,点E,F,G分别是棱SA,SB,SC的中点.求证:(1)平面EFG∥平面ABC;(2)SB⊥AC.第17题第18题18.(本小题满分16分)如图,边长为4的正方形ABCD所在平面与正三角形PAD所在平面互相垂直,M,Q分别为PC,AD的中点,(1)求证:PA∥平面MBD;(2)求四棱锥P﹣ABCD的体积;(3)试问:在线段AB上是否存在一点N,使得平面PCN⊥平面PQB?若存在,试指出点N的位置,并证明你的结论;若不存在,请说明理由.19.(本小题满分16分)已知圆C:(x﹣3)2+(y﹣4)2=4,直线l1过定点A(1,0).(1)若l1与圆C相切,求l1的方程;(2)若l1的倾斜角为,l1与圆C相交于P,Q两点,求线段PQ的中点M的坐标;(3)若l1与圆C相交于P,Q两点,求三角形CPQ的面积的最大值,并求此时l1的直线方程.20.(本小题满分16分)在平面直角坐标系xOy中,设△ABC顶点坐标分别为A(0,a),B(﹣,0),C(,0),Q(0,b),(其中a>0,b>0),圆M为△ABC的外接圆.(1)当a=9时,求圆M的方程;(2)当a变化时,圆M是否过某一定点?若是,求出定点的坐标,若不是,请说明理由;(3)在(1)的条件下,若圆M上存在点P,满足PQ=2PO,求实数b的取值范围.高一数学试题参考答案一.填空题:(1)A∈α,lα⊂(2)(3)(4)平行或异面(5)3x+8y+15=0(6)(7).(8)8(9)②③(10)48(11)3x﹣2y=0或x+2y﹣8=0(12)(13)①④(14)二.简答题:15证:(1)连交于点,为中点,,为中点,,,四边形是平行四边形,…………4分,又平面,平面,平面.………………………………7分(2)由(1)知,,为中点,所以,所以,……9分又因为底面,而底面,所以,则由,得,而平面,且,所以面,………12分又平面,所以平面平面………………14分(说明:其他解法参照给分)16解:(1)………………………………4分(2)………………………………5分(3)(x﹣2)2+(y+2)2=1.………………………………5分17证明:(1) E、G分别为SA、SC的中点,∴EF、EG分别...