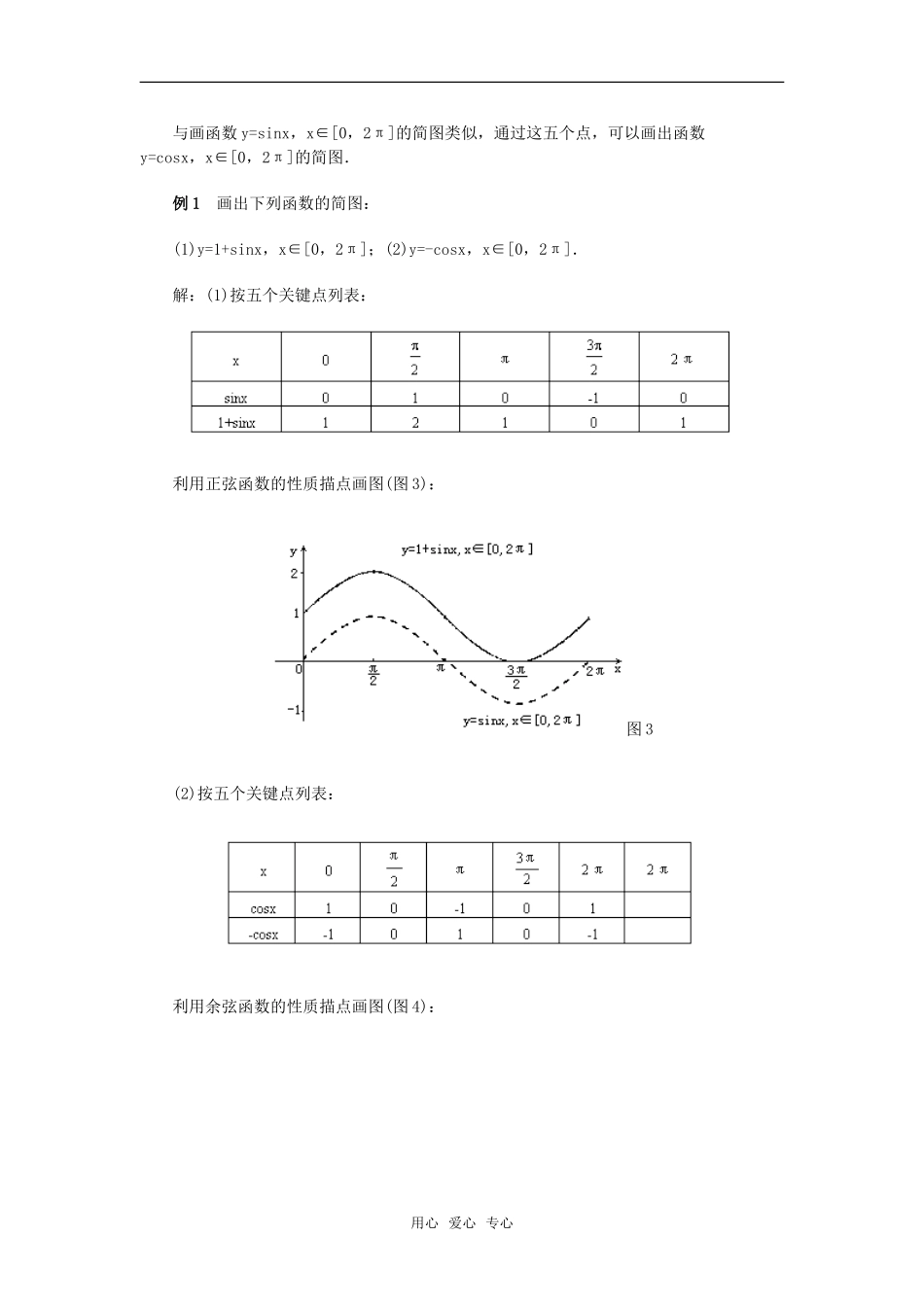
正弦函数图象的两种作图法一、根据正弦线画正弦函数的图象现在我们利用正弦线画出正弦函数的图象.在直角坐标系的x轴上任意取一点O1,以O1为圆心作单位圆(图4-19),从⊙O1与x轴的交点A起把⊙O1分成12等份(份数宜取6的倍数,份数越多,画出的图象越精确).过⊙O1上的各分点作x轴的垂线,的点).把角x的正弦线向右平移,使它的起点与x轴上的点x重合(例如,线把这些正弦线的终点连结起来,就得到了函数y=sinx,x∈[0,2π]的图象(图1).图1因为终边相同的角有相同的三角函数值,所以函数y=sinx,x∈[2kπ,2(k+1)π),k∈Z且k≠0的图象,与函数y=sinx,x∈[0,2π)的图象的形状完全一样,只是位置不同.于是我们只要将函数y=sinx,x∈[0,2π)的图象向左、右平行移动(每次2π个单位长度),就可以得到正弦函数y=sinx,x∈R的图象(图4-20).正弦函数的图象叫做正弦曲线.二、“五点(画图)法”由图可以看出,在函数y=sinx,x∈[0,2π]的图象上,起着关键作用的点有以下五个:用心爱心专心事实上,描出这五个点后,函数y=sinx,x∈[0,2π]的图象的形状就基本上确定了.因此,在精确度要求不太高时,我们常常先找出这五个关键点,然后用光滑曲线将它们连结起来,就得到函数的简图.今后,我们将经常使用这种近似的“五点(画图)法”.图2三、余弦函数图象的画法下面我们看余弦函数图象的一种画法.先设法找到函数y=cosx,x∈R与正弦函数的关系:y=cosx由此可以看出:余弦函数y=cosx,x∈R与函数个单位长度而得到(图2).余弦函数的图象叫做余弦曲线.由图2还可以看出,在函数y=cosx,x∈[0,2π]的图象上,起着关键作用的点是以下五个:用心爱心专心与画函数y=sinx,x∈[0,2π]的简图类似,通过这五个点,可以画出函数y=cosx,x∈[0,2π]的简图.例1画出下列函数的简图:(1)y=1+sinx,x∈[0,2π];(2)y=-cosx,x∈[0,2π].解:(1)按五个关键点列表:利用正弦函数的性质描点画图(图3):图3(2)按五个关键点列表:利用余弦函数的性质描点画图(图4):用心爱心专心图4注(1)第(1)小题中的函数与函数y=sinx,x∈6[0,2π]有什么关系呢?我们把后者的图象用虚线画在图4-21中,可见函数y=1+sinx,x∈[0,2π]的图象可通过把函数y=sinx,x∈[0,2π]的图象上的每一点向上平行移动1个单位长度而得到.(2)第(2)小题中的函数与函数y=cosx,x∈[0,2π]有什么关系呢?我们把后者的图象用虚线画在图4-22中,可见函数y=-cosx,x∈[0,2π]的图象与函数y=cosx,x∈[0,2π]的图象关于X轴对称.用心爱心专心