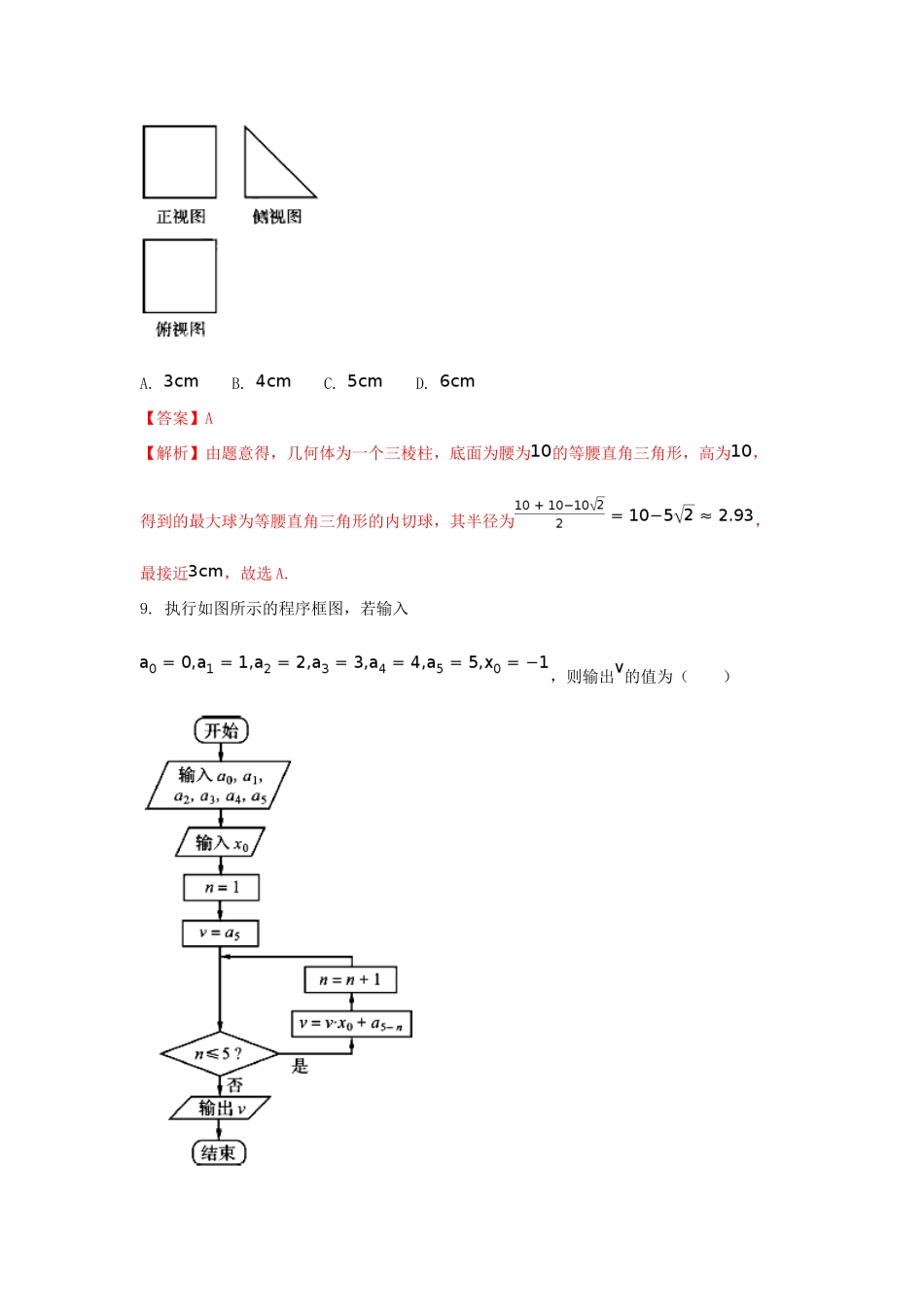
四川省资阳市2017届高三数学上学期期末考试试卷理(含解析)第Ⅰ卷(选择题共60分)一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.1.设集合,则()A.B.C.D.【答案】B【解析】由题意得,,则,故选B.2.为虚数单位,已知复数满足,则()A.B.C.D.【答案】C【解析】由题意得,设,则,,故选C.3.下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是()A.230.5,220B.231.5,232C.231,231D.232,231【答案】C【解析】由题意得,连续多天同一路口同一时段通过车辆的数目分别为,中位数为,众数为,故选C.4.在的展开式中,各二项式系数之和为64,则展开式中常数项为()A.135B.105C.30D.15【答案】A【解析】由二项式系数的性质,得,则的展开式为,则,展开式中常数项为135,故选A.5.已知向量满足,向量与的夹角为60°,则()A.B.19C.D.7【答案】C【解析】由题意得,,则选C.6.已知,则的值为()A.B.1C.D.【答案】A【解析】由题意得,,则,故选A.7.四个数的大小顺序是()A.B.C.D.【答案】D【解析】由题意得,,故选D.8.一块硬质材料的三视图如图所示,正视图和俯视图都是边长为的正方形,将该木料切削、打磨,加工成球,则能得到的最大球的半径最接近()A.B.C.D.【答案】A【解析】由题意得,几何体为一个三棱柱,底面为腰为的等腰直角三角形,高为,得到的最大球为等腰直角三角形的内切球,其半径为,最接近,故选A.9.执行如图所示的程序框图,若输入,则输出的值为()A.15B.3C.-3D.-15【答案】C【解析】由题意得,当时,跳出循环,则,故选C.10.在中,,若,则向量在上的投影是()A.B.C.D.【答案】B【解析】由正弦定理得,,由余弦定理得,,则,故选B.11.已知双曲线的右顶点为,抛物线的焦点为.若在的渐近线上存在点,使得,则的离心率的取值范围是()A.B.C.D.【答案】B【解析】由题意得,,设,由,得,因为在的渐近线上存在点,则,即,又因为为双曲线,则,故选B.【点睛】本题主要考查了双曲线的基本性质的应用,抛物线基本性质的应用,向量数量积坐标运算以及一元二次方程根的判别式的运用,属于中档题,首先可画一张草图,分析其中的几何关系,然后将系用代数形式表示出来,即可得到一个一元二次方程,若要使得一元二次方程有实数解,,水到渠成,即可得到答案,因此将几何关系转化成方程是解题的关键.12.设集合,那么集合中满足条件“”的元素个数为()A.60B.65C.80D.81【答案】D【解析】由题意可得,成立,需要分五种情况讨论:当时,只有一种情况,即;当时,即,有种;当时,即,有种;当时,即,有种当时,即,有种,综合以上五种情况,则总共为:种,故选D.【点睛】本题主要考查了创新型问题,往往涉及方程,不等式,函数等,对涉及的不同内容,先要弄清题意,看是先分类还是先步,再处理每一类或每一步,本题抓住只能取相应的几个整数值的特点进行分类,对于涉及多个变量的排列,组合问题,要注意分类列举方法的运用,且要注意变量取值的检验,切勿漏掉特殊情况.第Ⅱ卷(非选择题共90分)二、填空题:本大题共4小题,每小题5分,满分20分,将答案填在答题纸上13.已知实数满足,则的最大值是__________.【答案】【解析】由约束条件可作如图所示的可行域,两直线的交点,则当过原点的直线过点时,斜率最大,即的最大值为.14.将函数的图象向左平移个单位,再将所得图象上各点的横坐标缩为原来的,纵坐标不变,便得到函数的图象,则解析式为__________.【答案】【解析】由题意得,当函数的图象向左平移个单位,则,将所得图象上各点的横坐标缩为原来的,纵坐标不变,则,即答案为.15.若直线(都是正实数)与圆相交于两点,当(是坐标原点)的面积最大时,的最大值为__________.【答案】2【解析】根据题意画出图形,如图所示:由的面积为可得,为直角三角形,,则点到直线的距离为,即,那么只有当且仅当时,取最大值.16.已知函数,若函数在处的切线与函数的图象恰好只有3个公共点,则的取值范围是__________.【答案】【解析】由题意得,当时,直线的方程为:,其与时的...