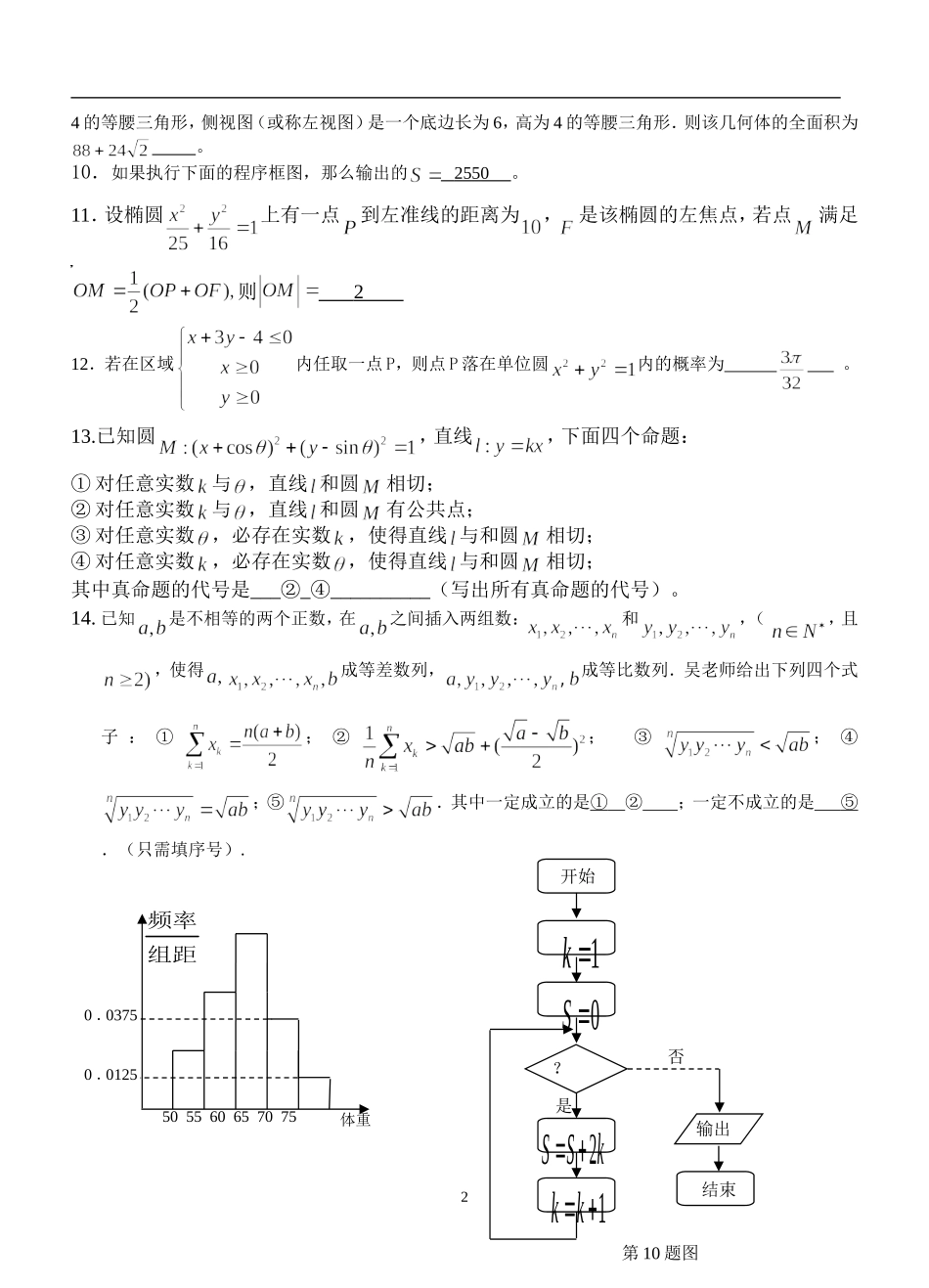
江苏东海进修学校高补班数学模拟测试卷班级姓名得分2008.1.10一、填空题:(5×14=70分)1.已知全集,,,则=2.已知函数的图象在点处的切线方程是,则3.3.已知,,,则与夹角的度数为。4.i是虚数单位,.(用a+bi的形式表示,a,b∈R)5.用二分法求函数的一个零点,其参考数据如下:f(1.6000)=0.200f(1.5875)=0.133f(1.5750)=0.067f(1.5625)=0.003f(1.5562)=-0.029f(1.5500)=-0.060据此数据,可得方程的一个近似解(精确到0.01)为1.5593.6.为了了解高三学生的身体状况.抽取了部分男生的体重,将所得的数据整理后,画出了频率分布直方图(如下图),已知图中从左到右的前3个小组的频率之比为1︰2︰3,第2小组的频数为12,则抽取的男生人数是48.7.函数若,则的所有可能值组成的集合为8.某医疗研究所为了检验某种血清预防感冒的作用,把名使用血清的人与另外名未用血清的人一年中的感冒记录作比较,提出假设:“这种血清不能起到预防感冒的作用”,利用列联表计算得,经查对临界值表知.则下列结论中,正确结论的序号是①.①有的把握认为“这种血清能起到预防感冒的作用”;②若某人未使用该血清,那么他在一年中有的可能性得感冒;③这种血清预防感冒的有效率为;④这种血清预防感冒的有效率为.9.已知某几何体的俯视图是如图所示(图在下面)的矩形,正视图(或称主视图)是一个底边长为8,高为14的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.则该几何体的全面积为。10.如果执行下面的程序框图,那么输出的2550。11.设椭圆上有一点到左准线的距离为,是该椭圆的左焦点,若点满足则212.若在区域内任取一点P,则点P落在单位圆内的概率为。13.已知圆,直线,下面四个命题:①对任意实数与,直线和圆相切;②对任意实数与,直线和圆有公共点;③对任意实数,必存在实数,使得直线与和圆相切;④对任意实数,必存在实数,使得直线与和圆相切;其中真命题的代号是___②_④__________(写出所有真命题的代号)。14.已知是不相等的两个正数,在之间插入两组数:和,(,且,使得成等差数列,成等比数列.吴老师给出下列四个式子:①;②;③;④;⑤.其中一定成立的是①②;一定不成立的是⑤.(只需填序号).2体重505560657075频率组距0.03750.0125开始1k0S?是2SSk1kk否输出结束第10题图第6题图二、解答题:(90分)15.(本题满分12分)分别是中的对边,其外接圆半径为1,且,边是关于x的方程:的两根()(1)求的度数及边的值(2)判定的形状,并求其内切圆的半径解(1)b、c是的两根,且b>c故b=2,c=1.又(2)由是直角三角形.16.(本小题满分14分)平面内有向量,,,点是直线上一动点.(是坐标原点)(Ⅰ)求的最小值,并求此时的坐标;(Ⅱ)设与的夹角为,当取得最小值时,求的值.解(Ⅰ):由题意:与共线,设,,则,,,3第9题图∴∴当时,取得最小值,此时.(Ⅱ)由(Ⅰ)知:当取得最小值时,,,∴,,∴,∴.17.(本小题满分14分)如图,在四棱锥中,侧面是正三角形,且与底面垂直,底面是边长为的菱形,,是中点,截面交于.(Ⅰ)求证:;(Ⅱ)求证:⊥平面;(Ⅲ)求三棱锥的体积.证明(Ⅰ) ,平面,∴平面, 平面,平面平面,∴.(Ⅱ)取的中点,连结,,, 和都是正三角形,∴,,又,∴平面,又平面,∴, ,是中点,∴,又,4ACBDMNP∴⊥平面.解(Ⅲ) 侧面底面,侧面底面,∴底面. 是边长为2的正三角形,∴, 是边长为2的正三角形,∴,∴三棱锥的体积.……14分18.(本题满分16分)下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据.x3456y2.5344.5(1)请画出上表数据的散点图;(2)请根据上表提供的数据,用最小二乘法求出y关于x的线性回归方程;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的线性回归方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(公式:,)解(1)散点图略(2);所求的回归方程为(3),预测生产100吨甲产品的生产能耗比技改前降低(吨)519.(本小题满分16...