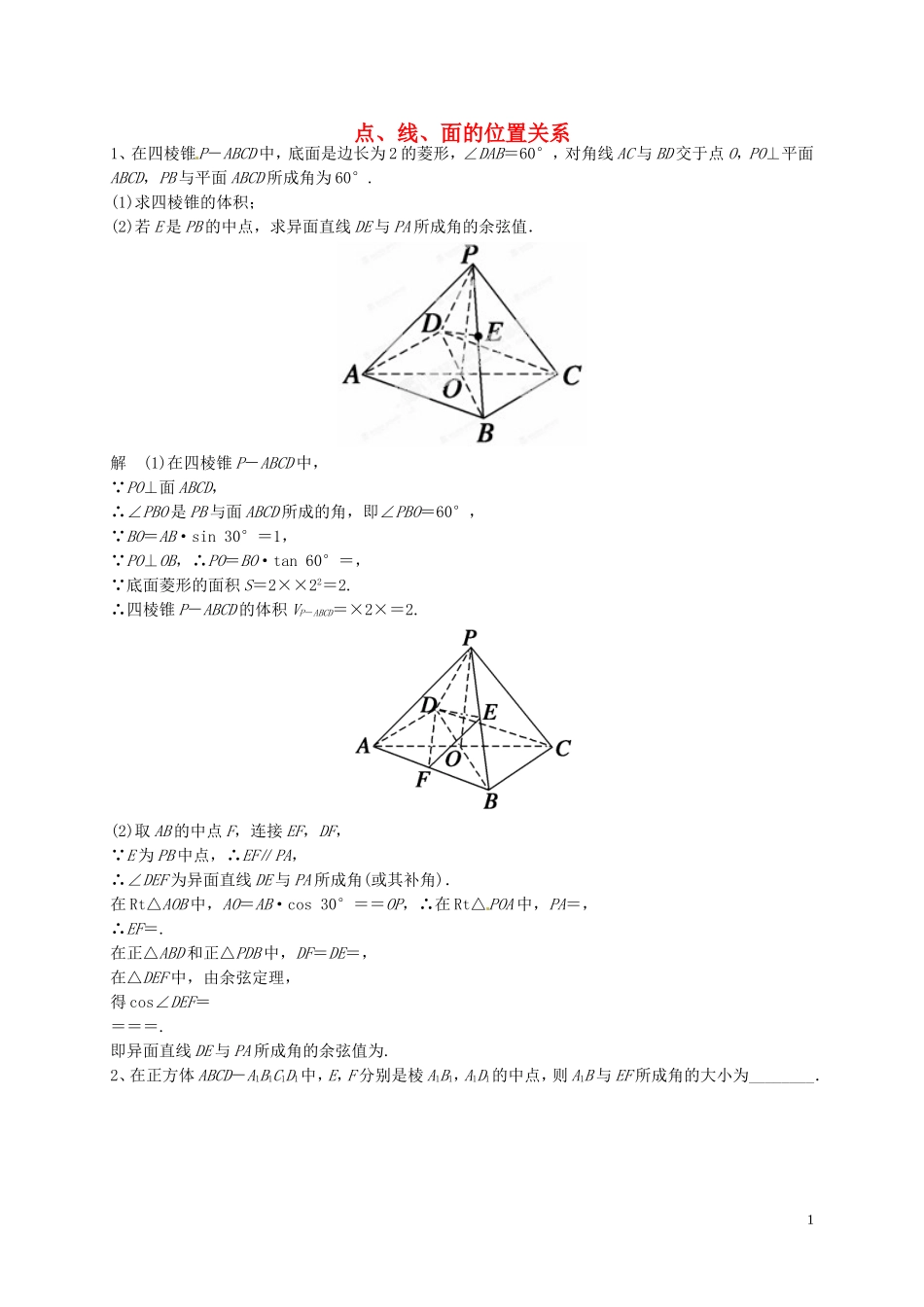
点、线、面的位置关系1、在四棱锥P-ABCD中,底面是边长为2的菱形,∠DAB=60°,对角线AC与BD交于点O,PO⊥平面ABCD,PB与平面ABCD所成角为60°.(1)求四棱锥的体积;(2)若E是PB的中点,求异面直线DE与PA所成角的余弦值.解(1)在四棱锥P-ABCD中, PO⊥面ABCD,∴∠PBO是PB与面ABCD所成的角,即∠PBO=60°, BO=AB·sin30°=1, PO⊥OB,∴PO=BO·tan60°=, 底面菱形的面积S=2××22=2.∴四棱锥P-ABCD的体积VP-ABCD=×2×=2.(2)取AB的中点F,连接EF,DF, E为PB中点,∴EF∥PA,∴∠DEF为异面直线DE与PA所成角(或其补角).在Rt△AOB中,AO=AB·cos30°==OP,∴在Rt△POA中,PA=,∴EF=.在正△ABD和正△PDB中,DF=DE=,在△DEF中,由余弦定理,得cos∠DEF====.即异面直线DE与PA所成角的余弦值为.2、在正方体ABCD-A1B1C1D1中,E,F分别是棱A1B1,A1D1的中点,则A1B与EF所成角的大小为________.1解析如图,连接B1D1,D1C,B1C.由题意知EF是△A1B1D1的中位线,所以EF∥B1D1.又A1B∥D1C,所以A1B与EF所成的角等于B1D1与D1C所成的角.因为△D1B1C为正三角形,所以∠B1D1C=.故A1B与EF所成角的大小为.答案3.(2013·浙江卷)设m,n是两条不同的直线,α,β是两个不同的平面().A.若m∥α,n∥α,则m∥nB.若m∥α,m∥β,则α∥βC.若m∥n,m⊥α,则n⊥αD.若m∥α,α⊥β,则m⊥β解析本题可借助特殊图形求解,画一个正方体作为模型(如图).设底面ABCD为α,侧面A1ADD1为β.①当A1B1=m,B1C1=n时,显然A不正确;②当B1C1=m时,显然D不正确;③当B1C1=m时,显然B不正确.故选C.答案C4.对于不同的直线m,n和不同的平面α,β,γ,有如下四个命题:①若m∥α,m⊥n,则n⊥α;②若m⊥α,m⊥n,则n∥α;③若α⊥β,γ⊥β,则α∥γ;④若m⊥α,m∥n,n⊂β,则α⊥β.其中真命题的个数是().A.1B.2C.3D.4解析本题可借助特殊图形求解.画一个正方体作为模型(如图)设底面ABCD为α.①当A1B1=m,B1C1=n,显然符合①的条件,但结论不成立;②当A1A=m,AC=n,显然符合②的条件,但结论不成立;2③与底面ABCD相邻两个面可以两两垂直,但任何两个都不平行;④由面面垂直的判定定理可知,④是正确的.只有④正确,故选A.答案A5.已知l,m,n是空间中的三条直线,命题p:若m⊥l,n⊥l,则m∥n;命题q:若直线l,m,n两两相交,则直线l,m,n共面,则下列命题为真命题的是().A.p∧qB.p∨qC.p∨(q)D.(p)∧q解析命题p中,m,n可能平行、还可能相交或异面,所以命题p为假命题;命题q中,当三条直线交于三个不同的点时,三条直线一定共面,当三条直线交于一点时,三条直线不一定共面,所以命题q也为假命题.所以p和q都为真命题,故p∨(q)为真命题.选C.答案C4.如图,在正方体ABCD-A1B1C1D1中,(1)求A1C1与B1C所成角的大小;(2)若E,F分别为AB,AD的中点,求A1C1与EF所成角的大小.解:(1)如图,连接AC,AB1,由ABCD-A1B1C1D1是正方体,知AA1C1C为平行四边形,所以AC∥A1C1,从而B1C与AC所成的角就是A1C1与B1C所成的角.由△AB1C中,由AB1=AC=B1C可知∠B1CA=60°,即A1C1与B1C所成角为60°.(2)如图,连接BD,由(1)知AC∥A1C1.∴AC与EF所成的角就是A1C1与EF所成的角. EF是△ABD的中位线,∴EF∥BD.又 AC⊥BD,∴AC⊥EF,即所求角为90°.∴EF⊥A1C1.即A1C1与EF所成的角为90°.直线、平面平行的判定与性质3考点:有关线面、面面平行的命题真假判断1、(1)(2013·广东卷)设m,n是两条不同的直线,α,β是两个不同的平面,下列命题中正确的是().A.若α⊥β,m⊂α,n⊂β,则m⊥nB.若α∥β,m⊂α,n⊂β,,则m∥nC.若m⊥n,m⊂α,n⊂β,则α⊥βD.若m⊥α,m∥n,n∥β,则α⊥β(2)设m,n表示不同直线,α,β表示不同平面,则下列结论中正确的是().A.若m∥α,m∥n,则n∥αB.若m⊂α,n⊂β,m∥β,n∥α,则α∥βC.若α∥β,m∥α,m∥n,则n∥βD.若α∥β,m∥α,n∥m,n⊄β,则n∥β解析(1)A中,m与n可垂直、可异面、可平行;B中m与n可平行、可异面;C中,若α∥β,仍然满足m⊥n,m⊂α,n⊂β,故C...