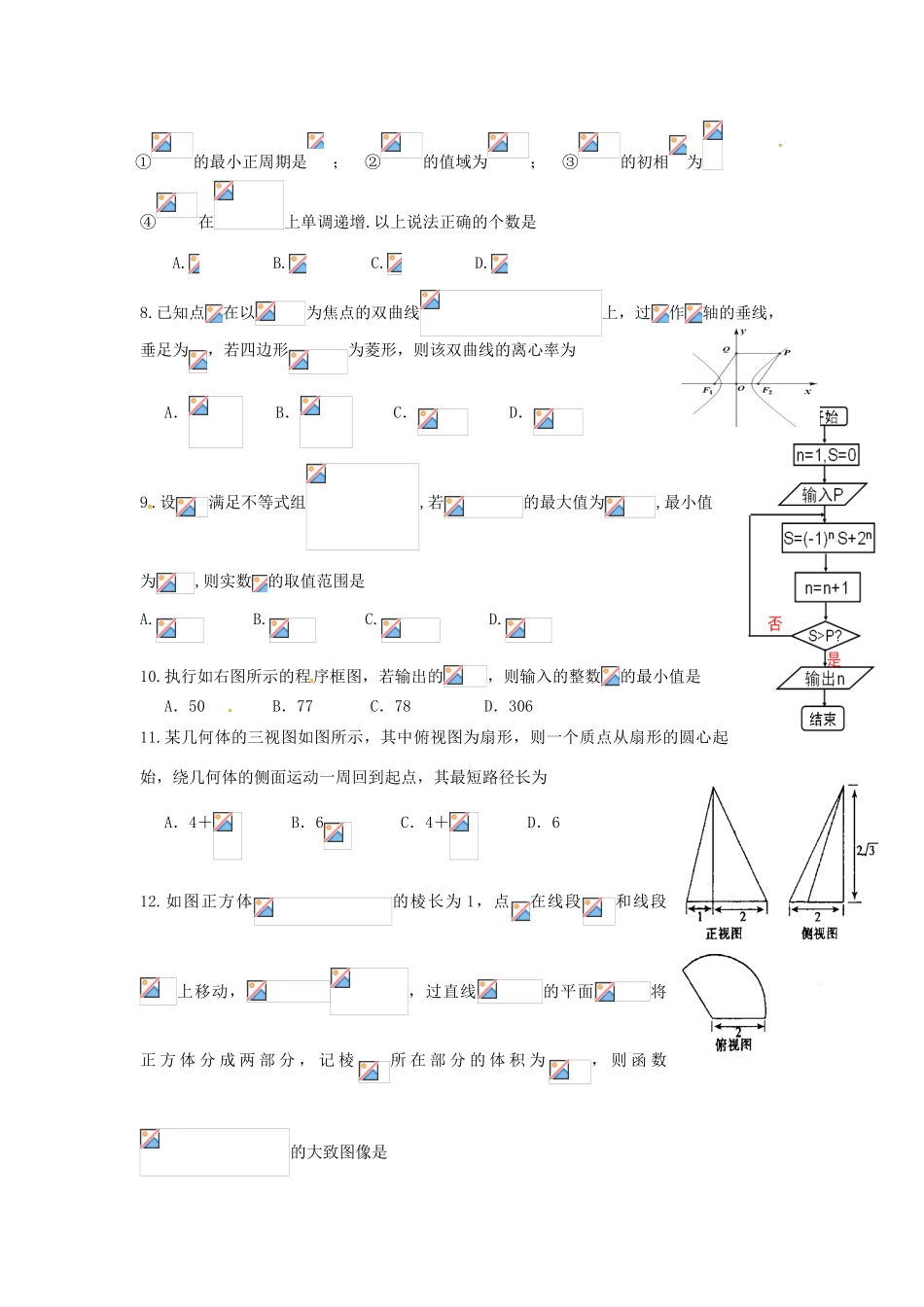
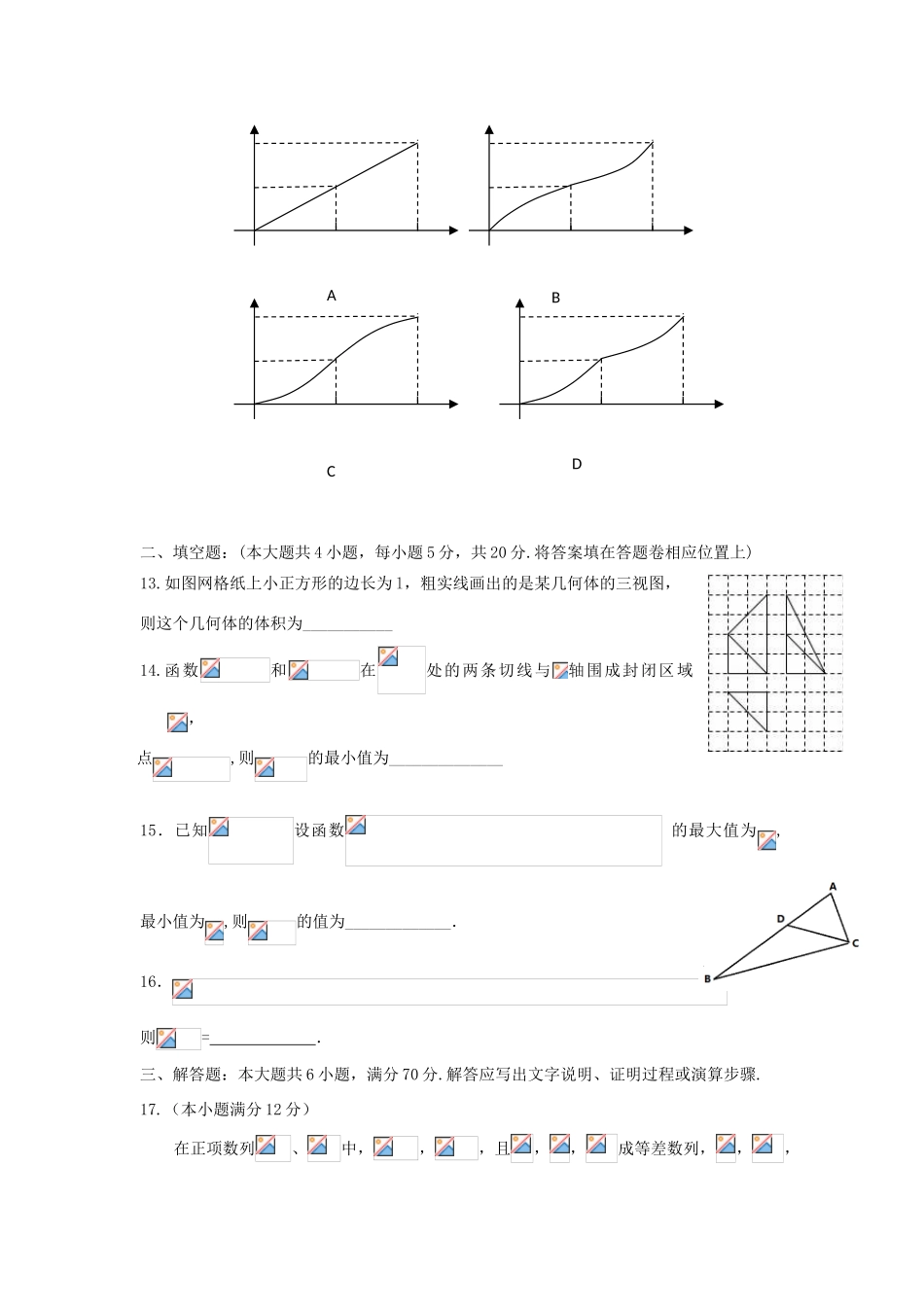
2016届“六校联盟”高考模拟文科数学试题(A卷)一、选择题(本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.已知全集,,,则A.B.C.D.2.已知复数,若为实数,则=A.2B.-2C.-D.3.下列四个函数中,既是偶函数又在上为增函数的是A.B.C.D.4.是半径为2的圆内一个定点,是圆上的一个动点,线段的垂直平分线与半径相交于点,则的最大值为A.1B.2C.3D.45.在2015年全国青运会火炬传递活动中,有编号为1,2,3,4,5的5名火炬手,若从中任选2人,则选出的火炬手的编号不相连的概率为A.B.C.D.6.已知,与不共线,向量与互相垂直,则实数的值为A.B.C.D.7.点是函数的图象的一个对称中心,且点到该图象的对称轴的距离的最小值为.①的最小正周期是;②的值域为;③的初相为④在上单调递增.以上说法正确的个数是A.B.C.D.8.已知点在以为焦点的双曲线上,过作轴的垂线,垂足为,若四边形为菱形,则该双曲线的离心率为A.B.C.D.9.设满足不等式组,若的最大值为,最小值为,则实数的取值范围是A.B.C.D.10.执行如右图所示的程序框图,若输出的,则输入的整数的最小值是A.50B.77C.78D.30611.某几何体的三视图如图所示,其中俯视图为扇形,则一个质点从扇形的圆心起始,绕几何体的侧面运动一周回到起点,其最短路径长为A.4+B.6C.4+D.612.如图正方体的棱长为1,点在线段和线段上移动,,过直线的平面将正方体分成两部分,记棱所在部分的体积为,则函数的大致图像是ABCD二、填空题:(本大题共4小题,每小题5分,共20分.将答案填在答题卷相应位置上)13.如图网格纸上小正方形的边长为l,粗实线画出的是某几何体的三视图,则这个几何体的体积为___________14.函数和在处的两条切线与轴围成封闭区域,点,则的最小值为______________15.已知设函数的最大值为,最小值为,则的值为_____________.16.,则=.三、解答题:本大题共6小题,满分70分.解答应写出文字说明、证明过程或演算步骤.17.(本小题满分12分)在正项数列、中,,,且,,成等差数列,,,成等比数列.(1)证明:成等差数列,并求出,;(2)设,求数列的前和.18.(本题满分12分)在某次足球比赛中,对甲、乙两队上场的13名球员(包括10名首发和3名替补登场(守门员除外))的跑动距离(单位:)进行统计分析,得到的统计结果如茎叶图所示,其中茎表示整数部分,叶表示小数部分.(1)根据茎叶图求两队球员跑动距离的中位数和平均值(精确到小数点后两位),并给出一个正确的统计结论;(2)规定跑动距离为及以上的球员为优秀球员,跑动距离为及以上的球员为积极球员,其余为一般球员.现从两队的优秀球员中随机抽取2名,求这2名球员中既有甲队球员又有乙队球员的概率.19.(本题满分12分)如图,在多面体中,均为直角梯形,,为平行四边形,平面平面.(1)求证:平面;(2)若是边长为2的等边三角形,且与平面所成角的正切值为1,求点到平面的距离.20.(本小题满分12分)已知抛物线的焦点为,过且倾斜角为的直线被抛物线截得的线段长为8.(1)求抛物线的方程;(2)已知直线和抛物线交于点,线段的中点为,在的延长线上任取一点作抛物线的切线,两切点分别为,直线交抛物线于另一点,问直线的斜率是否为定值?若是,求出的值;若不是,请说明理由.21.(本小题满分12分)已知函数(),其导函数为.(1)求函数的极值;(2)当时,关于的不等式恒成立,求的取值范围.请考生在第22,23,24题中任选一题做答,如果多做,则按所做的第一题计分,做答时请写清题号.22.(本小题满分10分)选修4—1:几何证明选讲如图,圆与圆交于两点,以为切点作两圆的切线分别交圆和圆于两点,延长交圆于点,延长交圆于点.已知.(1)求的长;(2)求.23.(本小题满分10)选修4—4:坐标系与参数方程极坐标系的极点为直角坐标系的原点,极轴为轴的正半轴,两种坐标系中的长度单位相同,已知曲线的极坐标方程为,斜率为的直线交轴于点.(1)求的直角坐标方程,的参数方程;(2)直线与曲线交于两点,求的值.24.(本小题满分10分)选修4—5:不等式选讲设函数的最大值.(1)求实数的值;(2)求关于的不等式的解集.2016届“六校...