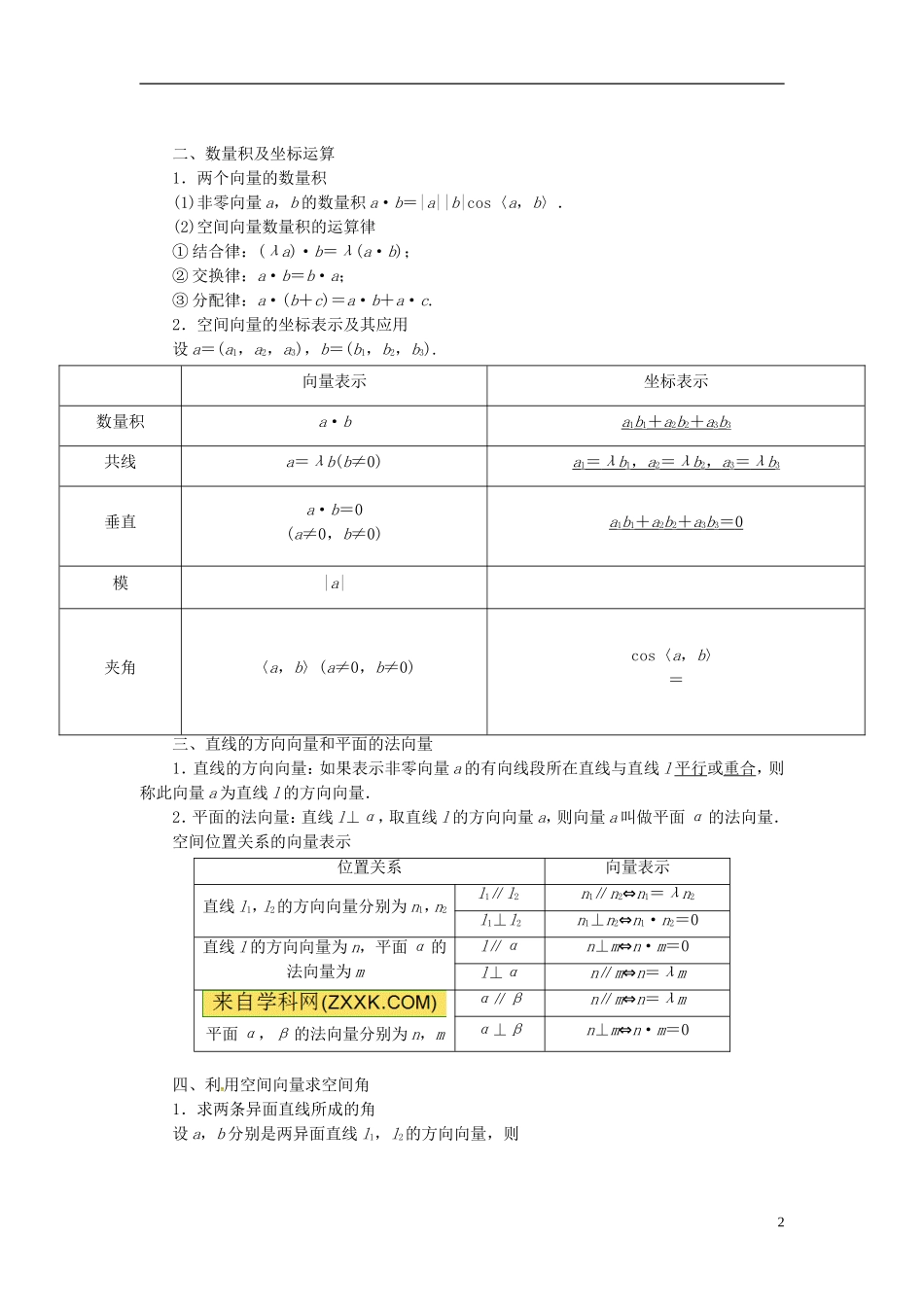
第三讲空间向量与立体几何一、空间向量的有关概念及定理1.空间向量的有关概念(1)空间向量:在空间中,具有大小和方向的量叫做空间向量,其大小叫做向量的长度或模.(2)相等向量:方向相同且模相等的向量.(3)共线向量:如果表示空间向量的有向线段所在的直线平行或重合,则这些向量叫做共线向量或平行向量,a平行于b记作a∥b.(4)共面向量:平行于同一平面的向量叫做共面向量.2.空间向量中的有关定理(1)共线向量定理:对空间任意两个向量a,b(b≠0),a∥b⇔存在λ∈R,使a=λb.(2)共面向量定理:若两个向量a、b不共线,则向量p与向量a,b共面⇔存在唯一的有序实数对(x,y),使p=xa+yb.(3)空间向量基本定理:如果三个向量a、b、c不共面,那么对空间任一向量p,存在一个唯一的有序实数组{x,y,z}使得p=xa+yb+zc.应用共线向量定理、共面向量定理证明点共线、点共面的方法比较:三点(P,A,B)共线空间四点(M,P,A,B)共面PA=λPB且同过点PMP=xMA+yMB对空间任一点O,OP=OA+tAB对空间任一点O,OP=OM+xMA+yMB对空间任一点O,OP=xOA+(1-x)OB对空间任一点O,OP=xOM+yOA+(1-x-y)OB1二、数量积及坐标运算1.两个向量的数量积(1)非零向量a,b的数量积a·b=|a||b|cos〈a,b〉.(2)空间向量数量积的运算律①结合律:(λa)·b=λ(a·b);②交换律:a·b=b·a;③分配律:a·(b+c)=a·b+a·c.2.空间向量的坐标表示及其应用设a=(a1,a2,a3),b=(b1,b2,b3).向量表示坐标表示数量积a·ba1b1+a2b2+a3b3共线a=λb(b≠0)a1=λb1,a2=λb2,a3=λb3垂直a·b=0(a≠0,b≠0)a1b1+a2b2+a3b3=0模|a|夹角〈a,b〉(a≠0,b≠0)cos〈a,b〉=三、直线的方向向量和平面的法向量1.直线的方向向量:如果表示非零向量a的有向线段所在直线与直线l平行或重合,则称此向量a为直线l的方向向量.2.平面的法向量:直线l⊥α,取直线l的方向向量a,则向量a叫做平面α的法向量.空间位置关系的向量表示位置关系向量表示直线l1,l2的方向向量分别为n1,n2l1∥l2[n1∥n2⇔n1=λn2l1⊥l2n1⊥n2⇔n1·n2=0直线l的方向向量为n,平面α的法向量为ml∥αn⊥m⇔n·m=0l⊥αn∥m⇔n=λm平面α,β的法向量分别为n,mα∥βn∥m⇔n=λmα⊥βn⊥m⇔n·m=0四、利用空间向量求空间角1.求两条异面直线所成的角设a,b分别是两异面直线l1,l2的方向向量,则2l1与l2所成的角θa与b的夹角〈a,b〉范围0<θ≤0<〈a,b〉<π关系cosθ=|cos〈a,b〉|=cos〈a,b〉=2.求直线与平面所成的角设直线l的方向向量为a,平面α的法向量为n,直线l与平面α所成的角为θ,则sinθ=|cos〈a,n〉|=.3.求二面角的大小(1)若AB、CD分别是二面角α-l-β的两个面内与棱l垂直的异面直线,则二面角的大小就是向量AB与CD的夹角(如图7-7-1①).图7-7-1(2)设n1,n2分别是二面角α-l-β的两个面α,β的法向量,则向量n1与n2的夹角(或其补角)的大小就是二面角的平面角的大小(如图7-7-1②③).利用空间向量求点面距离如图,已知AB为平面α的一条斜线段,n为平面α的法向量,则B到平面α的距离为|BO|=.基础自测1.已知a=(λ+1,0,2),b=(6,2μ-1,2λ),若a∥b,则λ与μ的值可以是()A.2,B.-,C.-3,2D.2,2【解析】 a∥b,∴b=ka,即(6,2μ-1,2λ)=k(λ+1,0,2),∴解得或【答案】A2.设u=(-2,2,t),v=(6,-4,4)分别是平面α,β的法向量.若α⊥β,则t=()A.3B.4C.5D.6【解析】 α⊥β,则u·v=-2×6+2×(-4)+4t=0,∴t=5.【答案】C3.已知两平面的法向量分别为m=(0,1,0),n=(0,1,1),则两平面所成的二面角为()3A.45°B.135°C.45°或135°D.90°【解析】cos〈m,n〉===,∴〈m,n〉=45°,其补角为135°.∴两平面所成二面角为45°或135°.【答案】C考点一利用空间向量求线线角、线面角例(2013·湖南高考)图7-7-5如图7-7-5,在直棱柱ABCD-A1B1C1D1中,AD∥BC,∠BAD=90°,AC⊥BD,BC=1,AD=AA1=3.(1)证明:AC⊥B1D;(2)求直线B1C1与平面ACD1所成角的正弦值.【思路点拨】(1)以点A为坐标原点建立空间直角坐标系,用向量法证明线线垂直.(2)...