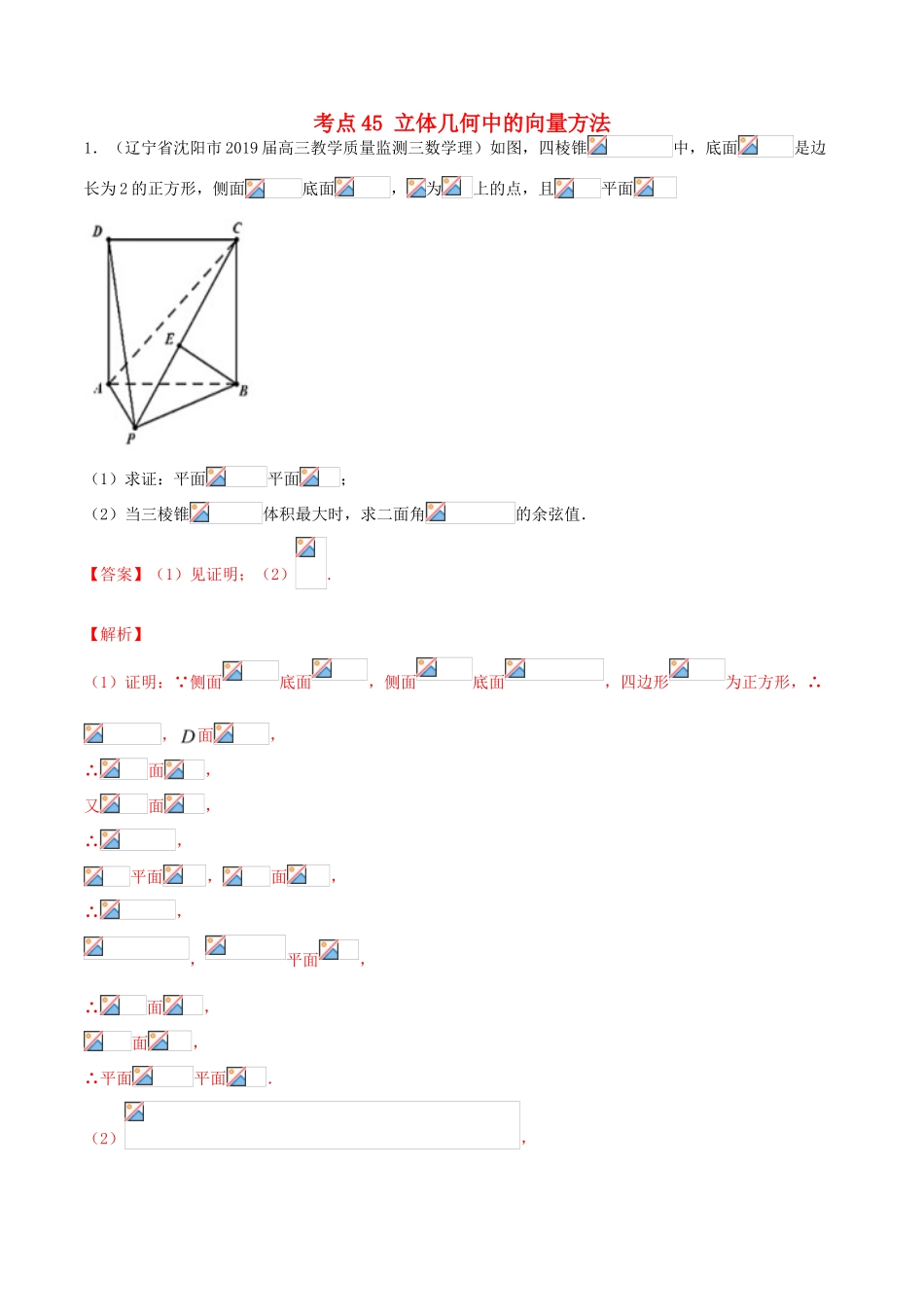
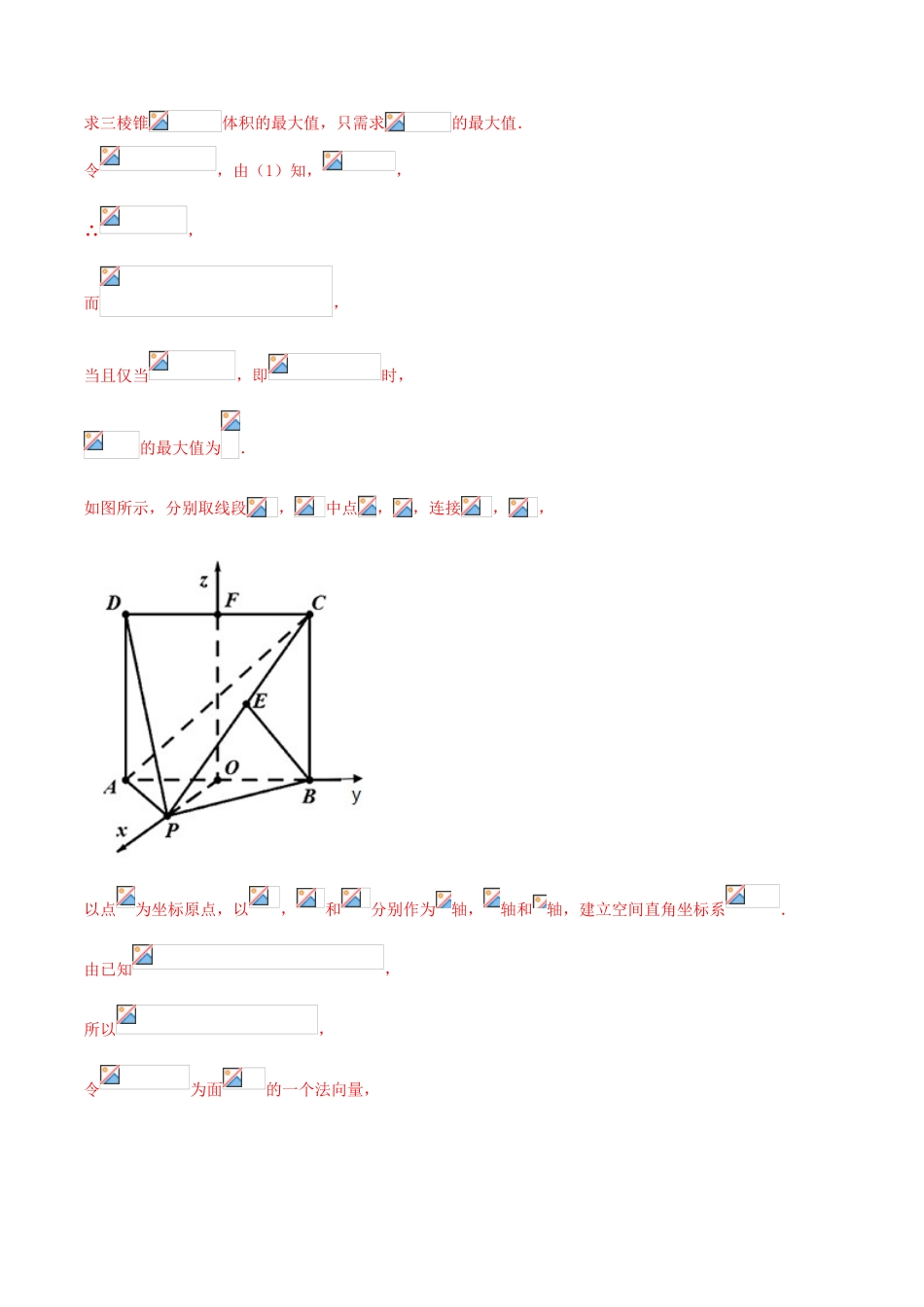
考点45立体几何中的向量方法1.(辽宁省沈阳市2019届高三教学质量监测三数学理)如图,四棱锥中,底面是边长为2的正方形,侧面底面,为上的点,且平面(1)求证:平面平面;(2)当三棱锥体积最大时,求二面角的余弦值.【答案】(1)见证明;(2).【解析】(1)证明: 侧面底面,侧面底面,四边形为正方形,∴,面,∴面,又面,∴,平面,面,∴,,平面,∴面,面,∴平面平面.(2),求三棱锥体积的最大值,只需求的最大值.令,由(1)知,,∴,而,当且仅当,即时,的最大值为.如图所示,分别取线段,中点,,连接,,以点为坐标原点,以,和分别作为轴,轴和轴,建立空间直角坐标系.由已知,所以,令为面的一个法向量,则有,∴易知为面的一个法向量,二面角的平面角为,为锐角则.2.(湖南省长沙市第一中学2019届高三下学期高考模拟卷一数学理)如图所示,圆O的直径AB=6,C为圆周上一点,BC=3,平面PAC垂直圆O所在平面,直线PC与圆O所在平面所成角为60°,PA⊥PC.(1)证明:AP⊥平面PBC(2)求二面角P—AB一C的余弦值【答案】(1)见解析.(2).【解析】(1)由已知可知,又平面平面圆,平面平面圆,∴平面,∴,又,,平面,平面,∴平面.(2)法一:过作于,由于平面平面,则平面,则为直线与圆所在平面所成角,所以.过作于,连结,则,故为二面角的平面角.由已知,,在中,,由得,在中,,故,故,即二面角的余弦值为.法二:过作于,则平面,过作交于,以为原点,、、分别为轴、轴、轴建立空间直角坐标系.则,,,,从而,,设平面的法向量,则得,令,从而,而平面的法向量为,故,即二面角的余弦值为.3.(四川省绵阳市2019届高三下学期第三次诊断性考试数学理)如图,在四棱锥中,底面是菱形,且,,,分别为,的中点,且.(1)求证:平面平面;(2)求锐二面角的余弦值.【答案】(1)见解析;(2)【解析】(1)过P作PO⊥AD,垂足为O,连结AO,BO,由∠PAD=120°,得∠PAO=60°,∴在Rt△PAO中,PO=PAsin∠PAO=2sin60°=2×=, ∠BAO=120°,∴∠BAO=60°,AO=AO,∴△PAO≌△BAO,∴BO=PO=, E,F分别是PA,BD的中点,EF=,∴EF是△PBD的中位线,∴PB=2EF=2×=,∴PB2=PO2+BO2,∴PO⊥BO, AD∩BO=O,∴PO⊥平面ABCD,又PO⊂平面PAD,∴平面PAD⊥平面ABCD.(2)以O为原点,OB为x轴,OD为y轴,OP为z轴,建立空间直角坐标系,A(0,1,0),P(0,0,),B(,0,0),D(0,3,0),∴E(0,),F(,),=(0,),=(,,0),易得平面ABCD的一个法向量=(0,0,1),设平面ACE的法向量=(x,y,z),则,取x=1,得=(1,-,1),设锐二面角的平面角的大小为θ,则cosθ=|cos<>|==,∴锐二面角E-AC-D的余弦值为.4.(四川省宜宾市2019届高三第三次诊断性考试数学理)如图,在四棱锥中,,平面,二面角为为中点.(1)求证:;(2)求与平面所成角的余弦值.【答案】(1)证明见解析;(2).【解析】(1)证明:作SA中点F,连接EF E为SD中点∴ ∴∴得平行四边形∴ 平面∴为二面角的平面角∴ ∴∴∴(2)作AB中点O,由(1)知 ∴平面如图建立空间直角坐标系设,则∴设平面SCD的法向量,得令,则 ∴∴∴AB与平面所成角的余弦值为.5.(安徽省黄山市2019届高三毕业班第三次质量检测数学理)如图,在以为顶点的五面体中,面为正方形,,,且二面角与二面角都是.(1)证明:平面;(2)求直线与平面所成角的正弦值.【答案】(1)证明见解析;(2).【解析】(1)面ABEF为正方形又,而,面,面面(2),则由(1)知面平面,过作,垂足为,平面.以为坐标原点,的方向为轴正方向,为单位长度,建立如图所示的空间直角坐标系.由(1)知为二面角的平面角,故,又,则,,,,.由已知,,平面.又平面平面,故,.由,可得平面,为二面角的平面角,..,,.设是平面的法向量,则,即,可取.则.直线与平面BCE所成角的正弦值为.6.(湖南省师范大学附属中学2019届高三考前演练(五)数学(理)在五边形AEBCD中,,C,,,(如图).将△ABE沿AB折起,使平面ABE⊥平面ABCD,线段AB的中点为O(如图).(1)求证:平面ABE⊥平面DOE;(2)求平面EAB与平面ECD...