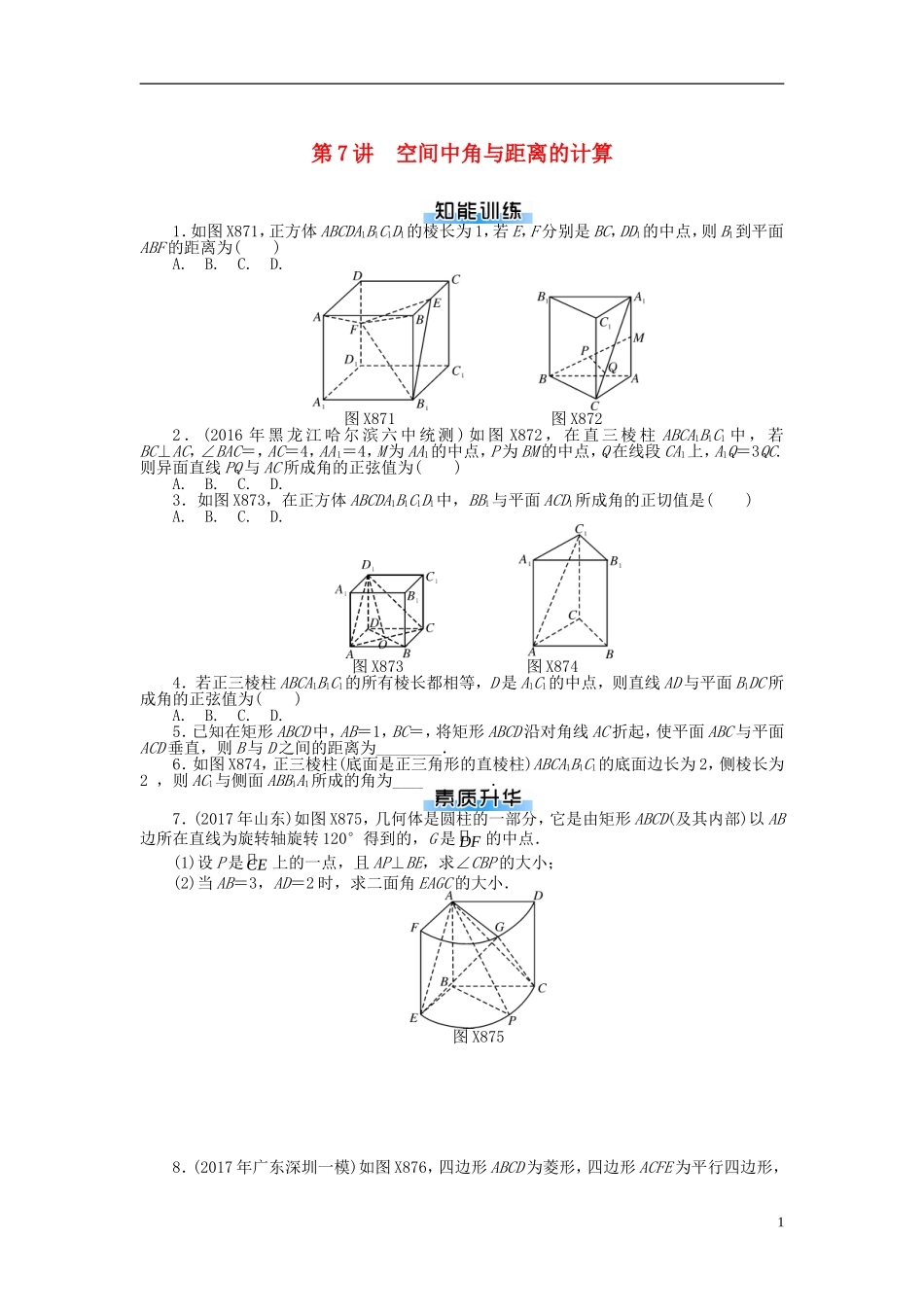
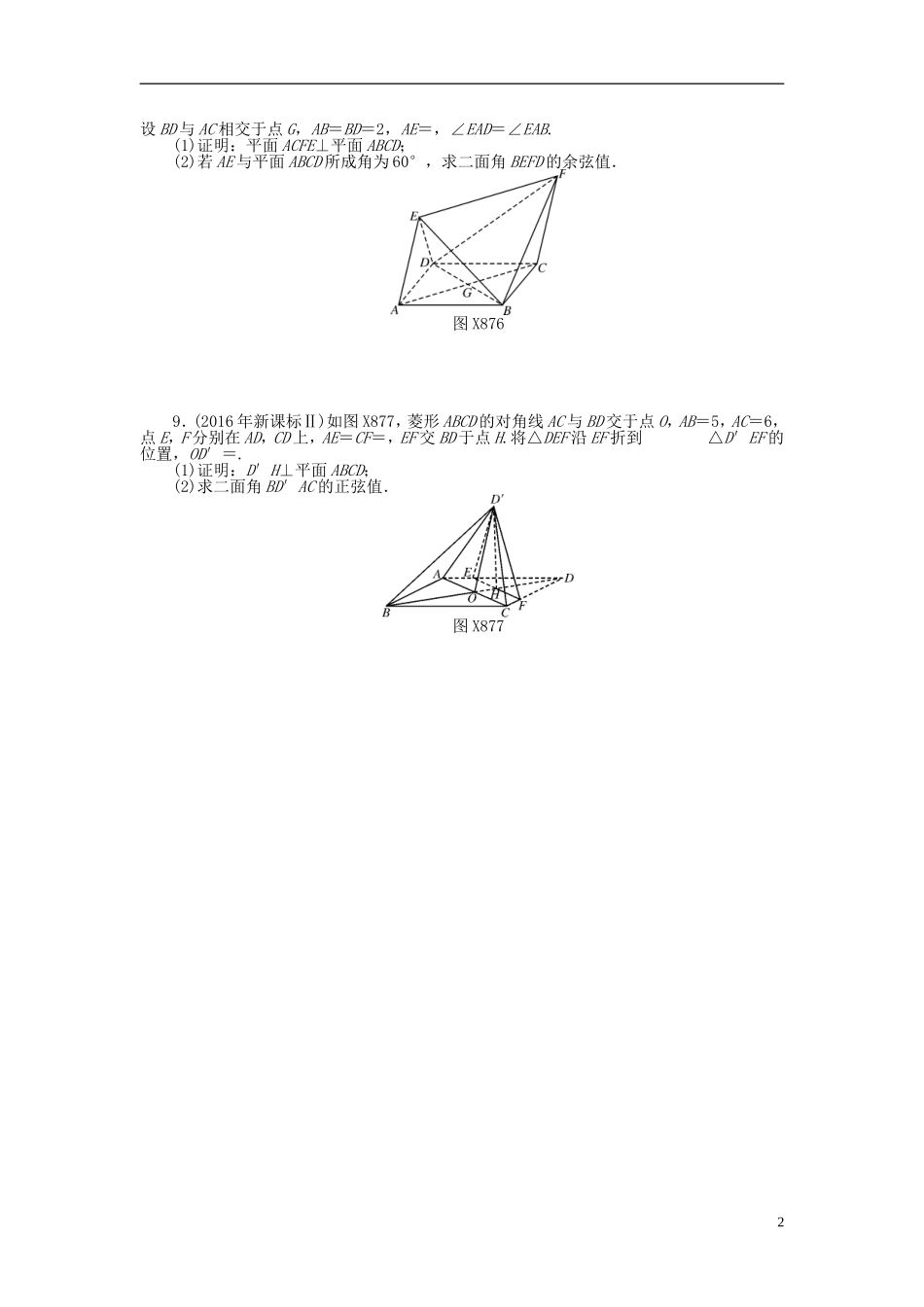
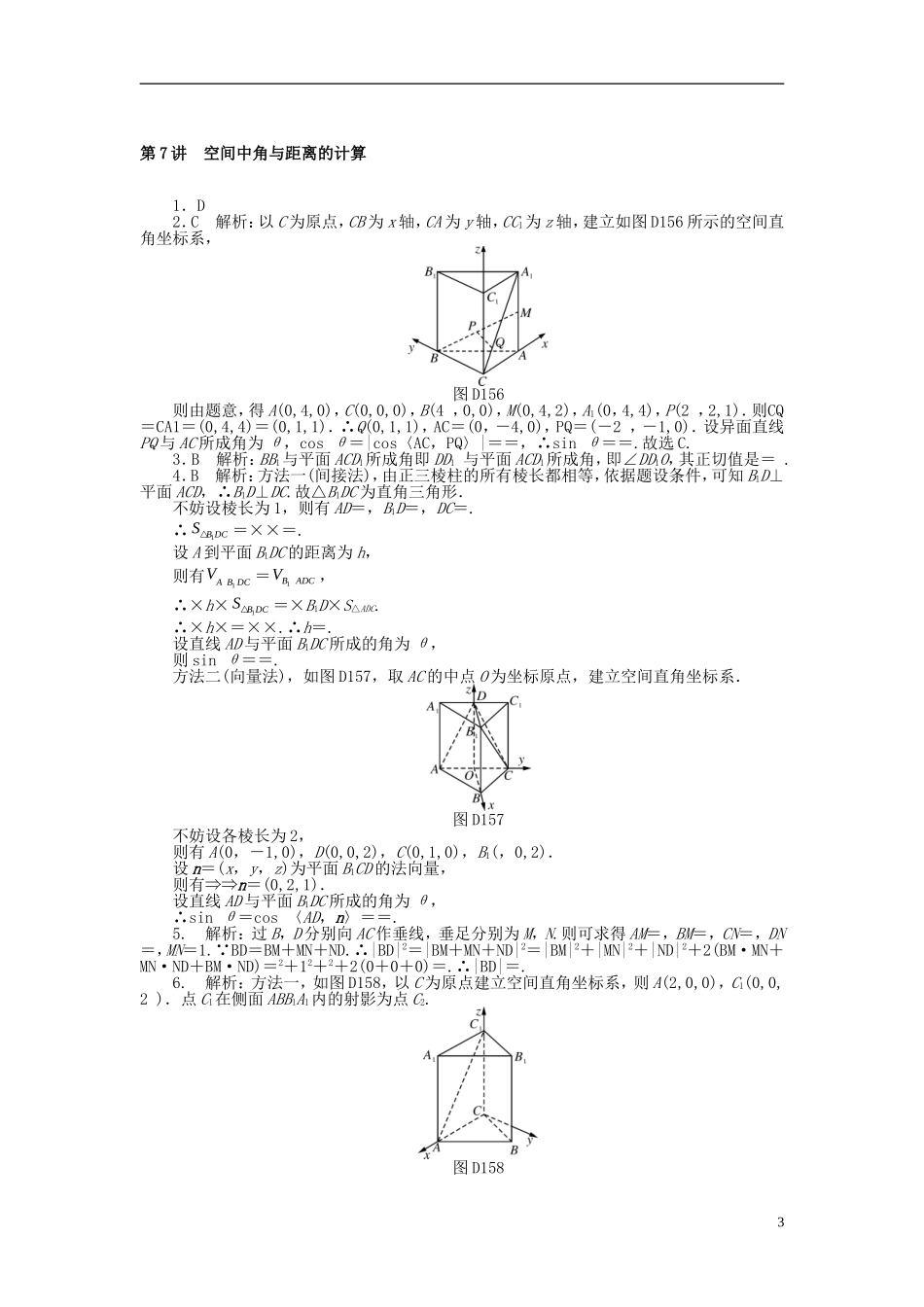
第7讲空间中角与距离的计算1.如图X871,正方体ABCDA1B1C1D1的棱长为1,若E,F分别是BC,DD1的中点,则B1到平面ABF的距离为()A.B.C.D.图X871图X8722.(2016年黑龙江哈尔滨六中统测)如图X872,在直三棱柱ABCA1B1C1中,若BC⊥AC,∠BAC=,AC=4,AA1=4,M为AA1的中点,P为BM的中点,Q在线段CA1上,A1Q=3QC.则异面直线PQ与AC所成角的正弦值为()A.B.C.D.3.如图X873,在正方体ABCDA1B1C1D1中,BB1与平面ACD1所成角的正切值是()A.B.C.D.图X873图X8744.若正三棱柱ABCA1B1C1的所有棱长都相等,D是A1C1的中点,则直线AD与平面B1DC所成角的正弦值为()A.B.C.D.5.已知在矩形ABCD中,AB=1,BC=,将矩形ABCD沿对角线AC折起,使平面ABC与平面ACD垂直,则B与D之间的距离为________.6.如图X874,正三棱柱(底面是正三角形的直棱柱)ABCA1B1C1的底面边长为2,侧棱长为2,则AC1与侧面ABB1A1所成的角为____________.7.(2017年山东)如图X875,几何体是圆柱的一部分,它是由矩形ABCD(及其内部)以AB边所在直线为旋转轴旋转120°得到的,G是DF的中点.(1)设P是CE上的一点,且AP⊥BE,求∠CBP的大小;(2)当AB=3,AD=2时,求二面角EAGC的大小.图X8758.(2017年广东深圳一模)如图X876,四边形ABCD为菱形,四边形ACFE为平行四边形,1设BD与AC相交于点G,AB=BD=2,AE=,∠EAD=∠EAB.(1)证明:平面ACFE⊥平面ABCD;(2)若AE与平面ABCD所成角为60°,求二面角BEFD的余弦值.图X8769.(2016年新课标Ⅱ)如图X877,菱形ABCD的对角线AC与BD交于点O,AB=5,AC=6,点E,F分别在AD,CD上,AE=CF=,EF交BD于点H.将△DEF沿EF折到△D′EF的位置,OD′=.(1)证明:D′H⊥平面ABCD;(2)求二面角BD′AC的正弦值.图X8772第7讲空间中角与距离的计算1.D2.C解析:以C为原点,CB为x轴,CA为y轴,CC1为z轴,建立如图D156所示的空间直角坐标系,图D156则由题意,得A(0,4,0),C(0,0,0),B(4,0,0),M(0,4,2),A1(0,4,4),P(2,2,1).则CQ=CA1=(0,4,4)=(0,1,1).∴Q(0,1,1),AC=(0,-4,0),PQ=(-2,-1,0).设异面直线PQ与AC所成角为θ,cosθ=|cos〈AC,PQ〉|==,∴sinθ==.故选C.3.B解析:BB1与平面ACD1所成角即DD1与平面ACD1所成角,即∠DD1O,其正切值是=.4.B解析:方法一(间接法),由正三棱柱的所有棱长都相等,依据题设条件,可知B1D⊥平面ACD,∴B1D⊥DC.故△B1DC为直角三角形.不妨设棱长为1,则有AD=,B1D=,DC=.∴1BDCS=××=.设A到平面B1DC的距离为h,则有1ABDCV=1BADCV,∴×h×1BDCS=×B1D×S△ADC.∴×h×=××.∴h=.设直线AD与平面B1DC所成的角为θ,则sinθ==.方法二(向量法),如图D157,取AC的中点O为坐标原点,建立空间直角坐标系.图D157不妨设各棱长为2,则有A(0,-1,0),D(0,0,2),C(0,1,0),B1(,0,2).设n=(x,y,z)为平面B1CD的法向量,则有⇒⇒n=(0,2,1).设直线AD与平面B1DC所成的角为θ,∴sinθ=cos〈AD,n〉==.5.解析:过B,D分别向AC作垂线,垂足分别为M,N.则可求得AM=,BM=,CN=,DN=,MN=1. BD=BM+MN+ND.∴|BD|2=|BM+MN+ND|2=|BM|2+|MN|2+|ND|2+2(BM·MN+MN·ND+BM·ND)=2+12+2+2(0+0+0)=.∴|BD|=.6.解析:方法一,如图D158,以C为原点建立空间直角坐标系,则A(2,0,0),C1(0,0,2).点C1在侧面ABB1A1内的射影为点C2.图D1583∴AC1=(-2,0,2),AC2=.设直线AC1与平面ABB1A1所成的角为θ,则cosθ===.又θ∈,所以θ=.方法二,取A1B1的中点H,连接AH,由题意易知C1H⊥平面ABB1A1,∴∠C1AH即为AC1与平面ABB1A1所成的角.在Rt△C1HA中,C1H=,C1A==2,∴∠C1AH=,即AC1与侧面ABB1A所成角为.7.解:(1)因为AP⊥BE,AB⊥BE,又AB,AP⊂平面ABP,AB∩AP=A,所以BE⊥平面ABP.又BP⊂平面ABP,所以BE⊥BP.又∠EBC=120°,所以∠CBP=30°.(2)方法一,取EC的中点H,连接EH,GH,CH,如图D159.因为∠EBC=120°,所以四边形为BEHC为菱形.所以AE=GE=AC=GC==.取AG中点M,连接EM,CM,EC.则EM⊥AG,CM⊥AG.所以∠EMC为所求二面角的平面角.又AM=1,所以EM=CM==2.在△BEC中,由于∠EBC=120°,...