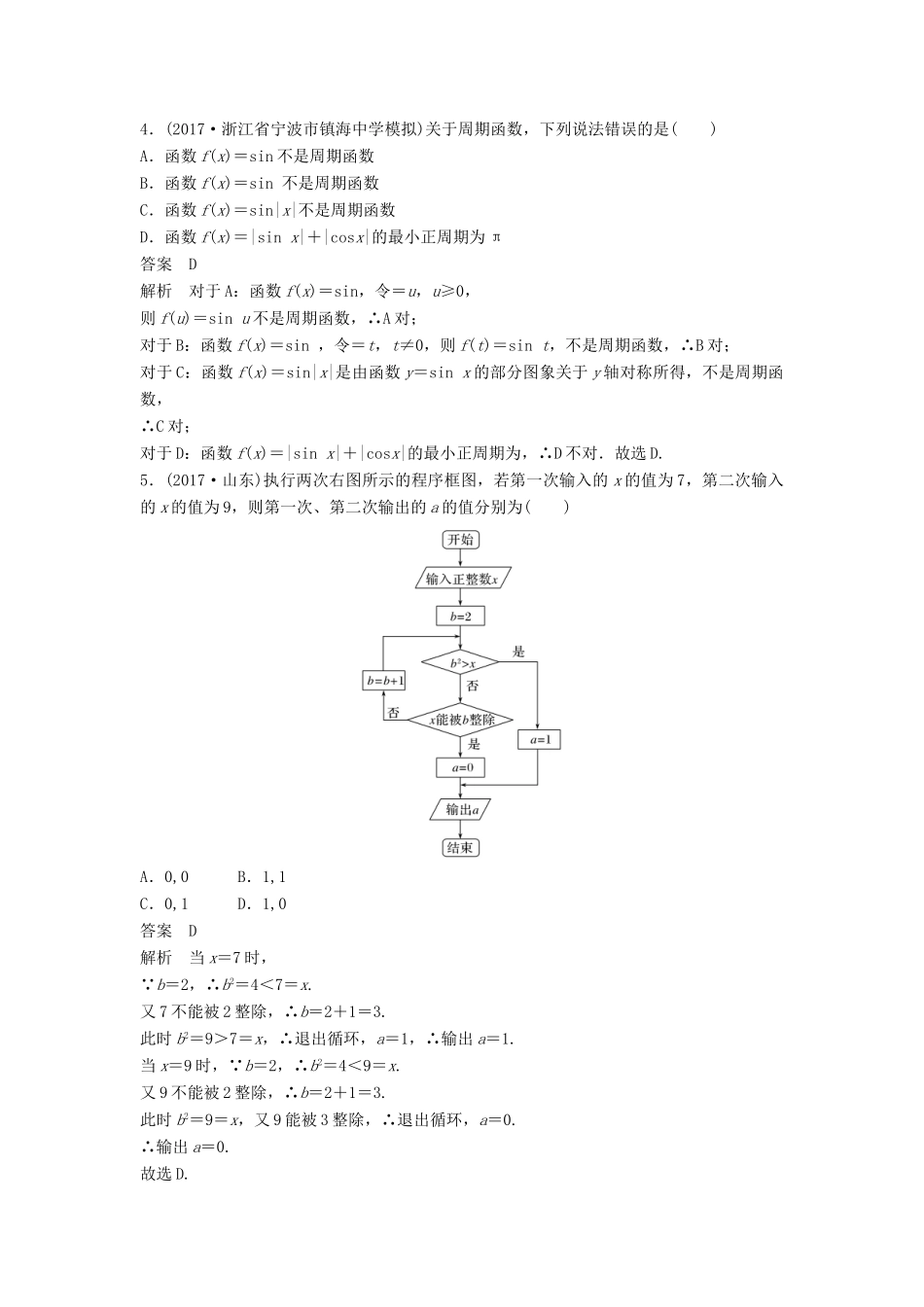
12+4“80分”标准练21.已知集合A={x|(x-1)(x-3)(x-5)<0},B={x∈N|-2<x<6},则A∩B的元素的个数为()A.1B.2C.3D.4答案B解析A={x|(x-1)(x-3)(x-5)<0}={x|3<x<5或x<1},B={x∈N|-2<x<6}={0,1,2,3,4,5},则A∩B={0,4},即A∩B的元素的个数为2,故选B.2.(2017·全国Ⅲ)设复数z满足(1+i)z=2i,则|z|等于()A.B.C.D.2答案C解析方法一由(1+i)z=2i,得z==1+i,∴|z|=.故选C.方法二 2i=(1+i)2,∴由(1+i)z=2i=(1+i)2,得z=1+i,∴|z|=.故选C.3.(2017届山东省、湖北省部分重点中学模拟)为了解决低收入家庭的住房问题,某城市修建了首批216套住房,已知A,B,C三个社区分别有低收入家庭720户,540户,360户,现采用分层抽样的方法决定各社区所分配首批经济住房的户数,则应从C社区抽取低收入家庭的户数为()A.48B.36C.24D.18答案A解析根据分层抽样的要求可知,在C社区抽取户数为216×=216×=48.故选A.4.(2017·浙江省宁波市镇海中学模拟)关于周期函数,下列说法错误的是()A.函数f(x)=sin不是周期函数B.函数f(x)=sin不是周期函数C.函数f(x)=sin|x|不是周期函数D.函数f(x)=|sinx|+|cosx|的最小正周期为π答案D解析对于A:函数f(x)=sin,令=u,u≥0,则f(u)=sinu不是周期函数,∴A对;对于B:函数f(x)=sin,令=t,t≠0,则f(t)=sint,不是周期函数,∴B对;对于C:函数f(x)=sin|x|是由函数y=sinx的部分图象关于y轴对称所得,不是周期函数,∴C对;对于D:函数f(x)=|sinx|+|cosx|的最小正周期为,∴D不对.故选D.5.(2017·山东)执行两次右图所示的程序框图,若第一次输入的x的值为7,第二次输入的x的值为9,则第一次、第二次输出的a的值分别为()A.0,0B.1,1C.0,1D.1,0答案D解析当x=7时, b=2,∴b2=4<7=x.又7不能被2整除,∴b=2+1=3.此时b2=9>7=x,∴退出循环,a=1,∴输出a=1.当x=9时, b=2,∴b2=4<9=x.又9不能被2整除,∴b=2+1=3.此时b2=9=x,又9能被3整除,∴退出循环,a=0.∴输出a=0.故选D.6.(2017·湖北省黄冈中学模拟)设m,n是空间两条直线,α,β是空间两个平面,则下列命题中不正确的是()A.当n⊥α时,“n⊥β”是“α∥β”的充要条件B.当m⊂α时,“m⊥β”是“α⊥β”的充分不必要条件C.当m⊂α时,“n∥α”是“m∥n”的必要不充分条件D.当m⊂α时,“n⊥α”是“m⊥n”的充分不必要条件答案C解析C中,当m⊂α时,若n∥α,则直线m,n可能平行,可能异面;若m∥n,则n∥α或n⊂α,所以“n∥α”是“m∥n”的既不充分也不必要条件,故C项不正确.7.(2017届山东省聊城市三模)已知两点A(-m,0)和B(2+m,0)(m>0),若在直线l:x+y-9=0上存在点P,使得PA⊥PB,则实数m的取值范围是()A.(0,3)B.(0,4)C.[3,+∞)D.[4,+∞)答案C解析以AB为直径的圆的方程为(x-1)2+y2=(1+m)2.在直线l:x+y-9=0上存在点P,使得PA⊥PB,则直线l与圆有公共点.∴≤1+m,解得m≥3.故选C.8.(2016·全国Ⅲ)如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为()A.18+36B.54+18C.90D.81答案B解析由题意知,几何体为平行六面体,边长分别为3,3,,几何体的表面积S=3×6×2+3×3×2+3××2=54+18.9.(2017届山东师大附中模拟)已知双曲线C:-=1(a>0,b>0)右支上非顶点的一点A关于原点O的对称点为B,F为其右焦点,若AF⊥FB,设∠ABF=θ且θ∈,则双曲线离心率的取值范围是()A.(,2]B.(1,]C.(,+∞)D.(2,+∞)答案C解析如图所示,设双曲线的左焦点为F′,连接AF′,BF′. AF⊥FB,∴四边形AFBF′为矩形,因此|AB|=|FF′|=2c,则|AF|=2csinθ,|BF|=2ccosθ. |AF′|-|AF|=2a.∴2ccosθ-2csinθ=2a.即c(cosθ-sinθ)=a,则e===, θ∈,∴θ+∈,则cos∈,cos∈,则>=,即e>,故双曲线离心率的取值范围是(,+∞),故选C.10.(2017届四川省成都市三诊)设等差数列{an}的前n项和为Sn,Sm-1=13,Sm=0,Sm+1=-15.其中m∈N*且m≥2,则数列的前n项和的最大值为()A.B.C.D.答案D解析 Sm-1=13,Sm=0,S...