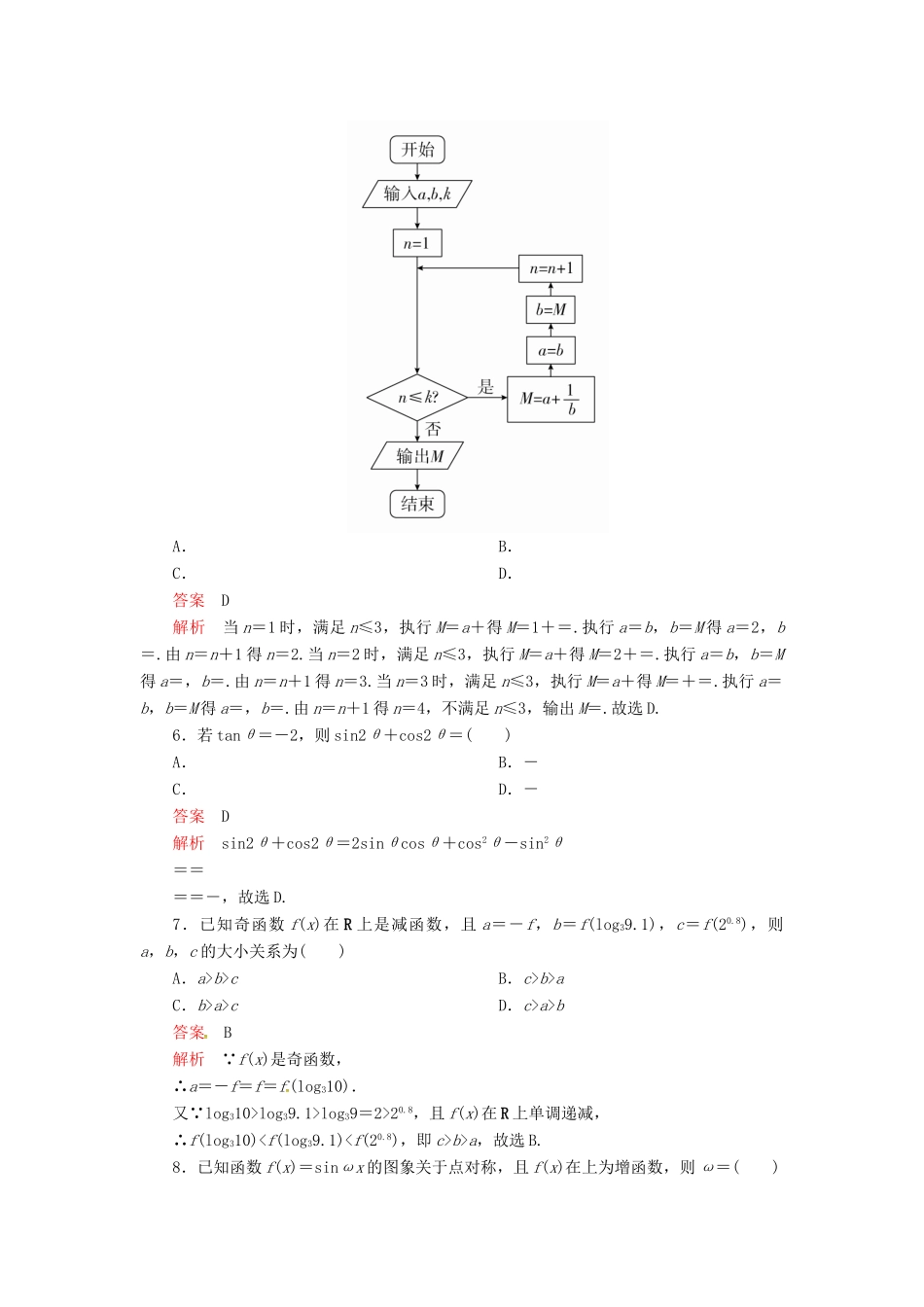
三基保分强化训练(七)1.已知集合A={x|x(x-1)<0},B={x|ex>1},则(∁RA)∩B=()A.[1,+∞)B.(0,+∞)C.(0,1)D.[0,1]答案A解析A=(0,1),B=(0,+∞),∁RA=(-∞,0]∪[1,+∞),(∁RA)∩B=[1,+∞).2.已知复数z=为纯虚数,则a=()A.1B.C.2D.-2答案B解析z===,由z为纯虚数,得2a-1=0且a+2≠0,∴a=,故选B.3.80名学生的高中数学竞赛成绩(单位:分)的频率分布直方图如图所示,则成绩落在[50,70)中的学生人数为()A.25B.20C.15D.10答案B解析根据频率分布直方图知组距为10,由(2a+3a+7a+6a+2a)×10=1,解得a==0.005.则成绩落在[50,70)中的学生人数为(2×0.005×10+3×0.005×10)×80=20.故选B.4.在区间[1,4]上任取两个实数,则所取两个实数之和大于3的概率为()A.B.C.D.答案D解析依题意,记从区间[1,4]上取出的两个实数为x,y,不等式组表示的平面区域的面积为(4-1)2=9,不等式组表示的平面区域的面积为(4-1)2-×12=,因此所求的概率为=,选D.5.执行如图所示的程序框图,若输入的a,b,k分别为1,2,3,则输出的M=()A.B.C.D.答案D解析当n=1时,满足n≤3,执行M=a+得M=1+=.执行a=b,b=M得a=2,b=.由n=n+1得n=2.当n=2时,满足n≤3,执行M=a+得M=2+=.执行a=b,b=M得a=,b=.由n=n+1得n=3.当n=3时,满足n≤3,执行M=a+得M=+=.执行a=b,b=M得a=,b=.由n=n+1得n=4,不满足n≤3,输出M=.故选D.6.若tanθ=-2,则sin2θ+cos2θ=()A.B.-C.D.-答案D解析sin2θ+cos2θ=2sinθcosθ+cos2θ-sin2θ====-,故选D.7.已知奇函数f(x)在R上是减函数,且a=-f,b=f(log39.1),c=f(20.8),则a,b,c的大小关系为()A.a>b>cB.c>b>aC.b>a>cD.c>a>b答案B解析∵f(x)是奇函数,∴a=-f=f=f(log310).又∵log310>log39.1>log39=2>20.8,且f(x)在R上单调递减,∴f(log310)
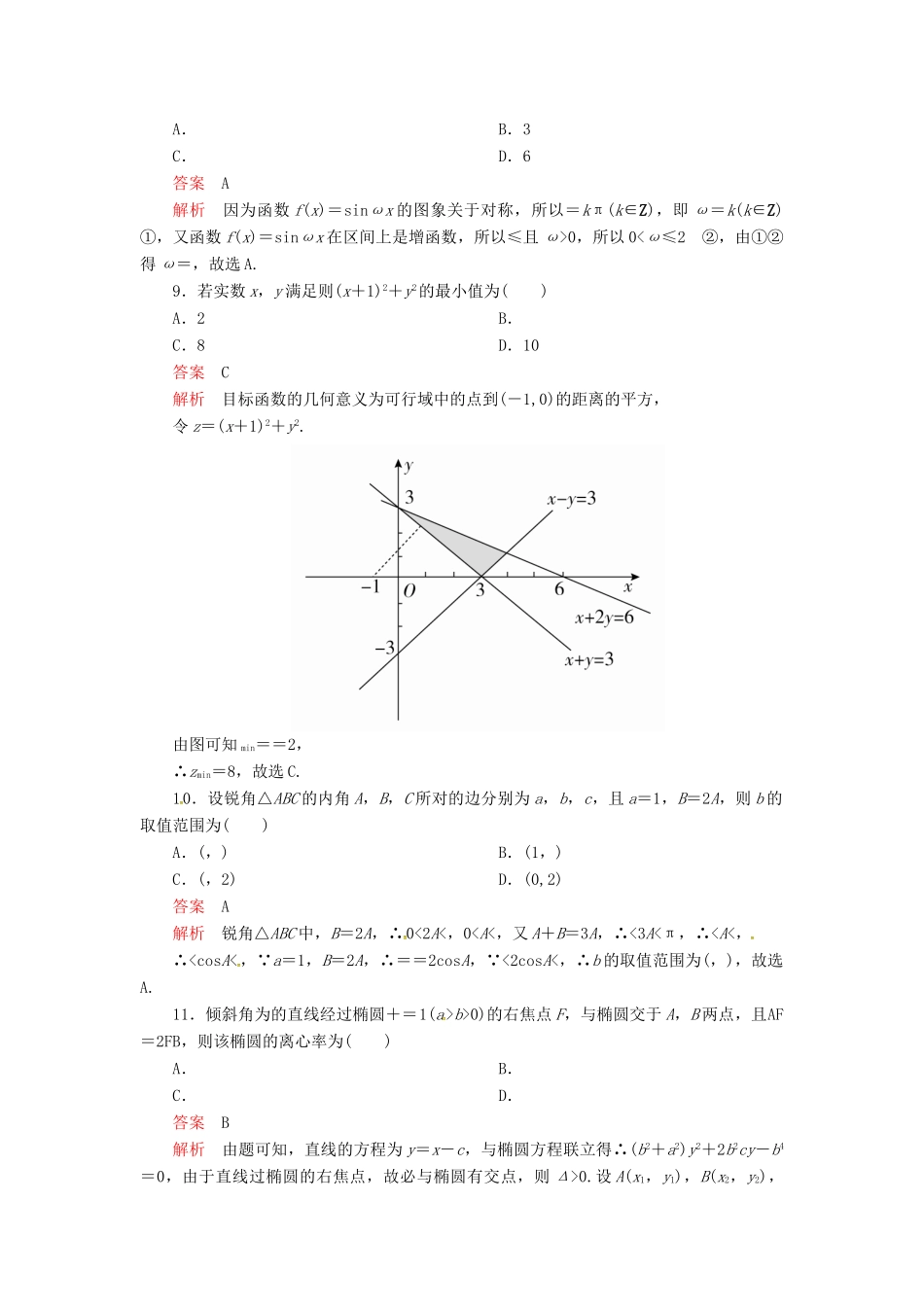
b>a,故选B.8.已知函数f(x)=sinωx的图象关于点对称,且f(x)在上为增函数,则ω=()A.B.3C.D.6答案A解析因为函数f(x)=sinωx的图象关于对称,所以=kπ(k∈Z),即ω=k(k∈Z)①,又函数f(x)=sinωx在区间上是增函数,所以≤且ω>0,所以0<ω≤2②,由①②得ω=,故选A.9.若实数x,y满足则(x+1)2+y2的最小值为()A.2B.C.8D.10答案C解析目标函数的几何意义为可行域中的点到(-1,0)的距离的平方,令z=(x+1)2+y2.由图可知min==2,∴zmin=8,故选C.10.设锐角△ABC的内角A,B,C所对的边分别为a,b,c,且a=1,B=2A,则b的取值范围为()A.(,)B.(1,)C.(,2)D.(0,2)答案A解析锐角△ABC中,B=2A,∴0<2A<,0b>0)的右焦点F,与椭圆交于A,B两点,且AF=2FB,则该椭圆的离心率为()A.B.C.D.答案B解析由题可知,直线的方程为y=x-c,与椭圆方程联立得∴(b2+a2)y2+2b2cy-b4=0,由于直线过椭圆的右焦点,故必与椭圆有交点,则Δ>0.设A(x1,y1),B(x2,y2),则又AF=2FB,∴(c-x1,-y1)=2(x2-c,y2),∴-y1=2y2,可得∴=,∴e=,故选B.12.已知向量a,b的夹角为,且a·(a-b)=1,|a|=2,则|b|=________.答案3解析∵a·(a-b)=a·a-a·b=|a|2-|a|·|b|·cos=4-|b|=1,∴|b|=3.13.已知x,y满足不等式组则z=的取值范围为________.答案解析可行域为如图所示的阴影部分,由图可知,x>0,y>0,所以目标函数z=可化为=,记u=,则u=表示可行域内的点与点P(-2,0)连线的斜率,由得所以B(1,2),由得所以C,所以kPB==,kPC==.根据图形可以看出,kPB≤u≤kPC,所以≤u≤,所以≤z≤,即z=的取值范围为.14.若数列{an}是正项数列,且++…+=n2+2n(n∈N*),则++…+=________.答案120解析记Tn=++…+,∴=Tn-Tn-1=n2+2n-[(n-1)2+2(n-1)]=2n+1,∴an=(2n+1)2(n≥2),令n=1,∴=3⇒a1=9,∴an=(2n+1)2,∴=2n+1,∴++…+=2(1+2+3+…+n)+n=n2+2n,∴++…+=120,故答案为120.