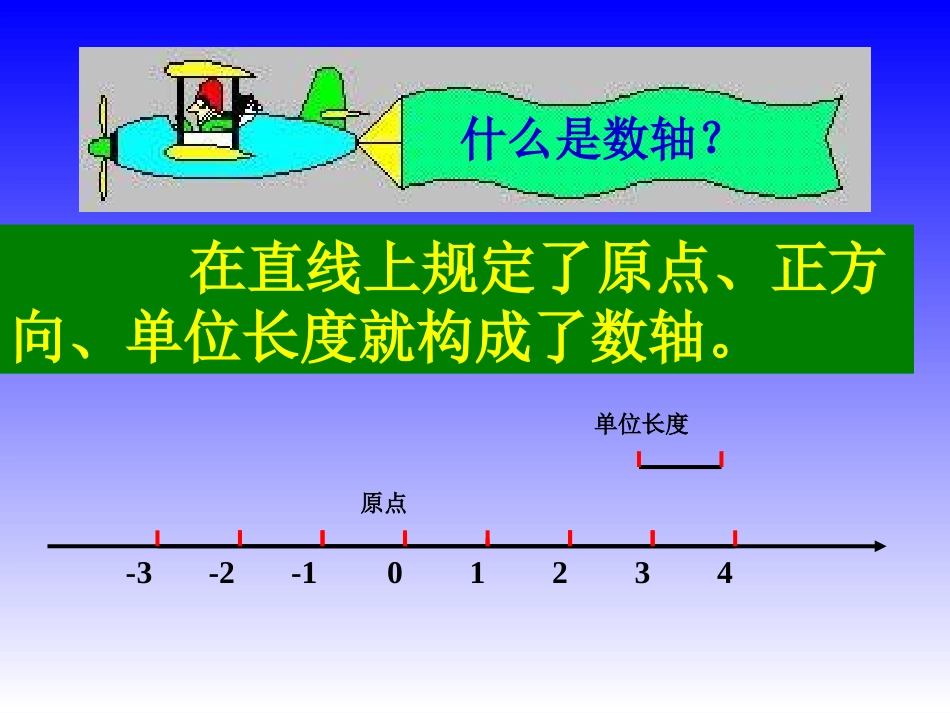
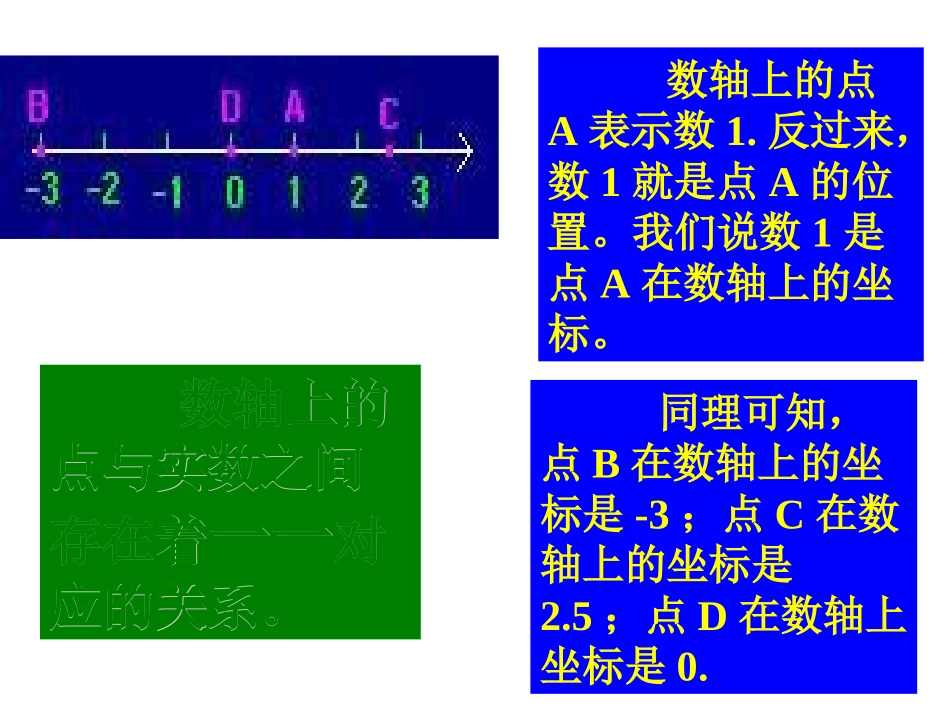
如何确定直线上点的位置?在直线上规定了原点、正方向、单位长度就构成了数轴。数轴上的点可以用一个数来表示,这个数叫做这个点在数轴上的坐标.例如点A在数轴上的坐标为-3,点B在数轴上的坐标为2。反过来,知道数轴上一个点的坐标,这个的点在数轴上的位置也就确定了。·单位长度01234-3-2-1原点••AB什么是数轴?在直线上规定了原点、正方向、单位长度就构成了数轴。单位长度01234-3-2-1原点数轴上的点A表示数1.反过来,数1就是点A的位置。我们说数1是点A在数轴上的坐标。同理可知,点B在数轴上的坐标是-3;点C在数轴上的坐标是2.5;点D在数轴上坐标是0.数轴上的数轴上的点与实数之间点与实数之间存在着存在着一一一一对对应的关系应的关系。。类似于用数轴确定直线上点的位置,能否找到一种办法来确定平面内的点的位置呢?(例如下图中A、B、C、D各点)当然有办法了,法国数学家笛卡儿就想出了办法,你们看——早在1637年以前,法国数学家、解析几何的创始人笛卡尔受到了经纬度的启发,地理上的经纬度是以赤道和本初子午线为标准的,这两条线从局部上可以看成是平面内互相垂直的两条直线。所以笛卡尔的方法是在平面内画两条互相垂直的数轴,其中水平的数轴叫x轴(或横轴),取向右为正方向,铅直的数轴叫y轴(或纵轴),取向上为正方向,它们的交点是原点,这个平面叫坐标平面。这节课我们来学习平面直角坐标系。如何用一对数来表示平面内的点的位置呢?讲台刘明·m(4,6)列行123462841050①两条数轴②互相垂直③公共原点叫平面直角坐标系笛卡儿如上图,我们可以在平面内画两条互相垂直、原点重合的数轴,这就组成了笛卡儿发明的平面直角坐标系。水平的数轴称为X轴或横轴,习惯上取向右为正方向;竖直的数轴的数轴称为y轴或纵轴,取向上方向为正方向;两坐标轴的交点为平面直角坐标系的原点原点X轴y轴有了平面直角坐标系,平面内的一个点就可以用一个有序数对来表示了。例如,如左图,点点A分别向x轴和y轴作垂线,垂足M在x轴上的坐标是3,垂足N在y轴上的坐标是4,我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作(3,4)。那么类似地,请你写出点B、C、D的坐标好吗?B()C()D()想一想:原点O的坐标是什么呢?X轴和y轴上的点的坐标有什么特点?-3,-40,20,-3·A31425-2-4-1-3012345-4-3-2-1x横轴y纵轴A的横坐标为4A的纵坐标为2有序数对(4,2)就叫做A的坐标记作:A(4,2)X轴上的坐标写在前面·BB(-4,1)MN·B31425-2-4-1-3012345-4-3-2-1x横轴y纵轴·C·A·E·D(2,3)(3,2)(-2,1)(-4,-3)(1,-2)坐标是有序数对。例1、写出图中A、B、C、D、E各点的坐标。5-5-2-3-4-13241-66y-55-3-44-23-121-66oXx轴或横轴y轴或纵轴原点平面直角坐标系第一象限第二象限第三象限第四象限注意:坐标轴上的点不属于任何象限。根据点所在位置,用“+”“-”或“0”添表点的位置横坐标符号纵坐标符号在第一象限++在第二象限在第三象限在第四象限在正半轴上在x轴上在负半轴上在正半轴上在y轴上在负半轴上原点----+++00--00+00掌握x轴,y轴上点的坐标的特点:x轴上的点的纵坐标为0,表示为(x,0)y轴上的点的横坐标为0,表示为(0,y)例:在平面直角坐标系中描出下列各点:A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4)可以先在x轴上找出表示4的点,再在y轴上找出表示5的点,地这两个点分别作x轴和y轴的垂线,垂线的交点就是点A。类似地,我们可以在坐标系中也描出点B、C、D、E。A(4,5)O11(-3,4)(-5,-2)(3,-2)(5,4)ACBDA与D、B与C的纵坐标相同吗?为什么?A与B,C与D的横坐标相同吗?为什么?xy写出平行四边形ABCD各个顶点的坐标。平行于横轴的直线上的点的纵坐标相同;平行于纵轴的直线上的点的横坐标相同;横轴上的点纵坐标为0;纵轴上的点横坐标为0。