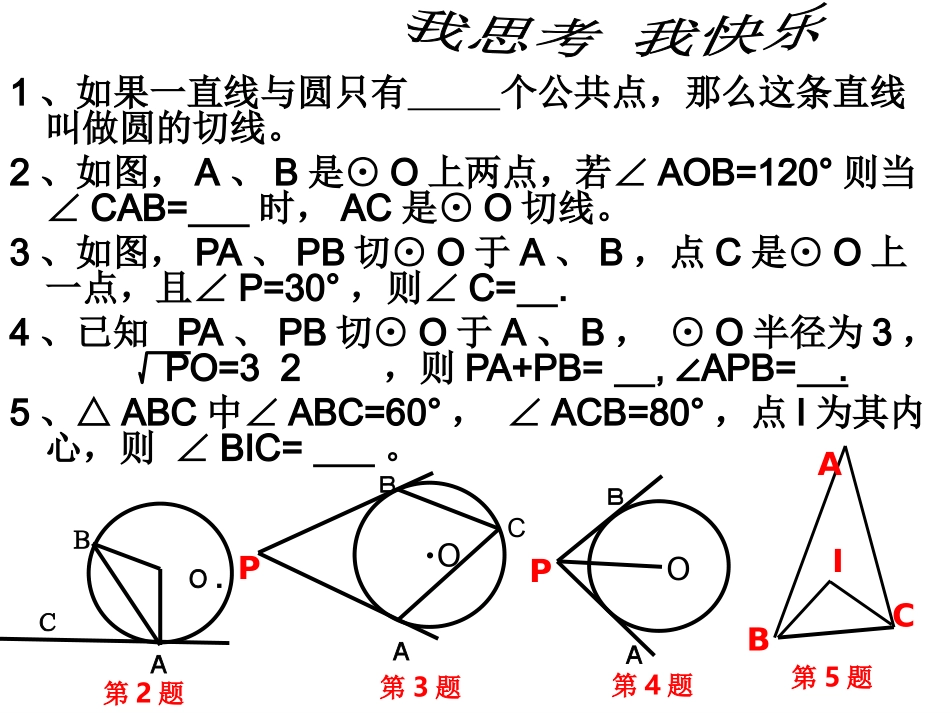
上港乡一初中陶景川1、如果一直线与圆只有个公共点,那么这条直线叫做圆的切线。2、如图,A、B是⊙O上两点,若∠AOB=120°则当∠CAB=时,AC是⊙O切线。3、如图,PA、PB切⊙O于A、B,点C是⊙O上一点,且∠P=30°,则∠C=.4、已知PA、PB切⊙O于A、B,⊙O半径为3,PO=32,则PA+PB=,APB=∠.5、△ABC中∠ABC=60°,∠ACB=80°,点I为其内心,则∠BIC=。ABOPCBO.ABCABCI第2题AOP第3题第4题第5题6、如图,△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,问:⊙O与AC相切吗?说明理由.7.如图:已知PA是⊙O的切线,A为切点,AC是⊙O的直径,BC//OP交⊙O于点B,问:(1)⊙O与PB相切吗?说明理由.展示点评任务工表展示小组展示方式评价小组第1、2、3题第2组口述第4、5题第4组口述第6题第3组板书第7题第1组板书展示要求:1、书写迅速,字迹工整、内容简练,思路清晰,格式规范;2、标明本题知识方法总结。展示点评任务分工评价要求:1.声音洪亮,条理清晰,突出重点,语言简练;2.点评解题方法及思路;3.恰当指出展示成果的优缺点并打分;4.补充或阐述不同观点,或者做变式训练。展示小组展示方式评价小组第1、2、3题第2组口述第3组第4、5题第4组口述第2组第6题第3组板书第5组第7题第1组板书第6组1、如果一直线与圆只有个公共点,那么这条直线叫做圆的切线。2、如图,A、B是⊙O上两点,若∠AOB=120°则当∠CAB=时,AC是⊙O切线。3、如图,PA、PB切⊙O于A、B,点C是⊙O上一点,且∠P=30°,则∠C=.4、已知PA、PB切⊙O于A、B,⊙O半径为3,PO=32,则PA+PB=,APB=∠.5、△ABC中∠ABC=60°,∠ACB=80°,点I为其内心,则∠BIC=。ABOPCBO.ABCABCI第2题AOP第3题第4题第5题知识归纳1、切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线。切线的性质定理:圆的切线垂直于经过切点的半径。2、切线长定理:从圆外一点引圆的两条切线,它们的切线长相等。这一点和圆心的连线平分这两条切线的夹角。3、内心的性质:(1)三角形的内心和三角形顶点的连线平分每个内角;(2)三角形的内心到三角形三边的距离相等。6、如图,△ABC中,AB=AC,O是BC的中点,以O为圆心的⊙O切AB于D,问:⊙O与AC相切吗?说明理由.7.如图:已知PA是⊙O的切线,A为切点,AC是⊙O的直径,BC//OP交⊙O于点B,问:(1)⊙O与PB相切吗?说明理由.∟ME知识归纳1、切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线。切线的性质定理:圆的切线垂直于经过切点的半径。2、切线长定理:从圆外一点引圆的两条切线,它们的切线长相等。这一点和圆心的连线平分这两条切线的夹角。3、内心的性质:(1)三角形的内心和三角形顶点的连线平分每个内角;(2)三角形的内心到三角形三边的距离相等。4、证明切线的方法:(1)定义;(2)d=r法(题中没有明确已知直线与圆有公共点时);(3)判定定理(题中明确已知直线与圆有公共点时)。质疑再探同学们,通过本节的复习,你有什么疑惑请提出来,我们共同解决。3、如图,EF为⊙O外的一条直线,OB为⊙O的半径,OB延长线与EF垂直交于点H,AB的延长线交⊙O于C,过C点作⊙O的切线交EF于点D,试猜想AD=DC是否成立?请说明理由。F运用拓展1、如图,P为⊙O外一点,PA切⊙O于点A,且OP=5,PA=4,则sin∠APO等于()A、B、C、D、2、如图⊙O为△ABC的内切圆,切点分别为D、E、F若AB=15,BC=9,AC=8,则AD=。43—45—35—34—PAOOABCDEF.B7EBCDAOHF4、请结合本节知识自编一道习题,同桌交换解答,好的推荐给老师进行全班交流。课堂小结通过本节课学习,你有什么体会和收获,请谈一谈。