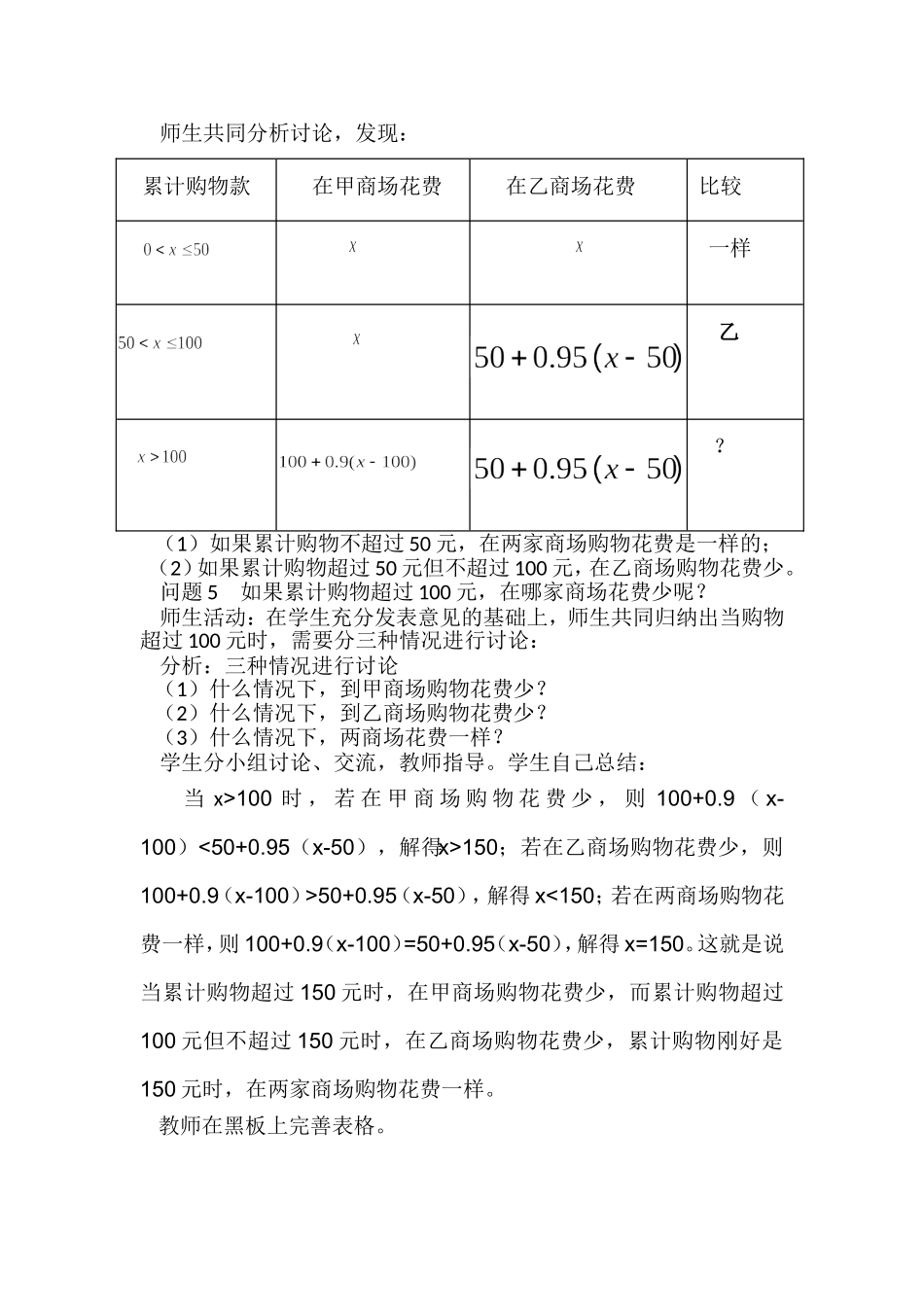
9.2一次一次不等式(第3课时)一、内容和内容解析1.内容利用一元一次不等式解决具有不等关系的实际问题。2.内容解析不等关系和相等关系都是客观世界中量与量之间最基本的数学关系。因此,不等式与方程一样,都是解决数学问题的重要工具,在数学研究和解决实际问题中起着同样重要的作用。本章重点是利用不等式来描述和刻画现实世界的不等关系。本节内容的关键是从实际问题中抽象出数量关系,并通过对数量关系的分析,找出其中的不等关系,引导学生完成抽象过程(从实际问题到数学问题),建立数学模型(列出不等式)进行讨论求解,在将数学问题转化为实际问题进行解答。本节课的教学重点是:分析实际问题中的不等关系列出一元一次不等式。二、目标和目标解析1.目标能从实际问题中抽象出数学问题,根据数量关系建立一元一次不等式进行求解,体会数学建模的思想。2.目标解析达到目标的标志是,学生能够在原有知识的基础上学习建立一元一次不等式的数学模型来解决实际问题。一是抽象,即从实际问题到数学问题,找出数量关系,明确数量中的不等关系;二是建立一元一次不等式的数学模型,把实际问题转化为数学问题进行求解。在此过程中,学生能够继续积累利用一元一次不等式解决实际问题的经验。三、教学问题诊断分析在前面所学的知识中,学生已掌握如何求不等式的解。作为七年级的学生对于用不等关系建立数学模型来解决实际问题,容易出现的认知困难主要是:如何从实际问题出发,抽象出隐含在实际问题中的数量关系,找出数量关系中的不等关系,列一元一次不到能手,需要分类讨论的思想。本节课的教学难点是:如何从实际问题抽象出不等关系,建立不等式模型进行求解。四、教学过程设计教师引出本节课的内容:前面我们结合实际问题,讨论了如何列一元一次不等式,还学习了解一元一次不等式的方法。在本节课上,我们将进一步探究如何用一元一次不等式解决生活中的一些实际问题。在现实生活中我们天天都面临着各种选择,今天我们来讨论生活中最常见的购物问题。1.问题探究甲、乙两商场以同样的价格出售同样的商品,并且又各自推出不同的优惠方案:在甲商场累计购买100元后,超出100元的部分按90%收费;在乙商场累计购买超过50元后,超过50元的部分按95%收费.顾客到哪家商场购物花费少?问题1你是如何理解题意的呢?师生活动:学生先独立思考,理解题意,然后自由发表自己的观点。问题2如果累计购物款为x元,你能用含有x的式子分别表示在两家商场花费的钱数吗?师生活动:学生回答,教师不断引导并完善。问题3你能清楚直观地表示上述问题吗?师生活动:引导学生利用表格表示出来,并让学生在黑板上绘制表格。设累计购物款为x元。问题4你能看出在哪家商场购物花费少呢?师生活动:学生探究、交流,补全表格。累计购物款在甲商场花费在乙商场花费师生共同分析讨论,发现:(1)如果累计购物不超过50元,在两家商场购物花费是一样的;(2)如果累计购物超过50元但不超过100元,在乙商场购物花费少。问题5如果累计购物超过100元,在哪家商场花费少呢?师生活动:在学生充分发表意见的基础上,师生共同归纳出当购物超过100元时,需要分三种情况进行讨论:分析:三种情况进行讨论(1)什么情况下,到甲商场购物花费少?(2)什么情况下,到乙商场购物花费少?(3)什么情况下,两商场花费一样?学生分小组讨论、交流,教师指导。学生自己总结:当x>100时,若在甲商场购物花费少,则100+0.9(x-100)<50+0.95(x-50),解得x>150;若在乙商场购物花费少,则100+0.9(x-100)>50+0.95(x-50),解得x<150;若在两商场购物花费一样,则100+0.9(x-100)=50+0.95(x-50),解得x=150。这就是说当累计购物超过150元时,在甲商场购物花费少,而累计购物超过100元但不超过150元时,在乙商场购物花费少,累计购物刚好是150元时,在两家商场购物花费一样。教师在黑板上完善表格。累计购物款在甲商场花费在乙商场花费比较一样乙?累计购物款在甲商场花费在乙商场花费比较一样乙乙一样甲问题6你能综合上面分析,给出一个合理化的消费方案吗?师生互动:学生回答:购物不超过50元和刚好是150元时,在两家商场购物...