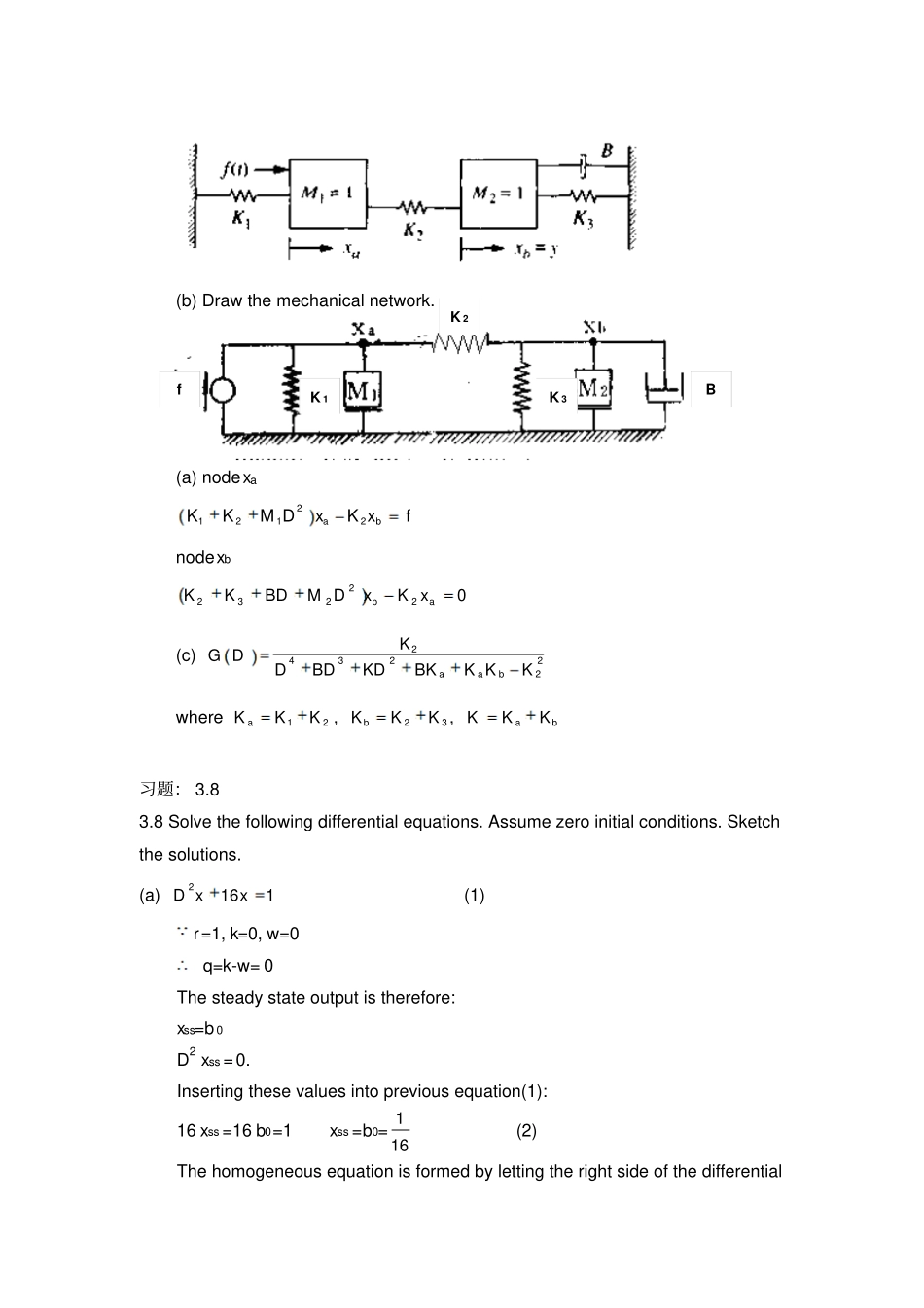
机械控制理论基础习题答案习题:2.2,2.62.2.Writethe(a)loop,(b)nodeequationsforthecircuitshownaftertheswitchSisclosed.2.2.当开关S闭合后,写出电路的(a)回路,(b)节点方程式。(a)loop121111iRiiECDCD221121110iiLDRiCDCDCD(b)nodeNode1betweenR1andR2,Node2betweenR2andL,andNode3betweenLandC21.1212112111110vEvRRCDRR2.2132211110vvvRLDRLD3.232110CDvvLDLD2.6.(a)Derivethedifferentialequationrelatingthepositiony(t)andtheforcef(t).(b)Drawthemechanicalnetwork.(c)DeterminethetransferfunctionG(D)=y/f.2.6.(a)求位置y(t)与力f(t)有关的微分方程;(b)画出机械网络图;(c)确定传递函数G(D)=y/f。123(b)Drawthemechanicalnetwork.(a)nodexa21212abKKMDxKxfnodexb022232abxKxDMBDKK(c)243222aabKGDDBDKDBKKKKwhere12aKKK,23bKKK,abKKK习题:3.83.8Solvethefollowingdifferentialequations.Assumezeroinitialconditions.Sketchthesolutions.(a)1162xxD(1)r=1,k=0,w=0q=k-w=0Thesteadystateoutputistherefore:xss=b0D2xss=0.Insertingthesevaluesintopreviousequation(1):16xss=16b0=1xss=b0=161(2)ThehomogeneousequationisformedbylettingtherightsideofthedifferentialK2BK3K1fequationequalzero:0162ttxxD(3)thetransientresponseisthesolutionofthehomogeneousequation,isobtainedbyassumingasolutionoftheformxt=Amemt(4)wheremisaconstantyettobedeterminedthecharacteristicequationofsystem:01616202mmm(5)m1=4j,m2=-4jvaluesofmarecomplex,byusingtheEuleridentitycossindjtddetjtandthencombiningterms,transientsolutionsare)4sin(4sin4cos214241tAtBtBeAeAxjtjtt(6)x=xt+xss=161)4sin(tA(7)Assumezeroinitialconditions,i.e.,t=0,x(0)=0,Dx(0)=0,insertingthesevaluesintopreviousequation(7):0161sin)0(Ax,0cos4)0(ADx2,161Ax=xt+xss=161)24sin(161t(b)9342xDxxD(1)r=9,k=0,w=0q=k-w=0Thesteadystateoutputistherefore:xss=b0Dxss=0,D2xss=0.Insertingthesevaluesintopreviousequation(1):3xss=9,b0=3xss=b0=3(2)Thehomogeneousequationisformedbylettingtherightsideofthedifferentialequationequalzero:0342xDxxD(3)thetransientresponseisthesolutionofthehomogeneousequation,isobtainedbyassumingasolutionoftheformxt=Amemt(4)wheremisaconstantyettobedeterminedthecharacteristicequationofsystem:0342mm(5)m1=-3,m2=-1Therearenomultipleroots,transientsolutionsarettteAeAx231(6)x=xt+xss=3231tteAeA(7)Assumezeroinitialconditions,i.e.,t=0,x=0,Dx(0)=0,insertingthesevaluesintopreviousequation(7)and(1):03210AAxt0332102310AAeAeADxtttt5.11A,5.42Ax=xt+xss=35.45.13ttee(c)125.42txDxxD(1)r=t+1,k=1,w=0q=k-w=1Thesteadystateoutputistherefore:xss=b1t+b0Dxss=b1,D2xss=0.Insertingthesevaluesintopreviousequation(1):4.25b1t+b1+4.25b0=t+1b1=25.41=0.2353,b0=0.18xss=0.2353t+0.18(2)Thehomogeneousequationisformedbylettingtherightsideofthedifferentialequationequalzero:025.42xDxxD(3)thetransientresponseisthesolutionofthehomogeneousequation,isobtainedbyassumingasolutionoftheformxt=Amemt(4)wheremisaconstantyettobedeterminedthecharacteristicequationofsystem:025.42mm(5)m1=-0.5+j2,m2=-0.5-j2valuesofmarecomplex,byusingtheEuleridentitycossindjtddetjtandthencombiningterms,transientsolutionsare)2sin()(5.022215.0tAeeAeAexttttt(6)x=xt+xss)2sin(2353.018.0)(2353.018.05.022215.0tAeteAeAettttt(7)Assumezeroinitialconditions,i.e.,t=0,x=0,insertingthesevaluesintopreviousequation(7)and(1):0sin18.018.0210AAAxtcos22353.0222353.0210AAADxtsin4442102AAAxDt12353.02621AA1)sin18.0(25.4cos22353.0sin4AAAx=xt+xss=)1322sin(242.02353.018.05.0tett(d)txDxxDxD10sin1024323(1)Assumethesteadystateoutputis:xss=Asin(10t+θ)Dxss=10Acos(10t+θ),D2xss=-100Asin(10t+θ),D3xss=-1000Acos(10t+θ...