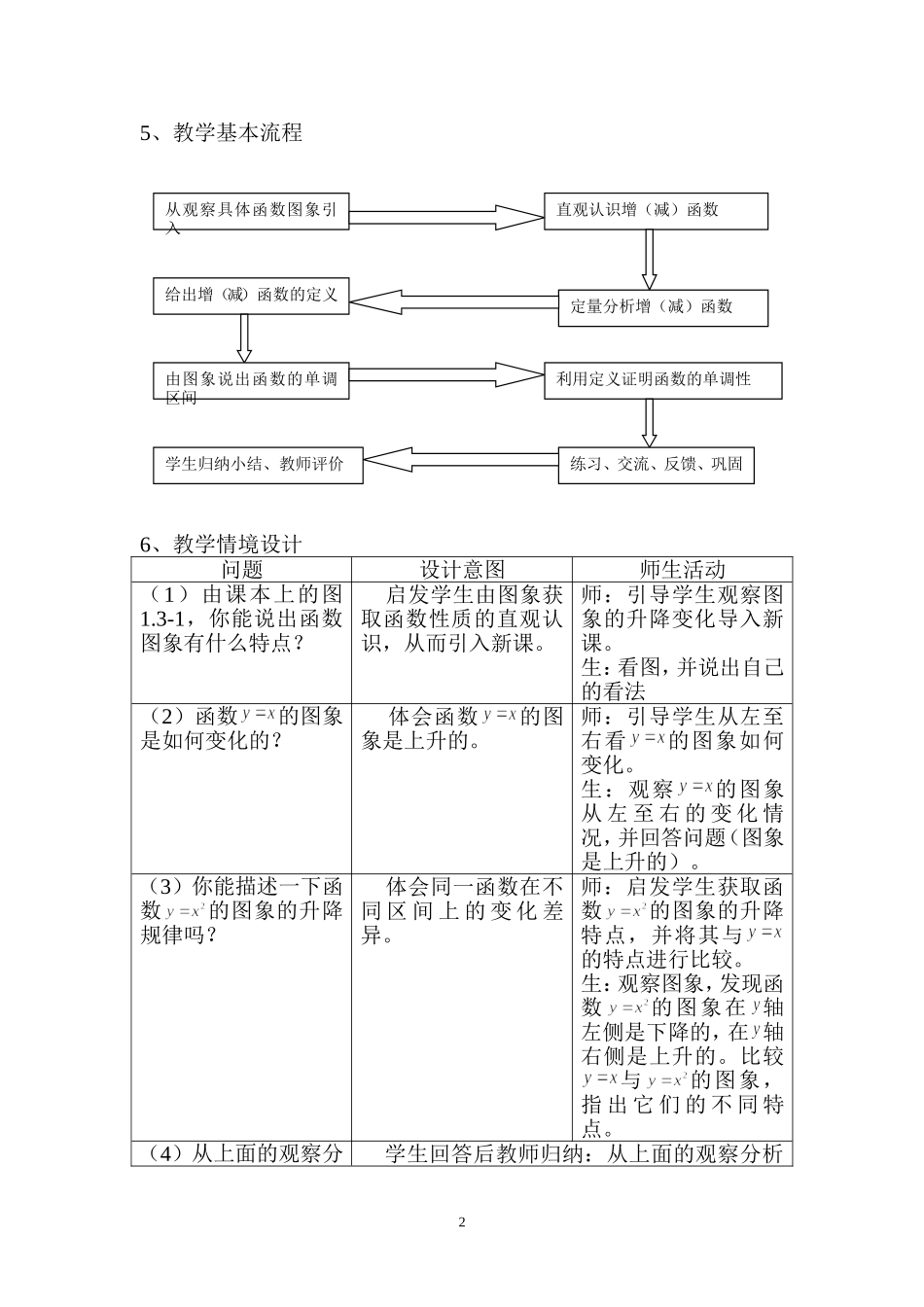
课题:函数的单调性(第一课时)1、教学任务分析(1)建立增(减)函数的概念。通过观察一些函数图象的升降,形成增(减)函数的直观认识。再通过具体函数值的大小比较,认识函数值随自变量的增大而增大(减小)的规律,由此得出增(减)函数的定义。掌握用定义证明函数单调性的基本方法与步骤。(2)函数的单调性的研究经历了从直观到抽象,从图形语言到数学语言,理解增函数、减函数、单调区间概念的过程,在这个过程中,让学生通过自主探究活动,体验数学概念的形成过程,使学生学习数学思考的基本方法,培养学生的数学思维能力。2、教学目标(1)、知识与技能:使学生理解函数单调性的概念,初步掌握判别函数单调性的方法;(2)、过程与方法:引导学生通过观察、归纳、抽象、概括,自主建构单调增函数、单调减函数等概念;能运用函数单调性概念解决简单的问题;使学生领会数形结合的数学思想方法,培养学生发现问题、分析问题、解决问题的能力.(3)、情感、态度与价值观:在函数单调性的学习过程中,使学生体验数学的科学价值和应用价值,培养学生善于观察、勇于探索的良好习惯和严谨的科学态度.3、教学重点、难点重点:形成增(减)函数的形式化定义。难点:形成增(减)函数概念的过程中,如何从图象升降的直观认识过渡到函数增减的数学符号语言表述;用定义证明函数的单调性。4、学法与教法学法:(1)合作学习:引导学生分组讨论,合作交流,共同探讨问题(2)自主学习:引导学生通过亲身经历,动口、动脑、动手参与数学活动(3)探究学习:引导学生发挥主观能动性,主动探索新知(如例题的处理)。教学用具:电脑、多媒体。教法:整堂课围绕“一切为了学生发展”的教学原则突出:①动——师生互动、共同探索;②导——教师指导、循序渐进。(1)新课引入——提出问题,激发学生的求知欲。(2)理解导数的内涵——数形结合,动手计算,组织学生自主探索,获得函数单调性的定义。(3)例题处理——始终从问题出发,层层设疑,让他们在探索中自得知识。(4)变式练习——深化对函数单调性内涵的理解,巩固新知。15、教学基本流程6、教学情境设计问题设计意图师生活动(1)由课本上的图1.3-1,你能说出函数图象有什么特点?启发学生由图象获取函数性质的直观认识,从而引入新课。师:引导学生观察图象的升降变化导入新课。生:看图,并说出自己的看法(2)函数的图象是如何变化的?体会函数的图象是上升的。师:引导学生从左至右看的图象如何变化。生:观察的图象从左至右的变化情况,并回答问题(图象是上升的)。(3)你能描述一下函数的图象的升降规律吗?体会同一函数在不同区间上的变化差异。师:启发学生获取函数的图象的升降特点,并将其与的特点进行比较。生:观察图象,发现函数的图象在轴左侧是下降的,在轴右侧是上升的。比较与的图象,指出它们的不同特点。(4)从上面的观察分学生回答后教师归纳:从上面的观察分析从观察具体函数图象引入直观认识增(减)函数定量分析增(减)函数给出增(减)函数的定义由图象说出函数的单调区间利用定义证明函数的单调性练习、交流、反馈、巩固学生归纳小结、教师评价2析,能得出什么结论?可以看出:不同的函数,其图象的变化趋势不同,同一函数在不同的区间上的变化趋势也不同。函数图象的这种变化规律就是函数性质的反映。这就是我们今天所要研究的函数的一个重要性质——函数的单调性(引出课题)。(5)函数的图象在轴右侧是上升的,如何用数学符号语言来描述这种“上升”呢?指导学生从定性分析到定量分析,从直观认识过渡到数学符号表述。师:指导学生完成的对应值表1.3-1,并观察表格中,自变量的值从0到5变化时,函数值如何变化。生:填表并回答问题(自变量的值增大,函数值增大)。师:在上,任意改变,的值,当时,都有吗?生:随意给出一些上的,的值,当时,验证是否都有。师:由此你能得出什么结论?生:表述各自的结论。师:对学生得出的结论给予评价,然后提出:刚才我们所验证的是一些具体的、有限个自变量的值,对于上任意的,,当时,是否都3有呢?生:思考如何验证老师提出的问题,并将自己的想法与同...