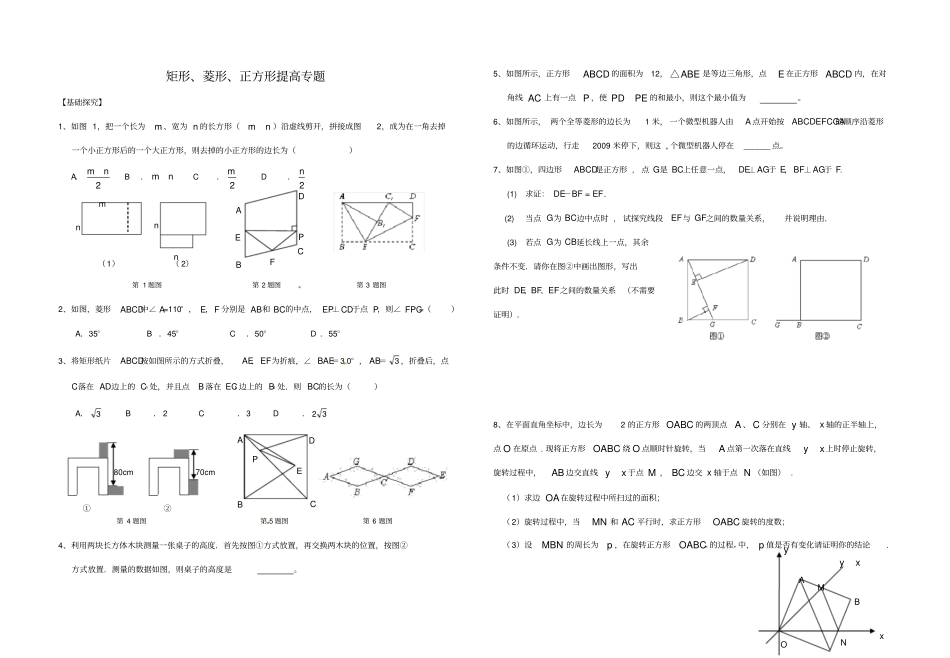
矩形、菱形、正方形提高专题【基础探究】1、如图1,把一个长为m、宽为n的长方形(mn)沿虚线剪开,拼接成图2,成为在一角去掉一个小正方形后的一个大正方形,则去掉的小正方形的边长为()A.2mnB.mnC.2mD.2n第1题图第2题图第3题图2、如图,菱形ABCD中∠A=110°,E,F分别是AB和BC的中点,EP⊥CD于点P,则∠FPC=()A.35°B.45°C.50°D.55°3、将矩形纸片ABCD按如图所示的方式折叠,AE、EF为折痕,∠BAE=30°,AB=3,折叠后,点C落在AD边上的C1处,并且点B落在EC1边上的B1处.则BC的长为()A.3B.2C.3D.32第4题图第5题图第6题图4、利用两块长方体木块测量一张桌子的高度.首先按图①方式放置,再交换两木块的位置,按图②方式放置.测量的数据如图,则桌子的高度是。5、如图所示,正方形ABCD的面积为12,ABE△是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PDPE的和最小,则这个最小值为。6、如图所示,两个全等菱形的边长为1米,一个微型机器人由A点开始按ABCDEFCGA的顺序沿菱形的边循环运动,行走2009米停下,则这个微型机器人停在______点。7、如图①,四边形ABCD是正方形,点G是BC上任意一点,DE⊥AG于E,BF⊥AG于F.(1)求证:DE-BF=EF.(2)当点G为BC边中点时,试探究线段EF与GF之间的数量关系,并说明理由.(3)若点G为CB延长线上一点,其余条件不变.请你在图②中画出图形,写出此时DE、BF、EF之间的数量关系(不需要证明).8、在平面直角坐标中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线yx上时停止旋转,旋转过程中,AB边交直线yx于点M,BC边交x轴于点N(如图).(1)求边OA在旋转过程中所扫过的面积;(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;(3)设MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化请证明你的结论.ADEPBCOABMNyxxymnnn(2)(1)ADEPCBF80cm①70cm②9、如图①,正方形ABCD中,点A、B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D匀速运动,同时动点Q以相同速度在x轴上运动,当P点到D点时,两点同时停止运动,设运动的时间为t秒.(1)当P点在边AB上运动时,点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;(2)求正方形边长及顶点C的坐标;(3)在(1)中当t为何值时,△OPQ的面积最大,并求此时P点的坐标.【综合探究】10、在边长为6的菱形ABCD中,动点M从点A出发,沿A→B→C向终点C运动,连接DM交AC于点N.(1)如图1,当点M在AB边上时,连接BN.①求证:ABNADN△≌△;②若∠ABC=60°,AM=4,∠ABN=,求点M到AD的距离及tan的值;(2)如图2,若∠ABC=90°,记点M运动所经过的路程为x(6≤x≤12).试问:x为何值时,△ADN为等腰三角形.11、如图①,已知两个菱形ABCD和EFGH是以坐标原点O为位似中心的位似图形(菱形ABCD与菱形EFGH的位似比为2︰1),∠BAD=120°,对角线均在坐标轴上,抛物线213yx经过AD的中点M.⑴填空:A点坐标为,D点坐标为;⑵操作:如图②,固定菱形ABCD,将菱形EFGH绕O点顺时针方向旋转度角(090),并延长OE交AD于P,延长OH交CD于Q.探究1:在旋转的过程中是否存在某一角度,使得四边形AFEP是平行四边形若存在,请推断出的值;若不存在,说明理由;探究2:设AP=x,四边形OPDQ的面积为s,求s与x之间的函数关系式,并指出x的取值范围.12、如图1,正方形ABCD和正方形QMNP,∠QMN=∠ABC,M是正方形ABCD的对角线AC、BD的交点,MN交AB于F,QM交AD于E.(1)线段ME与线段MF的大小关系是:ME______MF(填“<”、“=”、“>”)(不必说明理由).(2)如图2,若将原题中的“正方形”改为“菱形”,其他条件不变,探索线段ME与线段MF的xyOMHGFEDCBA图①HGFEDCBA图②xyOQPCBMAND(图1)CMBNAD(图2)大小关系,并加以证明.(3)如图3,若将原题中的“正方形”改为“矩形”,且BC=2AB,其他条件不变,探索线段ME与线段MF的大小关系,并说明理由.(4)根据前面的探索和图4,若将原题中的“正方形”改为“平行四边形”,且BC=kAB(k是常数,且k>1),其他条件不变,则ME与MF的大小关系又如何呢请写出结论并加以说明.BCADEMPQFN图4FABCDMNPQE图3MABCDEFNPQ图1AEDCBMNQPF图2