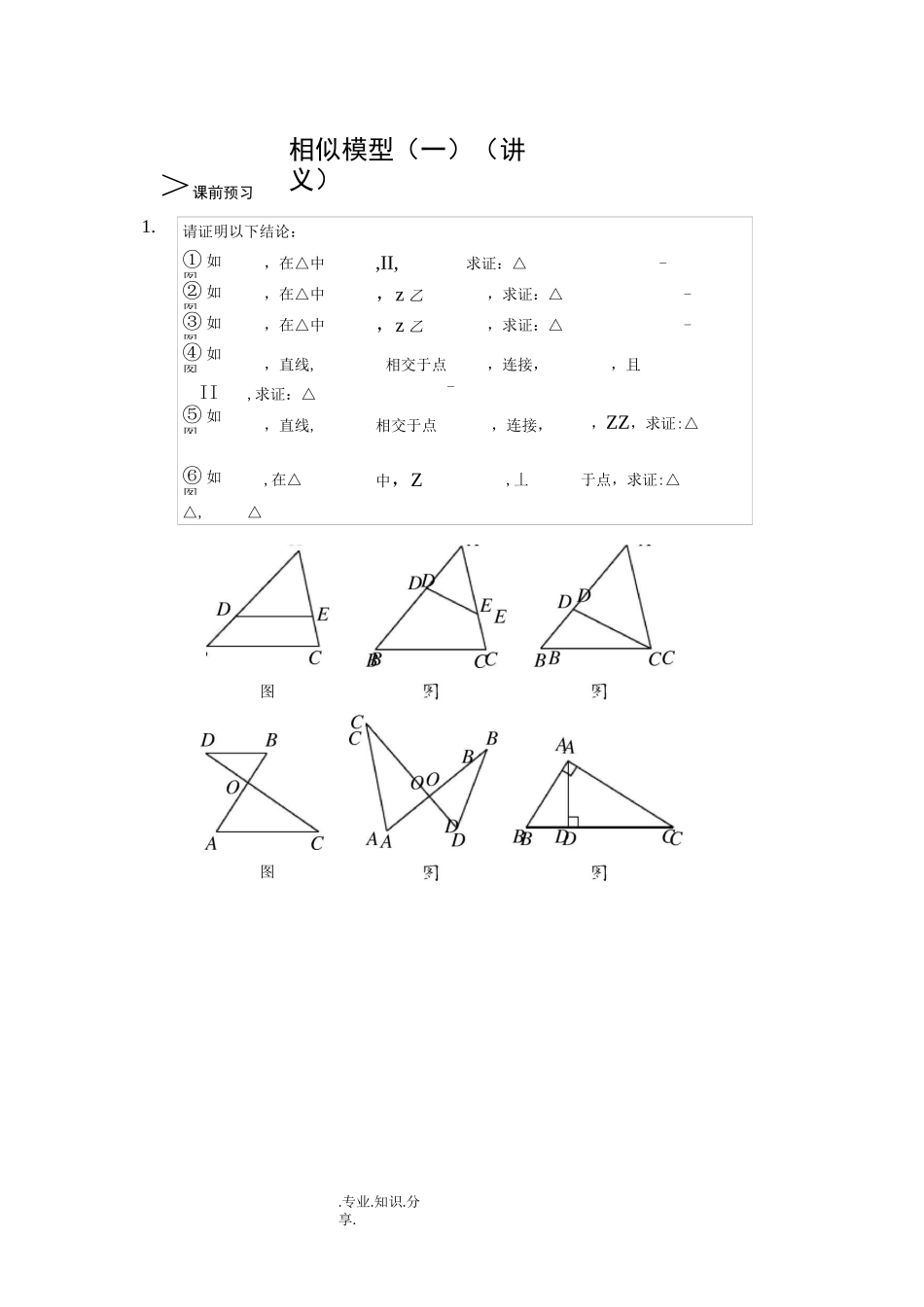
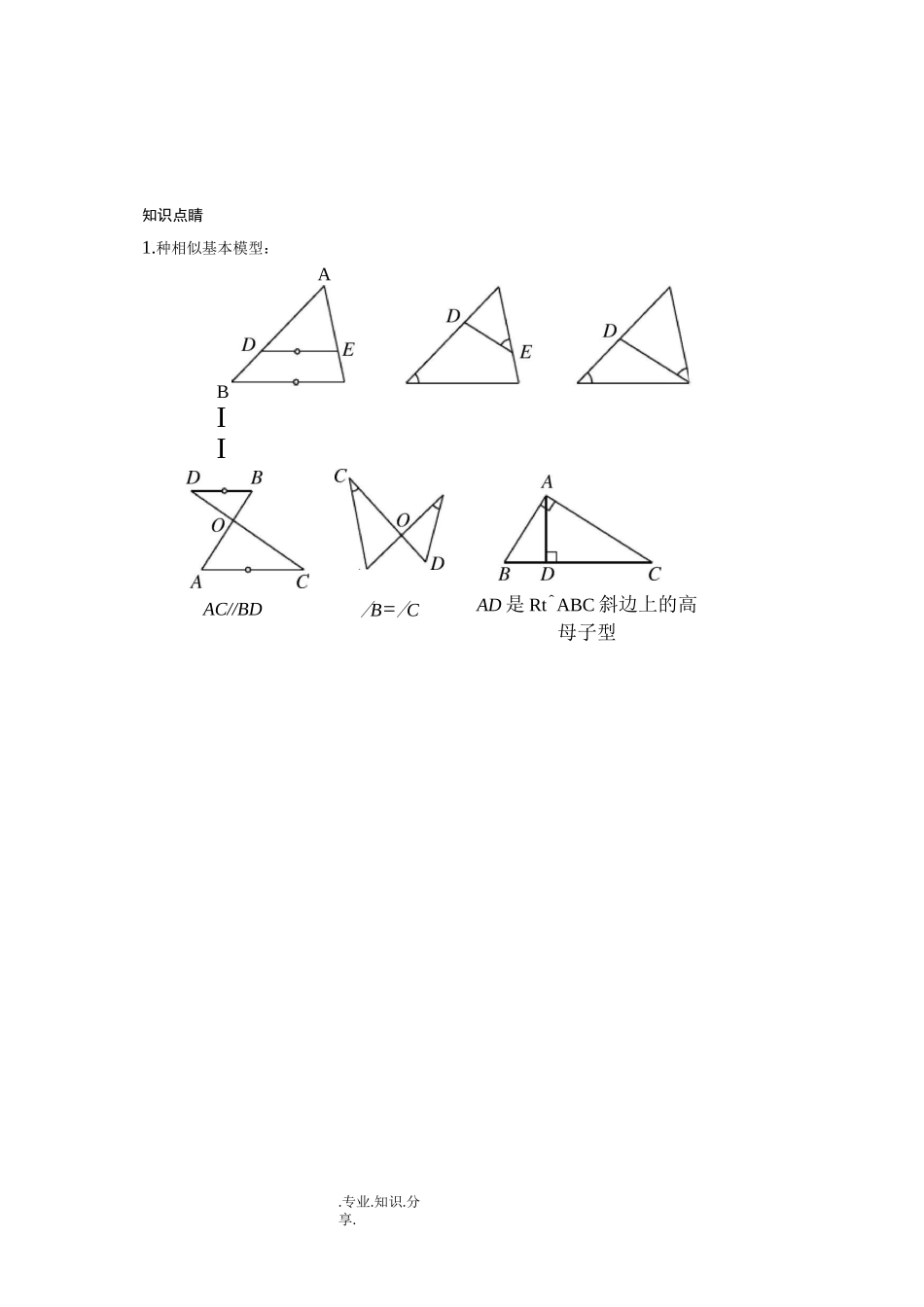
.专业.知识.分享.相似模型(一)(讲义)>课前预习1.请证明以下结论:①如图,在△中,II,求证:△-②如图,在△中,z乙,求证:△-③如图,在△中,z乙,求证:△-④如图,直线,相交于点,连接,,且II,求证:△-⑤如图,直线,相交于点,连接,,ZZ,求证:△⑥如图,在△中,Z,丄于点,求证:△△,△图图.WORD.格式整理..专业.知识.分享..专业.知识.分享.知识点睛1.种相似基本模型:ABIIAC//BD/B=/CAD是Rt^ABC斜边上的高母子型.WORD.格式整理..专业.知识.分享.种常见处方式.专业.知识.分享.、是影'子J•墙时的三它们的实质是构造三角形相似7•△DEHS^ABC2.影子上墙:H.WORD.格式整理..专业.知识.分享.EF△DHGS^ABC△HEFS^ABC1.如图,2.3.CD_~BC~9其中则99△,丄-于点,如图,在如图,在同一平面内公共顶点,zz将两个全等的等腰直角三角形,它们的斜边长为•△第是线段题图上一点且满足和摆放在-起,为固定动,△绕点.WORD•格式整理..专业.知识.分享.旋转,与边的交点分别为,(点与点重合,点与点重合)-①请写出图中所有的相似三角形②=2,则=4.如图,为线段上一点,与交于点,乙二乙=z=a,且()写出图中的三对相似三角形;△•、②△与△③厶与△•其中相似的有(填写序号)•.WORD.格式整理..专业.知识.分享..WORD•格式整理..专业.知识.分享.6.且zDCB=zA,BDCD=789B-35C-3△ABD中,过点D作CD丄BD,垂足为D,连接BC交AD于0,则B=AB=,CD如图则B第题图,在□ABCD中=B,BCC,AC,分别交BD于,10分别与AD,BD交于点BFFCBF.WORD.格式整理..专业.知识.分享.如图,在△ABC中,zACB=90,丄AB于点,D在AB的延长线上‘AE=▲£,则ABCD的面积是()如图,在I—ABCD中,是BA延长线上一点,CEGAGEF-则下结论:①—=—;②—=GCGDFCFD如图,在9第9题图BC的中点,连接A9l如图,直线||D题图第,则CA=.WORD•格式整理..专业.知识.分享..WORD.格式整理..专业.知识.分享.14C题图和地面J■,得16.如图,中,为的延长线于点-17.如图,在等腰三角形CDB3底边米,米,与地面成30角,且此时测得米杆的影长为米,则电线杆的高为()-米-米-(7+>/3)米-(14+2馆)米15.如图,在斜坡的顶部有一铁塔,是的中点,是水平的,在阳光的照射下,塔影在坡面上-铁塔底座宽,塔影长,小明和小华的身高是,同一时刻小明站在点处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为和,则塔高为(:---0-第在土坡的坡面麺90.WORD.格式整理..专业.知识.分享.如口图,在I—ABCD中,是AD延长线上一点,B分别与AC,CD交于点,,求证:AE-CF=BC-AB-.WORD.格式整理..专业.知识.分享..WORD.格式整理..专业.知识.分享..WORD.格式整理..专业.知识.分享..WORD.格式整理..专业.知识.分享.【参考答案】>知识点睛角相等、比线段;比的传递与整合;比推墙法;抬高地面法;砍树法框内答案框:AC2=BC-CD;AD2=CD•DB-讲练.3;—410T;4\厅;2、岳①厶,△丸2②3()△s△,△S△,△S△;()证明-①②③①②③④①②③④证明-米