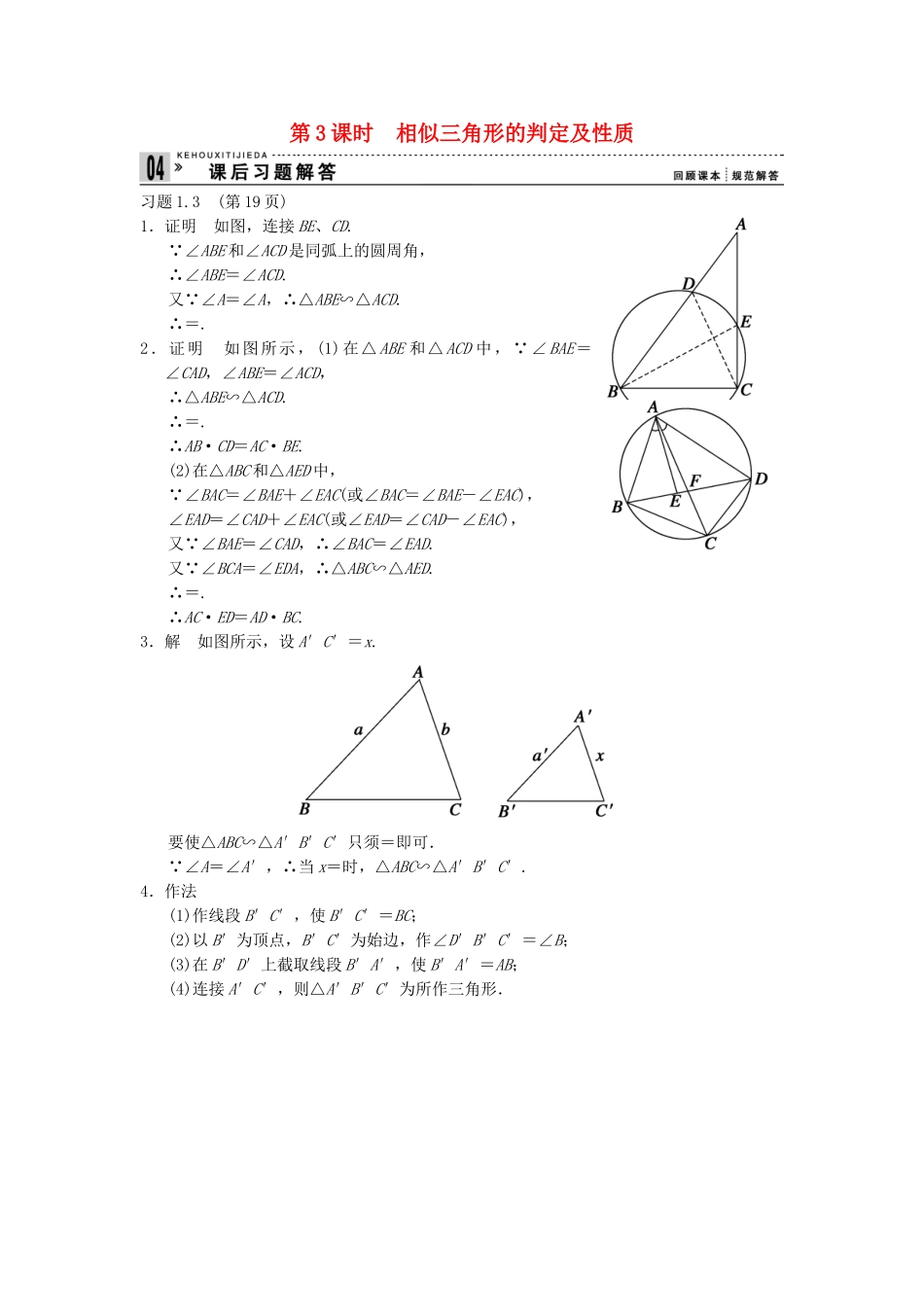
第3课时相似三角形的判定及性质习题1.3(第19页)1.证明如图,连接BE、CD.∵∠ABE和∠ACD是同弧上的圆周角,∴∠ABE=∠ACD.又∵∠A=∠A,∴△ABE∽△ACD.∴=.2.证明如图所示,(1)在△ABE和△ACD中,∵∠BAE=∠CAD,∠ABE=∠ACD,∴△ABE∽△ACD.∴=.∴AB·CD=AC·BE.(2)在△ABC和△AED中,∵∠BAC=∠BAE+∠EAC(或∠BAC=∠BAE-∠EAC),∠EAD=∠CAD+∠EAC(或∠EAD=∠CAD-∠EAC),又∵∠BAE=∠CAD,∴∠BAC=∠EAD.又∵∠BCA=∠EDA,∴△ABC∽△AED.∴=.∴AC·ED=AD·BC.3.解如图所示,设A′C′=x.要使△ABC∽△A′B′C′只须=即可.∵∠A=∠A′,∴当x=时,△ABC∽△A′B′C′.4.作法(1)作线段B′C′,使B′C′=BC;(2)以B′为顶点,B′C′为始边,作∠D′B′C′=∠B;(3)在B′D′上截取线段B′A′,使B′A′=AB;(4)连接A′C′,则△A′B′C′为所作三角形.5.证明∵EF∥AD∥BC,∴=,=.∵AD=BC,∴=.∴=.又∵∠AEB=∠HEG,∴△AEB∽△HEG.∴∠ABE=∠HGE.∴GH∥AB.6.证明∵DE∥AB,∴==.①又∵EF∥BC,∴==.②∴=.由①、②知=,而∠FOD=∠COA,∴△FOD∽△COA.∴=.∴在△ABC和△DEF中,有==.∴△ABC∽△DEF.7.证明在△ACD和△BCE中,∵∠ADC=∠BEC=90°,∠ACD=∠BCE,∴△ACD∽△BCE.∴=,即AD·BC=BE·AC.8.解方案1:(1)在地面适当位置选取一点C,连接BC,测量出BC的距离;(2)在点C竖立一根垂直于地面的标尺杆;(3)在BC的延长线上取一点D,使点D、标尺杆的顶点E和树尖在一条直线上;(4)测量CD的距离.在这个方案中,由于△DCE∽△DBA,而BC、CD、CE的长可以由测量而得,所以可以求出树高AB的长.(没有考虑测量仪的脚架高)方案2:(1)在地面上选取一点C,连接BC;(2)测出∠BCA;(3)在地面上选取一点D,使∠DCB=∠BCA;(4)过D作BC的垂线,交BC于E;(5)测量DE、CE、BC的长,由这三个量可以求得AB的长.因为按方案2的实施,易知Rt△ABC∽Rt△DEC.(没有考虑测量仪的脚架高)方案3:(1)把一面镜子放在离树a米的点E;(2)一个人望着镜子后退到点D,这时恰好在镜子里望到树梢点A;(3)量得ED为b米,人的眼睛距地面的高度为c米,即可求AB的长.因为根据光学中的反射定律,知∠AEB=∠CED,所以△ABE∽△CDE.9.证明如图所示,设△ABC∽△A′B′C′,相似比为k.(1)设AD是△ABC中BC边上的中线,A′D′是△A′B′C′中B′C′边上的中线.∵△ABC∽△A′B′C′,∴=.又∵D、D′分别为BC、B′C′的中点,∴===.又∵∠B=∠B′,∴△ABD∽△A′B′D′.∴==k.其余两组对应中线之比同理可证.(2)设AE、A′E′分别是△ABC、△A′B′C′中∠A和∠A′的内角平分线.∵△ABC∽△A′B′C′,∴∠BAC=∠B′A′C′,∠B=∠B′.∴∠BAE=∠B′A′E′.∴△ABE∽△A′B′E′.∴==k.同理可证,其余两个对应角的内角平分线之比也等于相似比.10.解在△AEF和△CDF中,∵∠DCF=∠EAF,∠DFC=∠EFA,∴△AEF∽△CDF.∴==.∴=k2=.而S△AEF=6,∴S△CDF=9S△AEF=9×6=54(cm2).11.解问题1:相似三角形对应角的外角平分线之比等于相似比.证明:设△ABC∽△A′B′C′.AD、A′D′分别是∠A、∠A′的外角平分线,分别交BC、B′C′的延长线于D、D′.∵△ABC∽△A′B′C′,∴∠BAC=∠B′A′C′.又∵∠BAC+∠1+∠2=∠B′A′C′+∠3+∠4,而∠1=∠2,∠3=∠4,∴∠1=∠3.∴∠BAD=B′A′D′.又∵∠B=∠B′,∴△ABD∽△A′B′D′.∴==k.问题2:△ABC∽△A′B′C′,以△ABC的三条边为直径,分别向△ABC外作半圆(如图所示),同样,以△A′B′C′的三条边为直径,分别向△A′B′C′外作半圆.则两个三角形中三个对应半圆的面积之比等于相似比的平方.说明将三个半圆改为三个等边三角形、正方形、正多边形等,可以得到更多的命题.问题3:如图所示,△ABC∽△A′B′C′,相似比为k,=.则=k.说明该题是一个开放型问题,可以由联想、类比等方法得到许多新问题.在教学中应引导、启发和鼓励学生去探究、猜想.